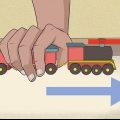
Glem heller ikke at forbinde startpunktet med slutpunktet ved hjælp af en lige linje.Dette er den forskydning, vi skal beregne. For eksempel, hvis en genstand først bevæger sig 300 meter i østlig retning og derefter 400 meter i nordlig retning, dannes en retvinklet trekant. AB er den første side og BC er den anden side af trekanten.AC er trekantens hypotenus, og dens værdi er objektets forskydning. I dette eksempel er de to retninger "øst" og "nord." 
For eksempel er x = 300 og y = 400.Din ligning ser nu sådan ud: s = √300² + 400². 
For eksempel: s = √90000 + 160000.s = √250000.s = 500.Du ved nu, at forskydningen er lig med 500 meter. 

Ligningen vil se sådan ud: s = 1/2(20 + 23)45. 
For denne ligning betyder det ikke meget, hvis du ved et uheld skifter start- og sluthastigheden. Fordi du tilføjer disse værdier sammen først, er det lige meget. Men i andre ligninger kan udskiftning af start- og sluthastigheden påvirke det endelige svar eller værdien af forskydningen. Din ligning ser nu sådan ud: s = 1/2(43)45.Del først 43 med 2, hvilket giver 21,5 som svar. Gang 21,5 med 45, hvilket giver 967,5 meter som svar.967,5 er bilens slagvolumen, set fra udgangspunktet. 

Baseret på eksemplet ovenfor skulle din ligning nu se sådan ud: s = 25(4) + 1/2(3)4².Det kan helt sikkert hjælpe, hvis du sætter parenteser omkring accelerations- og tidsværdierne for at holde tallene adskilt fra hinanden. 
Lad os se nærmere på ligningen: s = 25(4) + 1/2(3)4². Rækkefølgen er: 4² = 16; derefter 16 x 3 = 48; derefter 25 x 4 = 100; og hvis sidst 48/2 = 24. Ligningen ser nu sådan ud: s = 100 + 24.Efter addition giver dette s = 124, så forskydningen er 124 meter. 

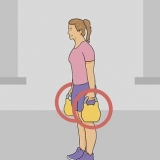
Et eksempel på en opgave: En pige sidder på en karusell. Hendes sæde er i en afstand af 1 meter fra centrum af cirklen (radius). Hvis pigen bevæger sig langs en 1,5 meter cirkulær bue (lineær forskydning), hvad er hendes vinkelforskydning? Ligningen ser således ud: θ = 1,5/1. 
Efter division 1,5/1 står du tilbage med 1,5.Pigens vinkelforskydning er 1,5 radianer. Da vinkelforskydning angiver, hvor meget et objekt er blevet roteret fra sin udgangsposition, er det nødvendigt at repræsentere dette i radianer, ikke som en afstand. Radianer er enheder, der bruges til at måle vinkler. 

Forskydning kaldes også en "vektor mængde" omtales som ændringen i et objekts position sammenlignet med den retning, objektet bevæger sig i. Antag, at du går 5 meter mod øst. Går du 5 meter mod vest igen, bevæger du dig i den modsatte retning, tilbage til dit udgangspunkt. Selvom du har gået i alt 10 meter, har din position ikke ændret sig, og din forskydning er derfor 0 meter. 
Forestil dig en fodboldtræner, der hopper frem og tilbage langs sidelinjen.Mens han har givet anvisninger til spillerne, har han gået ned ad linjen flere gange, frem og tilbage. Hvis du konstant ville holde øje med træneren, ville du se den afstand, han tilbagelægger. Men antag, at træneren stopper for at sige noget til en forsvarsspiller? Hvis han er et sted, der er anderledes end hans udgangspunkt, så ser du på trænerens bevægelse (på et bestemt tidspunkt). 
En buet sti vil til sidst føre dig fra startpunkt til slutpunkt, men dette er ikke den korteste vej. For at hjælpe dig med at visualisere dette, forestil dig at gå i en lige linje og blive stoppet af en søjle eller en anden forhindring. Du kan ikke gå gennem søjlen, så du går rundt om den. Selvom man ender samme sted, som hvis man var gået lige igennem søjlen, skulle man alligevel rejse en længere vej for at komme dertil. Selvom forskydningen fortrinsvis er i en lige linje, er det muligt at måle forskydningen af et objekt, der "godt" bevæger sig ad en kroget sti. Dette kaldes "vinkelforskydning" og det kan beregnes ved at finde den korteste afstand, der findes mellem startpunkt og slutpunkt. 
Antag for eksempel, at du går 5 meter mod øst og derefter 3 meter mod vest. Selvom du teknisk set er 2 meter væk fra dit udgangspunkt, er forskydningen -2, fordi du bevæger dig i den modsatte retning på det punkt.Afstanden vil altid være positiv, fordi du ikke kender en distance, du har tilbagelagt "fortrydes" kan lave. Negativ forskydning betyder ikke, at forskydningen falder. Det er simpelthen en måde at indikere, at bevægelsen er i den modsatte retning. 
Det er altså kun muligt, hvis du bevæger dig i en lige linje fra udgangspunktet, og uden at ændre retning bagefter.Antag for eksempel, at du bor i San Francisco, Californien, og får et job i Las Vegas, Nevada. Du bliver så nødt til at flytte til Las Vegas for at bo tættere på arbejdet. Hvis du tager flyet, et direkte fly fra San Francisco til Las Vegas, har du rejst 670 km, og din deplacement er derfor 670 km. Men hvis du rejser i bil fra San Francisco til Las Vegas, kan din afstand stadig være 670 km, men du har rejst 906 km i mellemtiden.Da kørsel normalt indebærer en retningsændring (slå fra, tage en anden rute), har du kørt meget længere end den korteste afstand mellem de to byer.
Beregn forskydning
Indhold
Udtrykket forskydning i fysik refererer til ændringen snarere end et objekt. Ved beregning af forskydning måler man, hvor meget et objekt har bevæget sig, baseret på data fra startposition og slutposition. Formlen du bruger til at bestemme forskydningen afhænger af de variabler, der er givet for et problem. Tag følgende trin for at lære, hvordan man beregner forskydningen af et objekt.
Trin
Del 1 af 5: Beregning af den resulterende forskydning

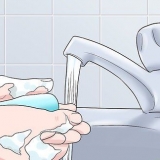
1. Brug formlen for den resulterende forskydning ved at bruge den længdeenhed, der bruges til at angive start- og slutpositionen. Mens afstand er forskellig fra forskydning, vil en erklæring om resulterende forskydning angive, hvor meget "måler" har kasseret en genstand. Brug disse måleenheder til at beregne forskydningen, hvor langt et objekt er fra dets oprindelige placering.
- Ligningen for den resulterende forskydning er: s = √x²+y²."s" står for forskydning.X er den første retning, objektet bevæger sig, og y er den anden retning, objektet bevæger sig. Hvis dit objekt kun bevæger sig i 1 retning, så er y = 0.
- Et objekt kan kun bevæge sig i maks. 2 retninger, fordi bevægelse langs nord-syd-linjen eller øst-vest-linjen betragtes som neutral.

2. Forbind prikkerne i overensstemmelse med bevægelsesrækkefølgen og mærk disse prikker fra A-Z.Brug en lineal til at tegne lige linjer fra punkt til punkt.

3. Indtast værdierne for x² og y².Nu hvor du ved i hvilken retning dit objekt bevæger sig, kan du begynde at udfylde værdierne for de relevante variabler.

4. Udregn ligningen. Beregn først 300² og derefter 400², læg dem sammen og træk kvadratroden af summen fra.
Del 2 af 5: At kende hastighedsvektoren og tidens varighed

1. Brug denne formel, hvis opgaven giver hastighedsvektoren og tidens varighed. Det kan ske, at et fysikproblem ikke siger et ord om den tilbagelagte afstand, men angiver, hvor længe et objekt har rejst og med hvilken hastighed. Du kan derefter beregne forskydningen ved hjælp af tidsvarighed og hastighed.
- I dette tilfælde vil ligningen se sådan ud: s = 1/2(u + v)t.u = objektets begyndelseshastighed, den hastighed, hvormed objektet begyndte at bevæge sig i en bestemt retning.v = objektets sluthastighed, eller hvor hurtigt det gik til sidst. t = den tid, det tog objektet at nå sin destination.
- For eksempel: En bil kører i 45 sekunder.Bilen drejede mod vest med en hastighed på 20 m/s (starthastighed) og for enden af gaden er hastigheden 23 m/s (sluthastighed). Beregnet forskydningen baseret på disse data.

2. Indtast værdierne for hastighed og tid. Nu hvor du ved, hvor længe bilen har kørt, og hvad start- og sluthastigheden var, kan du finde afstanden fra startpunktet til slutpunktet.

3. Udregn ligningen, når du har indtastet værdierne. Husk at beregne vilkårene i den rigtige rækkefølge, ellers går forskydningen galt.
Del 3 af 5: Når hastighed, acceleration og tid er angivet

1. En anden ligning er nødvendig, hvis accelerationen er givet for et problem, sammen med hastigheden og tiden. Med sådan en opgave ved du, hvad objektets begyndelseshastighed har været, hvad accelerationen er, og hvor længe objektet har været på vejen. Du skal bruge følgende ligning.
- Ligningen for denne type problem ser således ud: s = ut + 1/2at².Det "du" repræsenterer stadig starthastigheden; Det "-en" er objektets acceleration, eller også hvor hurtigt objektets hastighed ændres. Variablen"t" kan enten betyde den samlede tid, eller det kan angive en bestemt periode, hvor objektet har accelereret. Under alle omstændigheder er dette angivet i tidsenheder som sekunder, timer osv.
- Antag, at en bil med en starthastighed på 25 m/s får en acceleration på 3 m/s2 i en periode på 4 sekunder.Hvad er forskydningen af bilen efter 4 sekunder?

2. Udfyld værdierne på det rigtige sted i ligningen. I modsætning til den foregående ligning vises kun starthastigheden her, så sørg for at indtaste de korrekte værdier.

3. Beregn forskydningen ved at løse ligningen. En hurtig måde at hjælpe dig med at huske rækkefølgen af operationer i en ligning er mnemonikken "Mr. Dale venter på svar".Angiver alle aritmetiske operationer i den rigtige rækkefølge (overdrivelse, multiplikation, division, kvadrering, addition og subtraktion).
Del 4 af 5: Beregning af vinkelforskydningen

1. Bestemmelse af vinkelforskydningen, når et objekt bevæger sig langs en kurve. Selvom dette stadig involverer beregning af forskydningen ved hjælp af en lige linje, har du brug for forskellen mellem start- og slutposition langs en buet bane.
- Tag som eksempel en pige, der er på karuseller. Mens hun snurrer rundt om ydersiden af hjulet, bevæger hun sig i en cirkel. Vinkelforskydning forsøger at finde den korteste afstand mellem start- og slutposition, hvis en genstand ikke bevæger sig i en lige linje.
- Formlen for vinkelforskydningen er: θ = S/r, hvorved "s" står for den lineære forskydning, "r" for radius, og "θ" vinkelforskydningen er.Lineær forskydning er den afstand et objekt rejser langs en cirkel.Radius er afstanden af et objekt fra centrum af cirklen.Vinkelforskydning er værdi, vi gerne vil vide.

2. Sæt værdierne af den lineære forskydning og radius ind i ligningen. Husk at radius er afstanden fra midten af en cirkel til kanten; det kan være, at diameteren er givet for et problem, i så fald skal du dividere det med 2 for at finde radius (radius) af cirklen.

3. Divider den lineære forskydning med radius.Dette vil give dig vinkelforskydningen af objektet.
Del 5 af 5: Forståelse af forskydning

1. Det er vigtigt at forstå det "afstand" nogle gange betyder noget andet end "forskydning."Afstand siger noget om, hvor langt en genstand har bevæget sig i alt.
- Afstand er noget vi også kalder en "skalar" at nævne. Det er en måde at angive, hvor lang afstand du har tilbagelagt, men siger intet om den retning, du har bevæget dig.
- Hvis du for eksempel går 2 meter mod øst, 2 meter mod syd, 2 meter mod vest og igen 2 meter mod nord, er du tilbage ved dit udgangspunkt. Selvom du har tilbagelagt en samlet distance på 10 meter, er din forskydning lig med 0 meter, fordi dit slutpunkt er lig med dit startpunkt.

2. Forskydning er forskellen mellem to punkter. Forskydning er ikke en sum af bevægelser, som det er tilfældet med afstand; det handler kun om delen mellem dit start- og dit slutpunkt.

3. Husk ordene godt "frem og tilbage" når du prøver at forestille dig en forskydning. Den modsatte retning fortryder bevægelsen i den oprindelige retning.

4. Forskydningen måles langs en lige linje, ikke langs en cirkulær bane. For at finde ud af bevægelsen leder du efter den korteste vej mellem to forskellige punkter.

5. Forstå venligst, at forskydning også kan have en negativ værdi i modsætning til afstand. Hvis slutpunktet nås ved at bevæge dig i en retning modsat den retning, du startede (i forhold til startpunktet), så er din forskydning negativ.

6. Indse, at afstands- og forskydningsværdierne nogle gange kan være de samme. Hvis du går lige 25 meter og derefter stopper, er afstanden du har tilbagelagt lig med forskydningen, simpelthen fordi du ikke har ændret retning.
Tips
- Arbejd præcist
- Husk ikke formlerne udenad, men prøv at forstå, hvordan de virker
Fornødenheder
- Lommeregner
- Afstandsmåler
Artikler om emnet "Beregn forskydning"
Оцените, пожалуйста статью
Populær