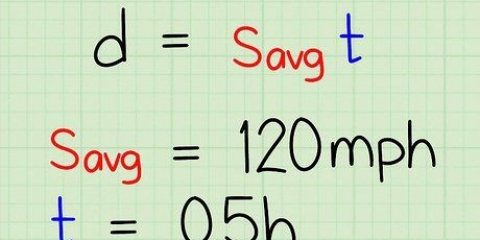Afstanden skal vises i meter (SI-enhed). I vores eksempel med toget bestemmer vi det arbejde, der udføres på toget, når det bevæger sig langs sporet. Hvis startpunktet er sat til 0, og slutpunktet til 2 meter, så siger vi, at forskydningen D er lig med 2 meter. 
Bemærk, at kraftenheden er Newton. Antag, at vi ikke kender størrelsen af kraften i dette eksempel. Men vi ved, at togets masse er lig med 0,5 kg, og at kraften får det til at accelerere med 0,7 m/s. I dette tilfælde kan vi finde størrelsen ved at bruge M x A = 0,5 x 0,7 = 0,35 Newton. 
Nu er det tid til at løse det faktiske problem. Med en værdi for kraften på 0,35 Newton og en værdi for forskydningen på 2 meter bliver svaret: 0,35 × 2 = 0,7 joule. Du har måske bemærket, at der i formlen som angivet i introen er en ekstra del: cos(θ). Som nævnt ovenfor er kraften og retningen af bevægelsen den samme. Det betyder, at vinklen mellem dem er lig med 0. Da cos(0) = 1, behøver vi ikke vinklen, fordi den er lig med 1. 
Bemærk, at der er et alternativt udtryk for joule; 1 watt i sekundet. Se nedenfor for en nærmere behandling af magt i forhold til arbejde. 

I vores eksempelopgave siger vi, at kraften påføres fra en vinkel på 60 grader fra vandret. Hvis toget stadig bevæger sig vandret, så er vinklen mellem togets forskydning og kraften lig med 60. 
Lad os nu løse prøveproblemet. Ved hjælp af en lommeregner bestemmer vi, at cos 60 er lig med 1/2. Udfyld dette i formlen, og så kan vi løse: 10 Newton × 2 meter × 1/2 = 10 joule. 

Antag, baseret på ovenstående eksempel, at det tog 12 sekunder at flytte toget 5 meter. I så fald dividerer vi det udførte arbejde (86,6 joule) med tiden (12 sekunder) for at finde svaret. Så magten er: 86,6/12 = `7,22 watt. 
For eksempel kan vi i eksempelopgaven to trin tidligere antage, at toget i princippet havde en samlet mekanisk energi på 100 joule. Da kraften trækker toget i dette eksempel i bevægelsesretningen, er den positiv. Togets energi er TMEjeg + Wnc = 100 + 86,6 = 186 joule. Bemærk, at ikke-konservative kræfter er de kræfter, hvor den kraft, der kræves for at accelerere et objekt, afhænger af objektets vej. Friktion er et godt eksempel; en genstand, der skubbes en kort lige vej til et bestemt punkt, vil i gennemsnit opleve mindre friktion end en genstand, der skubbes en længere bugtende sti til samme endepunkt som den korte vej.
Beregn arbejdskraft
Indhold
I fysik betyder det "arbejdskraft" noget helt andet end daglig tale. For at være præcis, udtrykket "arbejdskraft" bruges når en fysisk kraft får en genstand til at bevæge sig. Generelt gælder det, at jo større forskydning en given kraft er, jo mere arbejde udføres der. Arbejdet kan beregnes med formlen Arbejde = F × D × cos(θ), hvor F = kraft (i newton), D = forskydning (i meter) og θ = vinklen mellem vektorkraften og bevægelsesretningen.
Trin
Del 1 af 3: Bestemmelse af arbejdskraft i en dimension

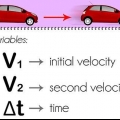
1. Bestem retningen af kraften og retningen af bevægelsen. Til at begynde med er det vigtigt at bestemme både retningen af kraften og objektets retning. Husk, at objekter ikke altid bevæger sig i samme retning som den kraft, der påføres dem; for eksempel, hvis du trækker en lille vogn i håndtaget, påfører du en diagonal kraft på den (hvis du er højere end vognen er høj) for at flytte den fremad. I dette afsnit behandler vi situationer, hvor kraft og bevægelse "godt" går i samme retning. For information om, hvordan man beregner arbejdskraft som denne "ikke" hvis ja, kan du læse mere nedenfor.
- For at gøre dette klart, vil vi løse følgende problem. Antag, at et legetøjstog trækkes af et lokomotiv. I dette tilfælde er både kraftvektoren og togets bevægelsesretning lig med hinanden; frem. I de næste par trin bruger vi denne information til at beregne arbejdet udført af lokomotivet.

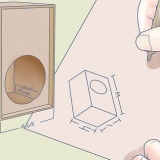
2. Bestem objektets forskydning. Den første variabel, vi skal bruge til formlen for arbejde, er D eller forskydning, som normalt er let at finde. Forskydning er den afstand et objekt flyttes i en lige linje. I videnskabelige problemer er denne information normalt givet, eller det er muligt at udlede det fra dataene. I den virkelige verden kan du finde forskydningen ved at måle afstanden mellem start- og slutpunktet (ikke langs den tilbagelagte sti, men "i luftlinje").

3. Bestem den kraft, der udøves på objektet. Bestem derefter størrelsen af den kraft, der bruges til at få objektet til at bevæge sig. Dette er et mål for "størrelse" af kraften; jo større kraft, jo større vil accelerationen af objektet være. Hvis størrelsen af kraften ikke er givet, kan du udlede den fra objektets masse og acceleration (forudsat at der ikke er andre kræfter at tage hensyn til) ifølge formlen F = M xA.

4. Multiplicer effekten gange afstanden. Hvis du kender størrelsen af kraften på objektet og afstanden det har bevæget sig, er resten let. Multiplicer disse to værdier sammen for at finde værket.

5. Giv svaret i joule. I fysik, o.-en. fødsel næsten altid udtrykt i joule. 1 Joule er defineret som 1 Newton udøvet på 1 meter, eller med andre ord, 1 Newton × meter. Dette virker logisk, fordi man multiplicerer en afstand med kraft og dermed udtrykker dette i Nm.
Del 2 af 3: At finde arbejde, når der påføres kraft fra en vinkel

1. Bestem kraften og forskydningen som normalt. Ovenfor diskuterede vi et problem om arbejde, hvor objektet og kraften går i samme retning. I virkeligheden er dette ofte ikke tilfældet. I de tilfælde, hvor kraften på og bevægelsen af objektet er modsat, skal du tage højde for forskellen mellem de to, og tage dette med i beregningen for det korrekte resultat. For at starte, find størrelsen af kraften og objektets forskydning som normalt.
- Lad os se på et andet eksempel. Lad os i dette tilfælde sige, at vi trækker toget ligesom i det foregående eksempel, men trækket er vinklet opad. Vi vil tage højde for dette i næste trin, men indtil videre holder vi os til det grundlæggende: togets forskydning og størrelsen af kraften på toget. Antag, at kraften har en størrelse på 10 newton og at forskydningen igen er lig med 2 meter, som før.

2. Bestem nu vinklen mellem kraftens retning og forskydningen. I modsætning til eksemplerne beskrevet ovenfor, er det nu nødvendigt at bestemme forskellen mellem de to retninger, udtrykt i vinklen. Hvis disse data ikke er givet, kan du måle dette eller udlede dette fra andre oplysninger, du har.

3. Multiplicer kraften F gange forskydningen D gange vinklen cos(θ). Når du kender forskydningen, kraften og vinklen (mellem vektor og bevægelse), er løsningen næsten lige så let, som den er uden at tage hensyn til vinklen. Bare tag cos for vinklen (du skal nok bruge en lommeregner til dette) og gange det med kraften og forskydningen for at finde dit svar (i joule).
Del 3 af 3: Brug en værdi for arbejdskraft

1. Du kan også invertere formlen for at finde afstanden, kraften eller vinklen. Formlen ovenfor er naturligvis nyttig ikke kun til at finde arbejde, men også, hvis det er givet arbejde, til at finde de andre variabler med samme formel. I disse tilfælde isolerer du blot den variabel, du ønsker at beregne og løse efter simple algebraiske principper.
- Antag at vide, at toget trækkes med en kraft på 20 Newton i en vinkel og bevæger sig langs sporet i en afstand på 5 meter og udfører 86,6 Joule arbejde. Men vi kender ikke den vinkel, hvor kraften virker på objektet. For at løse dette, lad os sætte variablen separat og regne den ud på denne måde:
- 86,6 = 20 × 5 × cos(θ)
- 86,6/100 = cos(θ)
- arccos(0,866) = θ = 30

2. Divider med den tid, det tog flytningen at finde evnen. Arbejdskraft er direkte relateret til "strøm". Magt er simpelthen en måde at udtrykke mængden af arbejde udført inden for et givet system over den tid, det har taget. Alt hvad du behøver at gøre for at finde kraften er det arbejde, der er udført for at flytte objektet, dividere med varigheden af flytningen. Effekt er udtrykt i enheder af Watt (lig med Joule per sekund).

3. Brug formlen TMEjeg + Wnc = TMEf at finde den mekaniske energi i et system. Arbejde kan også bruges til at bestemme energien i et givet system. I ovenstående formel, TMEjeg = er initial total mekanisk energi i systemet, TMEf = den endelig total mekanisk energi i systemet og Wnc = arbejdet udført på systemet på grund af ikke-konservative kræfter.. I denne formel, hvis kraften bevæger sig med forskydningsretningen, så er den positiv, og hvis den modsætter sig, er den negativ. Bemærk, at begge energivariabler kan findes med formlen (½)mv, hvor m = masse og v = volumen.
Tips
- Hvis det lykkes dig at løse et problem, så smil og klap dig selv på skulderen!
- Lav så mange øvelser som muligt, hvormed du lærer at forstå emnet.
- Fortsæt med at øve dig og prøv igen, hvis det ikke virker første gang.
- Lær følgende punkter om arbejdskraft:
- Arbejdskraft kan være positiv eller negativ. (Her mener vi den fysiske betydning af positiv og negativ, ikke den bogstavelige betydning.)
- Arbejdet er negativt, hvis kraften er modsat forskydningsretningen.
- Arbejdet er positivt, hvis kraften er lig med forskydningsretningen.
Artikler om emnet "Beregn arbejdskraft"
Оцените, пожалуйста статью
Populær