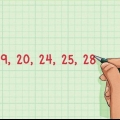
Lad os fortsætte med at arbejde med eksemplet ovenfor. Her er vores datasæt, der viser temperaturerne i grader Fahrenheit for forskellige genstande i et rum: {71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}. Hvis vi sorterer værdierne i sættet fra laveste til højeste, bliver dette vores nye sæt: {69, 69, 70, 70, 70, 70, 71, 71, 71, 72, 73, 300}. 
Bliv ikke forvirret af datasæt med et lige antal punkter - gennemsnittet af de to midterste punkter er ofte et tal, der ikke er i selve datasettet - det er okay. Men hvis de to midterpunkter er ens, vil gennemsnittet naturligvis også være dette tal - det er også dette okay. I vores eksempel har vi 12 point. De to midterste led er henholdsvis prikker 6 og 7 – 70 og 71. Så medianen af vores datasæt er middelværdien af disse to punkter: ((70 + 71) / 2)=70,5. 
I vores eksempel er seks point over medianen og seks under den. Så for at finde den første kvartil skal vi tage gennemsnittet af de to midterste punkter i de nederste seks punkter. Punkt 3 og 4 i de nederste seks er begge 70, så deres middelværdi er ((70 + 70) / 2)=70. Så vores værdi for Q1 er 70. 
Hvis vi fortsætter med ovenstående eksempel, ser vi, at de to midterste punkter af de seks punkter over medianen er 71 og 72. Middelværdien af disse to punkter er ((71 + 72) / 2)=71,5. Så vores værdi for Q3 er 71,5. 
I vores eksempel er værdierne for Q1 og Q3 henholdsvis 70 og 71,5 . For at finde interkvartilområdet beregner vi Q3 - Q1: 71,5 - 70=1,5. Dette virker, selvom Q1, Q3 eller begge tal er negative. For eksempel, hvis vores værdi for Q1 var -70, ville interkvartilområdet være 71,5 - (-70)=141,5, hvilket er korrekt. 
I vores eksempel er interkvartilområdet (71,5 - 70) eller 1,5. Gang dette med 1,5 og du får 2,25. Vi lægger dette tal til Q3 og trækker det fra Q1 for at finde de indre grænser som følger: 71,5 + 2,25=73,75 70 - 2,25=67,75 Så de indre grænser er 67,75 og 73,75. I vores datasæt er det kun ovntemperaturen - 300 grader Fahrenheit - der er uden for dette område. Så dette kan være en mild outlier. Men vi mangler også endnu at afgøre, om denne temperatur er en ekstrem afviger, så lad os ikke hoppe til konklusioner endnu.

I vores eksempel gange vi interkvartilområdet med 3, og vi kommer frem til (1,5 *3) eller 4,5. Vi kan nu finde de ydre grænser på samme måde som de indre grænser: 71,5 + 4,5=76 70 - 4,5=65,5 Så de ydre grænser er 65,5 og 76. Datapunkter, der er uden for de ydre grænser, betragtes som ekstreme outliers. I vores eksempel er ovntemperaturen, 300 grader Fahrenheit, et godt stykke uden for de ydre grænser. Så ovntemperaturen er sikker en ekstrem afviger.

Et andet kriterium, der skal overvejes, er, om outliers påvirker gennemsnittet af et datasæt på en måde, der er skæv eller vildledende. Dette er især vigtigt, hvis du har til hensigt at drage konklusioner ud fra gennemsnittet af dit datasæt. Lad os gennemgå vores eksempel. Siden den højt Selvom det er usandsynligt, at ovnen nåede en temperatur på 300°F på grund af en eller anden uforudset naturkraft, kan vi i vores eksempel konkludere med næsten 100 % sikkerhed, at ovnen blev efterladt tændt ved et uheld, hvilket resulterede i en unormal høj temperaturaflæsning. Derudover, hvis vi ikke fjerner udliggeren, er vores datasæt gennemsnittet ud til (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73 + 300)/12=89,67 °F, mens gennemsnittet uden outlieren kommer ud ved (69 + 69 + 70 + 70 + 70 + 70 + 71 + 71 + 71 + 72 + 73)/11=70,55 °F. Da outlieren var forårsaget af menneskelige fejl, og da det er forkert at sige, at den gennemsnitlige rumtemperatur var tæt på 32°C, må vi vælge at vælge vores outlier fjerne. 
Forestil dig for eksempel, at vi designer et nyt lægemiddel for at få fisk til at vokse sig større i en dambrug. Lad os bruge vores gamle datasæt ({71, 70, 73, 70, 70, 69, 70, 72, 71, 300, 71, 69}), bortset fra at hvert punkt nu repræsenterer massen af en fisk (i gram) efter behandling med et andet eksperimentelt lægemiddel fra fødslen. Med andre ord gav det første lægemiddel en fisk en masse på 71 gram, det andet gav en anden fisk en masse på 70 gram, og så videre. I denne situation 300. er stadig en kæmpe outlier, men vi skal ikke fjerne den nu. Fordi, hvis vi antager, at outlieren ikke er resultatet af en fejl, repræsenterer den en stor succes i vores eksperiment. Lægemidlet, der producerede en 300 grams fisk, virkede bedre end noget andet lægemiddel, så dette er det mest vigtigt datapunkt i vores sæt, snarere end mindst vigtigt datapunkt.
Beregn outliers
Indhold
EN afvigende eller afvigende i statistik, et datapunkt, der adskiller sig væsentligt fra de andre datapunkter i en stikprøve. Ofte påpeger outliers over for statistikere anomalier eller fejl i målingerne, hvorefter de kan fjerne outlieren fra datasættet. Hvis de faktisk vælger at fjerne outliers fra datasættet, kan det medføre væsentlige ændringer i konklusionerne fra undersøgelsen. Derfor er det vigtigt at beregne og bestemme outliers, hvis man ønsker at fortolke statistiske data korrekt.
Trin

1. Lær, hvordan du spotter potentielle outliers. Før vi kan beslutte, om vi skal fjerne unormale værdier fra et bestemt datasæt, skal vi selvfølgelig genkende de mulige outliers i datasættet. Generelt er outliers de datapunkter, der afviger væsentligt fra tendensen, at de andre værdier i den indstillede form – med andre ord, de skyde ud af de andre værdier. Det er normalt let at genkende dette i tabeller og (især) i grafer. Hvis datasættet tegnes visuelt, vil outlierne være `langt væk` fra de andre værdier. For eksempel, hvis de fleste punkter i et datasæt danner en lige linje, vil outliers ikke være i overensstemmelse med denne linje.
- Lad os se på et datasæt, der viser temperaturerne på 12 forskellige genstande i et rum. Hvis temperaturen på 11 af genstandene svinger omkring 21°C med højst et par grader, mens en genstand, en ovn, har en temperatur på 150°C, kan man med et øjeblik se, at ovnen formentlig er en yderside.

2. Sorter alle datapunkter fra lav til høj. Det første trin i beregningen af outliers er at finde medianværdien (eller den midterste værdi) af datasættet. Denne opgave bliver meget lettere, hvis værdierne i sættet er i rækkefølge fra laveste til højeste. Så før du fortsætter, skal du sortere værdierne i dit datasæt på denne måde.

3. Beregn medianen af datasættet. Medianen af et datasæt er det datapunkt, hvor halvdelen af dataene er over det, og halvdelen af dataene er under - det er dybest set "centeret" af datasættet. Hvis datasættet indeholder et ulige antal punkter, er medianen let at finde – medianen er punktet med lige så mange punkter over som under det. Hvis der er et lige antal point, da der ikke er ét midtpunkt, skal du tage gennemsnittet af de to midtpunkter for at finde medianen. Ved beregning af outliers er medianen normalt angivet med variablen Q2 - fordi den ligger mellem Q1 og Q3, den første og tredje kvartil. Vi vil bestemme disse variabler senere.

4. Beregn den første kvartil. Dette punkt, som vi omtaler som variablen Q1, er det datapunkt, under hvilket 25 procent (eller en fjerdedel) af observationerne ligger. Med andre ord er dette midtpunktet af alle punkter i dit datasæt under medianen. Hvis der er et lige antal værdier under medianen, skal du igen gennemsnittet de to midterste værdier for at finde Q1, som du måske allerede har gjort for at bestemme medianen selv.

5. Beregn den tredje kvartil. Dette punkt, som vi betegner med variablen Q3, er det datapunkt, over hvilket 25 procent af dataene ligger. At finde Q3 er praktisk talt det samme som at finde Q1, undtagen i dette tilfælde ser vi på punkterne over medianen.

6. Find interkvartilområdet. Nu hvor vi har bestemt Q1 og Q3, skal vi beregne afstanden mellem disse to variable. Afstanden mellem Q1 og Q3 kan findes ved at trække Q1 fra Q3. Den værdi, du får for interkvartilområdet, er afgørende for at bestemme grænserne for ikke-afvigende punkter i dit datasæt.

7. Find de `indre grænser` for datasættet. Du kan identificere outliers ved at bestemme, om de falder inden for en række numeriske grænser; de såkaldte `indre grænseværdier` og `ydre grænseværdier`. Et punkt, der falder uden for datasættets indre grænser, klassificeres som en mild udligger, og et punkt, der falder uden for de ydre grænser, er klassificeret som en ekstrem udligger. For at finde de indre grænser for dit datasæt skal du først gange interkvartilområdet med 1,5. Tilføj resultatet til Q3 og træk det fra Q1. De to resultater er de indre grænser for dit datasæt.


8. Find datasættets `ydre grænser`. Det gør du på samme måde som med de indre grænser, med den eneste forskel, at du multiplicerer interkvartilområdet med 3 i stedet for med 1,5. Du tilføjer derefter resultatet til Q3 og trækker fra Q1 for at finde de ydre grænser.


9. Brug en kvalitativ vurdering til at afgøre, om du skal "kassere" afvigelserne. Med ovenstående metode kan du bestemme, om visse punkter er milde outliers, ekstreme outliers eller ingen outliers overhovedet. Men tag ikke fejl – at anerkende et punkt som en afviger gør det kun til et kandidat skal fjernes fra datasættet, og ikke straks fjernes en prik skal blive til. Det red hvorfor en outlier er forskellig fra resten af punkterne i sættet er afgørende for, om outlieren skal fjernes. Generelt fjernes outliers forårsaget af en fejl - f.eks. en fejl i målingerne, i optagelserne eller i det eksperimentelle design -. I modsætning hertil er outliers, der ikke er forårsaget af fejl, og som afslører ny, uforudset information eller tendenser, normalt ikke slettet.

10. Forstå vigtigheden af (nogle gange) at fastholde outliers. Mens nogle outliers bør fjernes fra et datasæt, fordi de er resultatet af fejl, eller fordi de vildledende skævvrider resultaterne, bør andre outliers bevares. For eksempel, hvis en outlier er opnået korrekt (dvs. ikke resultatet af en fejl), og/eller hvis outlieren giver en ny indsigt i det fænomen, der skal måles, bør den ikke fjernes med det samme. Videnskabelige eksperimenter er særligt følsomme situationer, når det kommer til at håndtere outliers - fejlagtig fjernelse af en outlier kan betyde, at man kasserer vigtig information om en ny trend eller opdagelse.
Tips
- Hvis du finder outliers, så prøv at forklare dem, før du fjerner dem fra datasættet; de kan indikere målefejl eller afvigelser i fordelingen.
Fornødenheder
- Lommeregner
Artikler om emnet "Beregn outliers"
Оцените, пожалуйста статью
Populær