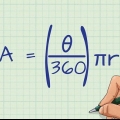Sådan beregnes lotteri odds

Indhold

Trin
Tips
Advarsler

Alle har hørt sammenligninger om oddsene for at vinde i lotteriet versus oddsene for andre usandsynlige begivenheder, såsom at blive ramt af lynet. Det er sandt, oddsene for at vinde jackpotten på et spil som Powerball eller ethvert andet pick-6 lotteri er utroligt lave. Men hvor lavt? Og hvor ofte skal du spille for at øge din chance? Disse svar kan findes nøjagtigt med nogle simple beregninger.

Trin

Metode 1 af 3: Beregning af Jackpot-odds

1. Forstå de anvendte beregninger. Oddsene for at vinde et lotteri, hvor tal er valgt fra en rækkefølge, uanset rækkefølge, er defineret af formlen

n! r! (n - r)!

${frac{n!}{r!(n-r)!}}$ . I denne formel repræsenterer n det samlede antal mulige tal, og r repræsenterer antallet af tal, der vil blive valgt. det `!` står for factorial, hvor for hvert heltal n er n*(n-1)*(n-2)... etc., indtil 0 er nået. For eksempel: 3! betyder da

3 \times 2 \times 1

$3 gange 2 gange 1$ .

Et simpelt eksempel: forestil dig, at du skal vælge mellem to tal og tallene 1 til 5. Din sandsynlighed for at vælge de to `korrekte` tal (vindertallene) vil så blive defineret som $5! 2! \times 3!$ ${frac{5!}{2!gange 3!}}$ .
Dette er så løst som $5 \times 4 \times 3 \times 2 \times 1 2 \times 1 \times 3 \times 2 \times 1$ ${frac{5 gange 4 gange 3 gange 2 gange 1}{2 gange 1 gange 3 gange 2 gange 1}}$ , enten $120 \div 12$ $120div 12$ , og det er 10.
Så din chance for at vinde dette spil er 1 ud af 10.
Beregning af faktoren kan blive forvirrende, især når det kommer til større tal. De fleste lommeregnere har en faktoriel funktion for at gøre disse beregninger lidt nemmere. Alternativt kan du også komme ind på fakultetet i Duck Duck Go-søgemaskinerne (som f.eks. `55!`) eller Google for at få svaret.

Billede med titlen Beregn Lotto-odds Trin 2

2. Bestem lotterireglerne. Størstedelen af pengemillioner, Powerball og andre store lotterier, bruger nogenlunde de samme regler. Fem eller seks tal vælges fra en stor pulje af tal i tilfældig rækkefølge. Tal kan ikke gentages. I nogle spil tilføjes et fast tal til sidst (Powerball i Powerball-spillene er et eksempel). Powerballs standardregler viser, at fem tal (ikke inklusive Powerball) er valgt blandt 69 mulige tal.

Andre spil kræver muligvis, at du vælger mellem fem eller seks numre eller mere fra en større eller mindre pulje af numre.

Billede med titlen Beregn Lotto-odds Trin 3

3. Anvend tallene på ligningen for sandsynligheden. Den første del af Powerball-sandsynligheden beregnes som sandsynligheden for at vælge de første fem tal korrekt. Dette beregnes bekvemt med den tidligere indførte sandsynlighedsformel. Så ligningen for disse særlige linjer bliver:

69! 5! (69 - 5)!

${frac{69!}{5!(69-5)!}}$ , at forenkle til

69! 5! \times 64!

${frac{69!}{5!gange 64!}}$ .

Billede med titlen Beregn Lotto-odds Trin 4

4. Beregn din chance for at vælge det rigtige tal. Løsning af ligningen gøres bedst med en søgemaskine eller lommeregner, da de anvendte tal er besværlige at skrive ned mellem trinene. Når den er løst, vil ligningen være tallet 11.238.giv 513. Det betyder, at du har en chance på 1 til 11.238.513 for at vælge de fem numre korrekt.

Billede med titlen Beregn Lotto-odds Trin 5

5. Multiplicer for at få det endelige tal. For at tage højde for sandsynligheden for at vælge Powerball korrekt og vinde jackpotten, skal du blot gange tallet fra det forrige resultat med størrelsen af Powerball-puljen. Til standardspillet er der 26 mulige Powerball-numre. Så du multiplicerer det forrige resultat (11.238.513 i dette tilfælde) med det endelige tal (som er 26), for at beregne din endelige sandsynlighed (som er 292.201.338).

Så din chance for at vælge de første fem numre korrekt og Powerball er 1 ud af 292.201.338.

Metode 2 af 3: Bestemmelse af sandsynligheden for mindre præmier

Billede med titlen Beregn Lotto-odds Trin 6

1. Start med jackpot-chancen. I de fleste tilfælde er der mindre præmier tilgængelige, som kræver, at du vælger nogle af tallene korrekt. Ved at vælge tre eller fire af de vindende numre kan du vinde et beløb på hundredtusindvis af euro. I dette tilfælde er dine sandsynligheder baseret på at beregne sandsynligheden for at vælge et par rigtige tal, kombineret med et modsat antal forkerte tal. Dette kræver, at du først kender det samlede antal mulige kombinationer. Disse kan beskrives med sandsynligheden for at vælge alle vindende tal korrekt.

Du skal først have beregnet jackpot-odds som beskrevet i metoden `Beregning af jackpot-odds`.
For at forenkle beregningerne bruger vi sandsynligheden for korrekt valg af de første fem Powerball-tal. I den anden metode beregnede vi, at dette er 1 ud af 11.238.513 er.

Billede med titlen Beregn Lotto-odds Trin 7

2. Skriv ligningen. Din chance for at vinde `k` fra antallet af `r`-tal fra den samlede pulje af tal `n` kan defineres som:

r! k! (r - k)! \times (n - r)! (r - k)! (n - r - k)! \frac{n!}{r! (n - r)!}

${frac{{frac{r!}{k!(rk)!}}gange {frac{(nej)!}{(rk)!(nrk)!}}}{{frac{n! }{r!(nr)!}}}}$ . Denne formel virker meget mere kompliceret, men i virkeligheden er den ikke mere end tre kopier af den simple sandsynlighedsligning fra den anden metode. Indtast blot dine tal for n, r og k.

For eksempel er din chance for at vinde tre ud af fem tal fra en pulje på 69 derefter beskrevet af ligningen

5! 3! \times 2! \times 64! 2! \times 61! \frac{69!}{5! \times 64!}

${frac{{frac{5!}{3!gange 2!}}gange {frac{64!}{2!gange 61!}}}{{frac{69!}{5! times 64!}}}}$ .

Billede med titlen Beregn Lotto-odds Trin 8

3. Bestem din chance for at vinde. Ligesom med grundligningen løses denne ligning bedst ved at indtaste det hele i en lommeregner eller søgemaskine, da nogle af regnestykkets mellemtal er for store til at skrive på. Hvis det løses rigtigt, vil resultatet være sandsynligheden for, at tre af de fem Powerball-numre er valgt korrekt.

I eksemplet bliver dette 579,76. Så din chance for at vælge tre ud af fem korrekt er 1 ud af 579,76.

Billede med titlen Beregn Lotto-odds Trin 9

4. Vælg det ønskede antal vindernumre. Du kan justere din beregning ved at ændre værdien af k for at bestemme sandsynligheden for at vinde forskellige sekvenser af de fem tal. Din chance for at vinde vil falde, efterhånden som k bliver større og omvendt.

Metode 3 af 3: Beregning af andre lotto-odds

Billede med titlen Beregn Lotto-odds Trin 10

1. Bestem den forventede værdi af en lottokupon. Den forventede værdi af en lottokupon repræsenterer den teoretiske gevinst på en kupon. Det er med andre ord det beløb, du teoretisk set kunne få tilbage efter at have købt en lottokupon. Det kan beregnes ved at gange oddsene for en given udbetaling (jackpot, 4 korrekte tal, 3 rigtige tal osv.) med udbetalingsbeløbet, og læg dem derefter sammen. Dette tal er dog tydeligt forvrænget af den enorme jackpot.

Normalt vil din udbetaling være meget mindre end den forventede værdi.
Ved standard 5+1 af 69 og 26 Powerball er den forventede værdi af en billet cirka $1,78.

Billede med titlen Beregn Lotto-odds Trin 11

2. Sammenlign prisen med den forventede værdi. Du kan bestemme de forventede fordele ved at spille i lotteriet ved at sammenligne den forventede værdi af en billet med prisen på en billet. Normalt vil det være meget mindre. Derudover afviger dit faktiske overskud meget fra den forventede værdi, på trods af navnet. De fleste mennesker får kun en brøkdel af den ideelle forventede værdi, hvis de overhovedet får noget.

Nogle lotterier betaler dog mere end andre.

For eksempel, på et tidspunkt havde $1-lotterisedlen fra New York Take Five-lotteriet en forventet værdi svarende til prisen. Dette betød, at ved at spille dette lotteri, kunne spillerne forvente ikke at tabe.

Billede med titlen Beregn Lotto-odds Trin 12

3. Bestem stigningen i chance ved at spille flere gange. At spille i lotteriet flere gange kan øge din gennemsnitlige chance for at vinde, uanset hvor lidt. Det er lettere at forestille sig denne stigning som et fald i din chance for at tabe. For eksempel, hvis din gennemsnitlige chance for at vinde er 1 ud af 250.000.000, så er din sandsynlighed for at tabe uafgjort

249.999.999 \div 250.000.000

$249.999.999div 250.000.000$ , og det svarer til et tal meget tæt på 1 (0,99999...). Hvis du spiller to gange, er tallet i kvadrat (

(249.999.999 \div 250.000.000) 2

$(249.999.999div 250.000.000)^{{2}}$ ), hvilket skaber et lidt lavere tal end 1 (og derfor en større chance for at vinde).

Billede med titlen Beregn Lotto-odds Trin 13

4. Find det antal gange du skal spille for at have en god chance for at vinde. De fleste lotterispillere er overbevist om, at hvis de spiller ofte nok, kan de øge deres odds for at vinde markant. Det er rigtigt, at ved at spille oftere, har du større chance for at vinde. Denne stigning er dog ikke signifikant længe. For eksempel, givet ovenstående odds (1 ud af 250 millioner pr. spil), skal du spille cirka 180 millioner gange for at have en 50-50 chance for at vinde.

Med andre ord: hvis du køber ti lottokuponer om dagen, har du 50 procent chance for at vinde, hvis du køber denne 49.300 år fortsæt.

Det betyder dog ikke, at køb af to billetter på den dag garanterer en gevinst. Din samlede chance for at vinde forbliver omkring 50 procent.

Tips

Fald ikke for lotteri-svindel, hvor nogen hævder at have en garanteret måde at vinde på. Hvis nogen havde en garanteret måde at vinde på, ville de virkelig ikke stoppe sig selv ved at fortælle dig det.
Ethvert sæt tal har nøjagtig de samme sandsynligheder som ethvert andet sæt. 32-45-22-19-09-11 er derfor lige så sandsynligt som 1-2-3-4-5-6.

Advarsler

Hvis du tror, du har et spilleproblem, har du det sandsynligvis. Gamblers Anonymous er en god kilde til information og hjælp til mennesker, der beskæftiger sig med ludomani.
Spil ikke mere, end du har råd til at tabe.

Artikler om emnet "Beregn lotteri odds"

Beregn joule

Beregn procenter

Beregn rabatten på et produkt

Beregn arealet af et segment

Оцените, пожалуйста статью