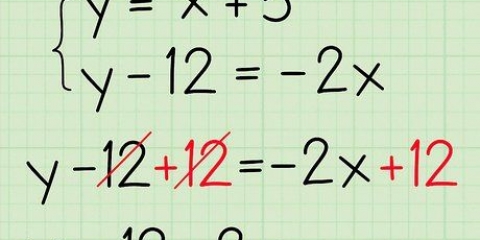Beregning af sandsynlighed: 10 trin (med billeder)

Indhold

Trin

Sandsynlighed er graden af sandsynlighed for, at en bestemt begivenhed vil indtræffe for en række mulige udfald. Sandsynlighed giver dig mulighed for at nærme dig et problem med logik, selvom der er en vis grad af usikkerhed. Lær, hvordan du bruger almindelige matematiske færdigheder til at beregne sandsynligheder her.

Trin

Del 1 af 4: Sandsynlighed for en enkelt tilfældig hændelse

1. Bestem begivenheden og mulige udfald. Sandsynlighed er sandsynligheden for, at en bestemt begivenhed vil indtræffe divideret med antallet af mulige udfald. Så lad os sige, at du vil beregne sandsynligheden for at kaste en treer med en almindelig terning. "smid en treer" er begivenheden, og da vi ved, at en almindelig terning med 6 sider har lige stor chance for at lande på hver side, er antallet af udfald 6. Her er to andre eksempler for at komme i gang:

Eksempel 1: Hvad er sandsynligheden for, at du vælger en dag, der falder på en weekend, hvis du vælger en hvilken som helst dag i ugen??

"At vælge en dag, der falder på weekenden" er vores begivenhed, og antallet af udfald er det samlede antal dage i ugen.

Eksempel 2: En flaske indeholder 4 blå kugler, 5 røde kugler og 11 hvide kugler. Hvis en kugle er tilfældigt plukket fra flasken, hvad er sandsynligheden for, at den er rød??

"At vælge en rød marmor" er vores begivenhed, og antallet af udfald er det samlede antal kugler i flasken, 20.

Billede med titlen Beregn sandsynlighed Trin 2

2. Divider antallet af hændelser med antallet af mulige udfald. Dette giver os sandsynligheden for, at en enkelt begivenhed indtræffer. I tilfælde af at kaste en tre med en terning, er antallet af begivenheder 1 (der er kun en 3 på en almindelig terning), og antallet af udfald er seks. Du kan også se dette som: 1 ÷ 6, 1/6, .166 eller 16.6 %. Sådan finder du oddsene for resten af eksemplet:

Eksempel 1: Hvad er sandsynligheden for at vælge en dag, der falder på en weekend, hvis en tilfældig ugedag er valgt?

Antallet af begivenheder er to (fordi to dage i ugen falder i weekenden), og antallet af udfald er syv. Sandsynligheden er 2 ÷ 7=2/7 eller .285 eller 28.5 %.

Eksempel 2: En flaske indeholder 4 blå kugler, 5 røde kugler og 11 hvide kugler. Hvis en marmor er tilfældigt plukket fra flasken, hvad er sandsynligheden for, at denne marmor er rød??

Antallet af begivenheder er fem (fordi der er fem kugler i alt), og antallet af udfald er 20. Sandsynligheden er 5 ÷ 20=1/4 eller 0,25 eller 25 %.

Del 2 af 4: Beregning af sandsynligheden for flere tilfældige hændelser

1. Bryd problemet i håndterbare stykker. At beregne sandsynligheden for flere hændelser er ensbetydende med at opdele problemet i "separate sandsynligheder". Her er tre eksempler:

Billede med titlen Beregn sandsynlighed Trin 3

Eksempel 1:Hvad er sandsynligheden for at slå to gange fem med en almindelig sekssidet terning??

Du ved, at sandsynligheden for at kaste en femmer er 1/6, og sandsynligheden for at kaste endnu fem med den samme terning er også 1/6.
Det er `uafhængige begivenheder`, fordi det, du kaster første gang, ikke har nogen indflydelse på resultatet af det andet kast; det er muligt, at du slår en 3`er og en anden treer.

Eksempel 2:To kort trækkes tilfældigt fra et sæt kort. Hvad er sandsynligheden for, at begge kort er kløver??

Sandsynligheden for at det første kort er en kølle er 13/52 eller 1/4 (Der er 13 køller i hver kulør). Nu ved vi, at sandsynligheden er 12/51 for, at det andet kort er en kløver.

Du bestemmer chancen for afhængige begivenheder. Det er fordi, hvad du gør første gang, påvirker den anden; Hvis du trækker en 3-kølle og ikke sætter den tilbage, er der et kort og også en kølle mindre i farven (51 i stedet for 52).

Eksempel 3: En flaske indeholder 4 blå kugler, 5 røde kugler og 11 hvide kugler. Hvis tre kugler tilfældigt plukkes fra flasken, hvad er sandsynligheden for, at den første kugle er rød, den anden kugle er blå og den tredje er hvid?

Sandsynligheden for, at den første marmor er rød, er 5/20 eller 1/4. Sandsynligheden for, at den anden marmor er blå er 4/19, fordi der er en marmor mindre, men ikke færre blå kugler. Og sandsynligheden for at den tredje kugle er hvid er 11/18, fordi vi valgte to kugler før. Dette er en anden bestemmelse i en selvstændig begivenhed.

Billede med titlen Beregn sandsynlighed Trin 4

2. Multiplicer sandsynligheden for hver begivenhed. Resultatet giver sandsynligheden for, at flere hændelser indtræffer efter hinanden. Her er, hvad du kan gøre:

Eksempel 1:Hvad er sandsynligheden for at kaste to gange en femmer med en almindelig terning?? Sandsynligheden for begge uafhængige hændelser er 1/6.

Dette giver os: 1/6 x 1/6=1/36 eller 0,027 eller 2,7 %.

Eksempel 2: To kort trækkes tilfældigt fra et sæt kort. Hvad er sandsynligheden for, at begge kort er kløver??

Sandsynligheden for den første hændelse er 13/52. Sandsynligheden for den anden hændelse er 12/51. Sandsynligheden er 13/52 x 12/51=12/204 eller 1/17 eller 5,8 %.

Eksempel 3: En flaske indeholder 4 blå kugler, 5 røde kugler og 11 hvide kugler. Hvis tre kugler er tilfældigt plukket fra en flaske, hvad er sandsynligheden for, at den første kugle er rød, den anden kugle er blå og den tredje er hvid?

Sandsynligheden for den første hændelse er 5/20. Sandsynligheden for den anden hændelse er 4/19. Og sandsynligheden for den tredje begivenhed er 11/18. Sandsynligheden er 5/20 x 4/19 x 11/18=44/1368 eller 3,2 %.

Del 3 af 4: Konvertering af odds til tilfældigheder

Billede med titlen Beregn sandsynlighed Trin 5

1. Bestem, hvad oddsene er (oddsforholdet). For eksempel er en golfspiller favorit til at vinde med en chance på 9/4. Oddsene for en begivenhed er forholdet mellem sandsynligheden for, at noget vil ske, og sandsynligheden for, at det ikke vil ske.

I eksemplet med forholdet 9:4 repræsenterer 9 sandsynligheden for, at golfspilleren vinder. 4 repræsenterer sandsynligheden for, at dette ikke vil ske. Så dette forhold viser, at golfspilleren er mere tilbøjelig til at vinde end at tabe.
Husk, at ved væddemål i sport og af bookmakere, er odds udtrykt som "odds imod," hvilket betyder, at sandsynligheden for, at en begivenhed ikke indtræffer, nedskrives først, og sandsynligheden for, at en begivenhed indtræffer efterfølgende. Selvom dette kan være forvirrende, er det godt at være opmærksom på dette. I denne artikel vil vi ikke komme nærmere ind på "odds imod".

Billede med titlen Beregn sandsynlighed Trin 6

2. Konverter odds til tilfældigheder. Konvertering af odds er ret nemt. Opdel oddsene i to separate begivenheder, der lægger op til at give oddsene.

Begivenheden, som golfspilleren vil vinde, er 9; den begivenhed, som golfspilleren vil tabe, er 4. summen af fordele og ulemper er 9 + 4 eller 13.

Beregningen er nu den samme som at beregne sandsynligheden for en enkelt hændelse.

9 13=0,692 eller 69,2 %. Så sandsynligheden for at golfspilleren vinder er: 9/13.

Del 4 af 4: Sandsynlighedsreglerne

Billede med titlen Beregn sandsynlighed Trin 7

1. Sørg for, at to begivenheder eller resultater udelukker hinanden. Det betyder, at de ikke begge kan handle på samme tid.

Billede med titlen Beregn sandsynlighed Trin 8

2. Tilfældighed kan ikke være negativ. Hvis dine beregninger viser et negativt tal, så tjek hvad du har gjort.

Billede med titlen Beregn sandsynlighed Trin 9

3. Sandsynligheden for alle mulige hændelser skal være 1 ud af 100 %. Hvis sandsynligheden for alle mulige hændelser ikke opfylder dette, har du lavet en fejl et sted, fordi du har forsømt en eventuel hændelse.

Sandsynligheden for at slå en treer med en almindelig terning er 1/6. Dette gælder naturligvis også for de øvrige tal, og heraf følger: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6=6/6 eller 1 eller 100 %.