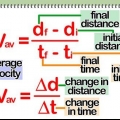
-enav = /t (Symbolet Δ eller "delta" betyder bare "lave om.") -enav = /(tf - tjeg) I denne ligning er vf terminalhastigheden og vjeg er starthastigheden. 
Fra nu af vil vi bruge positive tal til at beskrive bevægelsen til højre, så vi ikke behøver at angive retningen hver gang. Hvis bilen starter forlæns og slutter baglæns, skal du sørge for at skrive den sidste hastighed som et negativt tal. 
Sørg for, at hastighed og tid altid er skrevet i de samme enheder. For eksempel, hvis din hastighed er registreret i km/t, så skal tiden også registreres i timer. 
-enav = /(10s - 0s) -enav = /(10s) -enav = 50 m/s/s Dette kan også noteres som 50 m/s. 
Bilen kunne starte ved 0 m/s og accelerere kontinuerligt i 10 sekunder, indtil den når 500 m/s. Bilen kunne starte ved 0 m/s, accelerere hurtigt til 900 m/s og derefter decelerere til 500 m/s fra tiende sekund. Bilen kunne starte ved 0 m/s, stå stille i 9 sekunder og accelerere meget hurtigt til 500 m/s fra tiende sekund. 

vende - vkom igang = + eller - ? 
Det blå tog bevæger sig hurtigere langs den positive side af linjen og accelererer dermed fra +5 m/s til +7 m/s. Sluthastigheden minus starthastigheden er 7 - 5 = +2. Da ændringen i hastigheden er positiv, er accelerationen det også. Det røde tog kører hurtigere langs den negative side og starter dermed med -5 m/s men slutter med -7 m/s. Sluthastigheden minus starthastigheden er -7 - (-5) = -7 + 5 = -2 m/s. Da ændringen i hastigheden er negativ, er accelerationen det også. 
Men hvis en helikopter flyver med en hastighed på -100 km i timen og accelererer med -50 km i timen, så er der positiv acceleration. Dette skyldes, at hastighedsændringen var positiv: -50 - (-100) = +50, selvom hastighedsændringen ikke var nok til at vende helikopterens retning.
Beregn gennemsnitsacceleration
Indhold
Acceleration er en størrelse, der beskriver en ændring i hastighed, og inkluderer både en ændring i hastighed og en ændring i retning. Du skal bruge den gennemsnitlige acceleration for at bestemme objektets gennemsnitshastighed over en given tid. Da det ikke er noget, de fleste regner med i det daglige, kan accelerationsproblemer føles lidt mærkelige, men med den rigtige tilgang forstår du dem fuldstændigt på kort tid.
Trin
Del 1 af 2: Beregning af den gennemsnitlige acceleration

1. Forstå hvad acceleration er. Acceleration beskriver hvor hurtigt noget går hurtigere eller bremser. Konceptet er så enkelt, som det lyder, selvom din lærebog måske beskriver det som "ændringen af hastigheden pr. tidsenhed." Accelerationen kan også beskrive den retning, et objekt bevæger sig i, som du kan inkludere som en beskrivelse eller som en del af formlen:
- Normalt, hvis et objekt flyttes til `højre`,op ellerfrem træk, noteres disse som et positivt (+) tal.
- Hvis et objekt til venstre, ned, eller tilbage bevægelser, brug et negativt (-) tal til accelerationen.

2. Definitionen som en formel. Som nævnt ovenfor er acceleration ændringen af hastigheden pr. tidsenhed. Der er to måder at skrive dette på som en formel:

3. Bestem objektets begyndelses- og sluthastighed. For eksempel, hvis en bil accelererer fra stilstand til 500 meter/sekund til højre, vil starthastigheden være 0 m/s, og sluthastigheden vil være 500 m/s til højre.

4. Bemærk ændringen over tid. For eksempel kan bilen bruge 10 sekunder for at nå terminalhastigheden. Medmindre andet er anmodet om i erklæringen, betyder dette normalt tf = 10 sekunder og tjeg = 0 sekunder.

5. Brug disse tal til at beregne den gennemsnitlige acceleration. Indsæt hastigheden og tiden i formlen for at finde den gennemsnitlige acceleration. I vores eksempel:

6. Forstå resultatet. Den gennemsnitlige acceleration beskriver, hvor hurtigt hastigheden i gennemsnit ændrer sig i løbet af den tid, vi ønsker at undersøge. Ovenstående eksempel accelererede bilen til venstre, og hastigheden steg med 50 m/s hvert sekund. Bemærk, at de nøjagtige bevægelsesdata kan ændre sig, så længe bilen ender med den samme totale ændring i hastighed og tid:
Del 2 af 2: Forståelse af positiv og negativ acceleration

1. Hvad den positive og negative hastighed repræsenterer.Selvom vektorhastigheden altid angiver en bestemt retning, kan det blive irriterende at blive ved med at gentage "op" eller "nord" eller "mod væggen" at skulle skrive. I stedet antager de fleste problemer, at objektet bevæger sig langs en lige linje. Normalt angives en bevægelse til højre som positiv (+) og en bevægelse til venstre som negativ hastighed (-).
- Et eksempel: et blåt tog kører mod øst med en hastighed på 500 m/s. Et rødt tog kører vestpå med samme hastighed, men da det er i den modsatte retning, skriver vi det som -500 m/s.

2. Brug definitionen af acceleration til at bestemme + eller – tegn. Acceleration er ændringen i hastighed i forhold til tid. Hvis du ikke er sikker på, om accelerationen er negativ eller positiv, kan du se, hvad hastighedsændringen er, og hvad du kan udlede:

3. Acceleration forklaret i begge retninger. Antag, at et blåt tog og et rødt tog kører væk fra hinanden med en hastighed på 5 m/s. Vi kan forestille os dette på en tallinje, hvor det blå tog bevæger sig med en hastighed på +5 m/s langs den positive side af linjen, og det røde tog bevæger sig langs den negative side med en hastighed på -5 m/s. Hvis hvert tog begynder at accelerere, indtil det når en hastighed 2 m/s hurtigere i bevægelsesretningen, har toget en positiv eller negativ acceleration? Lad os se:

4. Forståelse af forsinkelse. Antag, at et fly har en starthastighed på 500 km i timen og derefter sænker farten til 400 km i timen. Mens det altid bevæger sig i en positiv, fremadrettet retning acceleration af flyet negativ, fordi det "langsommere frem" så flyt for det. Du kan kontrollere dette på samme måde som i ovenstående eksempler: 400 - 500 = -100, så accelerationen er negativ.
Tips
- Acceleration og hastighed er begge dele vektorer, hvilket betyder, at de også angiver retningen af bevægelsen. Mængder, der ikke giver information om retning, kaldes skalarer. Hastighed, længde og antallet af æbler i en kurv er alle skalarer.
Artikler om emnet "Beregn gennemsnitsacceleration"
Оцените, пожалуйста статью
Populær