Beregning af arealet af en ellipse: 5 trin (med billeder)

Indhold

Trin
- Del 1 af 2: Beregning af arealet
- Del 2 af 2: Forstå hvorfor det virker
Tips

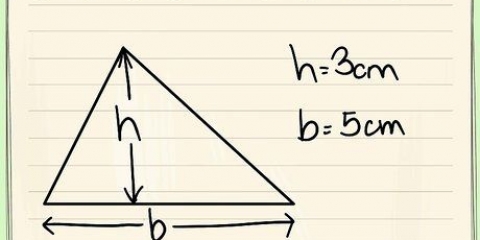
En ellipse er en todimensionel form, som du måske allerede kender fra geometriklassen, som ligner en aflang cirkel. At beregne arealet af en ellipse er let, når du kender længden af den største radius og den mindste radius.

Trin

Del 1 af 2: Beregning af arealet

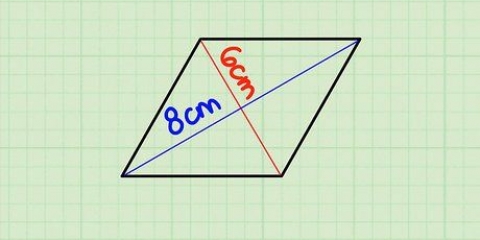
1. Find den største radius af ellipsen. Dette er afstanden fra midten af ellipsen til den yderste kant af ellipsen. Betragt dette som radius af den `tykke` del af ellipsen. Mål dette, eller søg efter den passende etiket i diagrammet. Vi kalder denne værdi -en.

Du kan også kalde dette `hovedaksen`.

Billede med titlen Beregn arealet af en ellipse Trin 2

2. Find den mindste radius. Som du måske har gættet, er den mindste radius afstanden fra centrum til det nærmeste punkt på kanten. Vi kalder denne værdi b.

Denne radius er vinkelret på den største radius, men du behøver ikke at måle vinkler for dette problem.

Du kan også kalde denne radius for `den lille hovedakse`.

Billede med titlen Beregn arealet af en ellipse Trin 3

3. Gang med pi. Området af ellipsen er -en x b x. Da du multiplicerer to længdeenheder sammen, er dit svar et kvadrat.

For eksempel, hvis en ellipse har en største radius på 5 og en mindste radius på 3, så er arealet af ellipsen 3 x 5 x π, eller cirka 47 enheder i anden.

Hvis du ikke har en lommeregner, eller hvis din lommeregner ikke har et π-symbol, skal du bruge `3.14` som værdien for pi.

Del 2 af 2: Forstå hvorfor det virker

Billede med titlen Beregn arealet af en ellipse Trin 4

1. Overvej arealet af en cirkel. Du husker måske, at areal af en cirkel er lig med πr, hvilket er det samme som π x r x r. Antag, at vi vil bestemme arealet af en cirkel, som om det var en ellipse? Vi måler radius i én retning: r. Mål det med rette vinkler: også r. Anvend dette på formlen for arealet af en ellipse: π x r x r! Det viser sig, at en cirkel blot er en bestemt type ellipse.

Billede med titlen Beregn arealet af en ellipse Trin 5

2. Forestil dig en fladtrykt cirkel. Forestil dig, at en cirkel er trykt i form af en ellipse. Efterhånden som cirklen komprimeres længere og længere, vil den ene radius blive kortere og den anden længere. Området forbliver det samme, for intet går ud af cirklen. Så længe vi bruger begge radier i ligningen, vil `klemning` og `strækning` ophæve hinanden, og vi får stadig det rigtige svar.