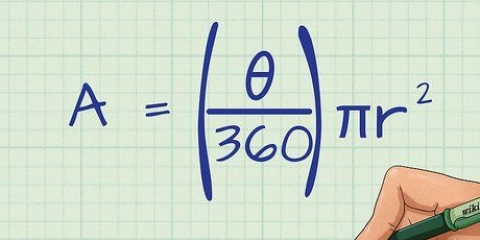Find arealet af en sfære: 8 trin (med billeder)

Indhold

Trin
Tips

Arealet af en kugle er antallet af kvadratenheder (cm, kvadratcentimeter eller meter – uanset hvad din måling er), der dækker ydersiden af en kugleformet genstand. Ligningen blev opdaget for tusinder af år siden af den græske filosof og matematiker Aristoteles og relativt enkel (selvom dens oprindelse ikke er det). For at finde arealet af en kugle, brug formlen (4πr), hvor r er radius af cirklen.

Trin

1. Kend delene af ligningen (Areal = 4πr). Denne gamle formel er stadig den nemmeste måde at bestemme arealet af en kugle på. Ved at bruge næsten enhver lommeregner kan du udfylde radius for at få arealet af din kugle.

r eller `radius:` Radius er afstanden fra kuglens centrum til kuglens kant.
π eller `pi:` Dette utrolige tal (svarende til omkring 3,14) repræsenterer forholdet mellem omkredsen og diameteren af en cirkel og er nyttig i alle ligninger, der involverer cirkler og kugler. Det forkortes normalt til π = 3,1416, men der er et uendeligt antal decimaler.
4: Af lidt komplicerede årsager er arealet af en kugle altid 4 gange arealet af en cirkel med samme radius.

Billede med titlen Find overfladearealet af en kugle Trin 2

2. Bestem kuglens radius. Nogle gange giver problemet dig strålen og andre gange skal du selv finde det. For at få diameteren af en cirkel skal du bare dividere diameteren med 2 for at få radius. For eksempel: en kugle med en diameter på 10 cm har en radius på 5 cm.

Tips til avancerede brugere: Hvis du kun kender volumen af en kugle, skal du arbejde lidt mere for at få radius. Divider volumen med 4π og gang svaret med 3. Tag endelig terningroden af dette svar.

Billede med titlen Find overfladearealet af en kugle Trin 3

3. Kvadret radius ved at gange den med sig selv. Du kan gøre dette ved manuel multiplikation (5 = 5 x 5 = 25) eller ved at bruge din lommeregners kvadratfunktion (nogle gange omtalt som `x`).

Billede med titlen Find overfladearealet af en kugle Trin 4

4. Gang dette resultat med 4. Selvom du kan gange 4 eller pi først, er det generelt nemmere at starte med 4, fordi der ikke er nogen decimaler at gange endnu.

Hvis vores radius er 5, som ovenfor, står du tilbage med 4 x 25 x π eller 100π.

Billede med titlen Find overfladearealet af en kugle Trin 5

5. Gang resultaterne med pi (π). Hvis problemet taler om en `præcis værdi`, skriv symbolet π efter dit tal, og du er færdig. Ellers skal du bruge tilnærmelsen π=3,14 eller knappen π på din lommeregner.

100 x = 100 x 3,14

100π = 314

Billede med titlen Find overfladearealet af en kugle Trin 6

6. Glem ikke at skrive dine enheder efter det endelige svar. Det skal være tydeligt, om overfladen af din kugle er f.eks. 314 cm eller 314 km. Enheden skal skrives som "enhed", da dette betegner areal, også kendt som "kvadratiske enheder",

Det fulde svar for kuglen på billederne er: Areal = 314 enheder.

De enheder du bruger er altid de samme som dem, der bruges til at måle radius. Hvis radius er i meter, vil svaret også være i meter.

Avanceret tip: Vi firkanter enhederne, fordi arealet måler, hvor mange flade firkanter der passer på kuglens overflade. Antag, at vi måler øvelsesproblemet i cm. Det betyder, at vi på en kugle, hvor r=5, kunne passe 314 kvadrater på kuglens overflade, hvis siderne af hver firkant var 1 cm lange.

Billede med titlen Find overfladearealet af en kugle Trin 7

7. Øv med et eksempel. Hvis radius af en kugle er 7 cm, hvad er arealet af den kugle??

4πr

r = 7

4 x x 7

49 x 4 x

196π

Svar: Areal = 615,75 cm (kvadratcentimeter).

Billede med titlen Find overfladearealet af en kugle Trin 8

8. Forstå området. Arealet af en kugle er det område, der dækker ydersiden af kuglen - tænk på det som læderet på en fodbold eller jordens overflade. Da en kugle er buet, er det meget sværere at måle arealet af en kugle end af en kasse, så vi har brug for en ligning for at bestemme arealet.

Rotation af en cirkel om dens akse (midten) producerer en kugle. Tænk på at dreje en mønt på bordet, og hvordan den ser ud til at danne en kugle. Selvom det ikke vil blive forklaret her, er det her, vores sammenligning kommer fra.

Tips til avancerede brugere: Kugler har et mindre overfladeareal pr. volumen end nogen anden form - det betyder, at de kan rumme flere ting pr. overfladeareal end nogen anden form.

Tips

Hvis radius indeholder en kvadratrod, såsom 3 √ 5, skal du huske at inkludere begge koefficientkvadrater hvis at kvadratroden. (3 √ 5) bliver 9 x 5 = 45.