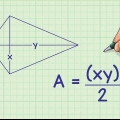
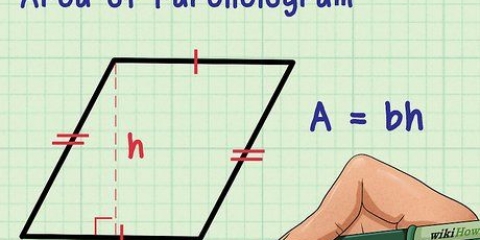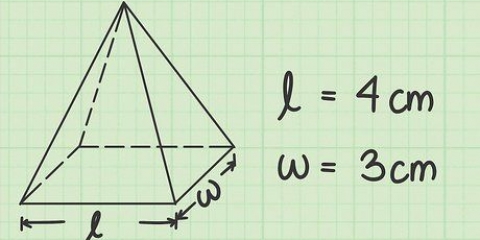For eksempel, hvis du vil finde arealet af en sekskantet pyramide, og du ved, at længden af den ene kant af basen er 4 cm, beregner du  at finde omkredsen af basen, fordi en sekskant har seks sider. Så omkredsen af basen er 24 cm, så formlen for området vil se sådan ud:
at finde omkredsen af basen, fordi en sekskant har seks sider. Så omkredsen af basen er 24 cm, så formlen for området vil se sådan ud:  .
. 
Antag, at skråhøjden af en sekskantet pyramide er 12 cm, så vil din formel se sådan ud:  .
. 
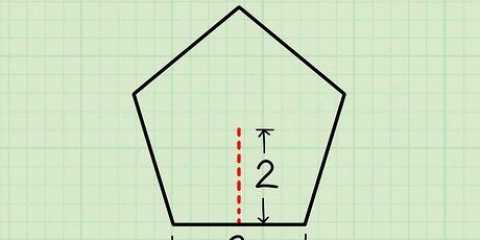
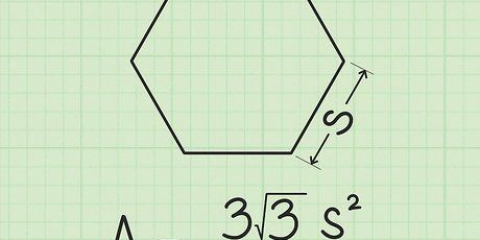
Hvis du for eksempel har at gøre med en sekskantet pyramide, skal du beregn arealet af sekskanten. Formlen er  , hvorved
, hvorved  er længden af den ene side af sekskanten. Da længden af den ene side af sekskanten er 4 cm, beregnes som følger:
er længden af den ene side af sekskanten. Da længden af den ene side af sekskanten er 4 cm, beregnes som følger:




 .
.
Så arealet af basen er 41,57 kvadratcentimeter. 
Antag, at arealet af den sekskantede base er 41,57 cm. så vil din formel for området se sådan ud:  .
. 
For eksempel:




For eksempel:


Så det samlede areal af en sekskantet pyramide, med en given basiskantlængde på 4 cm og en hældningshøjde på 12 cm, er lig med 185,57 kvadratcentimeter. 

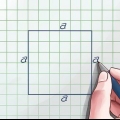
Antag, at længden af den ene side af bunden af en firkantet pyramide er 4 cm og hældningshøjden er 12 cm, så vil formlen se sådan ud:  .
. 
For eksempel:



For eksempel:





For eksempel:


Det samlede areal af en firkantet pyramide, med en side af bunden på 4 cm og en skrå højde på 12 cm, er derfor 112 kvadratcentimeter.
Bestemmelse af arealet af en pyramide
Indhold
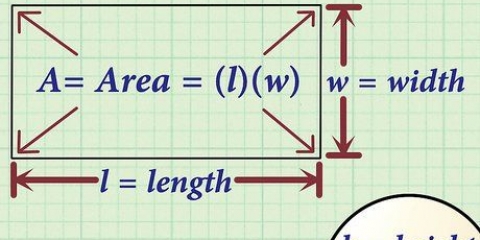
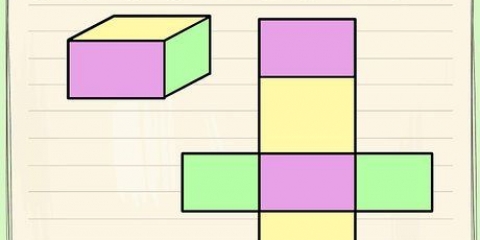
Arealet af en pyramide kan findes ved at lægge arealet af dens base til arealet af dens sider. Når du arbejder med almindelige pyramider, kan du finde området ved hjælp af en formel, så længe du ved, hvordan du finder arealet af bunden af pyramiden. Da basen kan være en polygon, er det nyttigt at vide, hvordan man bestemmer arealet af former som femkanter og sekskanter. Men når man arbejder med den almindelige almindelige firkantede pyramide, er det let at beregne det samlede areal, forudsat at man kender pyramidens skrå højde og længden af den firkantede base.
Trin
Metode 1 af 2: Find arealet af en almindelig pyramide

1. Skriv formlen for arealet af en almindelig pyramide. Formlen er  , hvorved
, hvorved  er lig med det samlede areal af pyramiden,
er lig med det samlede areal af pyramiden,  er lig med omkredsen af basen,
er lig med omkredsen af basen,  er lig med pyramidens hældning, og
er lig med pyramidens hældning, og  er lig med arealet af basen.
er lig med arealet af basen.
 , hvorved
, hvorved  er lig med det samlede areal af pyramiden,
er lig med det samlede areal af pyramiden,  er lig med omkredsen af basen,
er lig med omkredsen af basen,  er lig med pyramidens hældning, og
er lig med pyramidens hældning, og  er lig med arealet af basen.
er lig med arealet af basen. - Grundformlen for arealet af en pyramide, regulær eller uregelmæssig, er totalareal = basisareal + skrånende areal.
- Forveksle ikke `skrå højde` med `højde`.`Skråhøjden` er den diagonale afstand fra toppen af pyramiden til kanten af basen. `Højden` er den vinkelrette afstand fra top til base.

2. Beregn omkredsen af basen. Hvis omkredsen ikke er angivet, men er givet længden af en kant af basen, kan du beregne omkredsen ved at gange længden af en kant med antallet af kanter.
 at finde omkredsen af basen, fordi en sekskant har seks sider. Så omkredsen af basen er 24 cm, så formlen for området vil se sådan ud:
at finde omkredsen af basen, fordi en sekskant har seks sider. Så omkredsen af basen er 24 cm, så formlen for området vil se sådan ud:  .
.
3. Indtast hældningshøjdeværdien i formlen. Sørg for at bruge den skrå højde, ikke den vinkelrette højde. Hældningshøjden skal angives i opgaven. Hvis du ikke kender hældningshøjden, kan du ikke bruge denne metode.
 .
.
4. Beregn arealet af basen. Hvordan du gør dette afhænger af basens form. For det skal du vide hvordan man bestemmer arealet af polygoner.
 , hvorved
, hvorved  er længden af den ene side af sekskanten. Da længden af den ene side af sekskanten er 4 cm, beregnes som følger:
er længden af den ene side af sekskanten. Da længden af den ene side af sekskanten er 4 cm, beregnes som følger: 



 .
.Så arealet af basen er 41,57 kvadratcentimeter.

5. Anvend området af basen til formlen. Sørg for at have variablen  erstatter.
erstatter.
 erstatter.
erstatter. .
.
6. Multiplicer omkredsen af basen med den skrå højde af pyramiden. Divider produktet med to. Dette giver dig det skrånende område af pyramidens ansigter.




7. Læg de to værdier sammen. Summen er det skrå areal plus grundarealet, så du får det samlede areal af pyramiden i kvadratenheder.


Så det samlede areal af en sekskantet pyramide, med en given basiskantlængde på 4 cm og en hældningshøjde på 12 cm, er lig med 185,57 kvadratcentimeter.
Metode 2 af 2: Find arealet af en firkantet pyramide

1. Skriv formlen for arealet af en firkantet pyramide. Formlen er  , hvorved
, hvorved  er lig med længden af den ene side af basen, og
er lig med længden af den ene side af basen, og  er lig med pyramidens hældning.
er lig med pyramidens hældning.
 , hvorved
, hvorved  er lig med længden af den ene side af basen, og
er lig med længden af den ene side af basen, og  er lig med pyramidens hældning.
er lig med pyramidens hældning. - Forveksle ikke `skrå højde` med `højde`.`Skråhøjden` er den diagonale afstand fra toppen af pyramiden til kanten af basen. `Højden` er den vinkelrette afstand fra toppen til bunden.
- Bemærk, at denne formel blot er en anden måde at beregne Total Area = Basisareal (
) + Skrå overflade (
) at skrive. Denne formel virker kun for almindelige firkantede pyramider.

2. Indtast værdierne for siderelængden og hældningshøjden i formlen. Sørg for at erstatte længden af siden af basen med  og skråhøjden ved
og skråhøjden ved  .
.
 og skråhøjden ved
og skråhøjden ved  .
. .
.
3. Firkantet længden af den ene side af basen. Dette vil give dig arealet af basen.



4. Multiplicer længden af den ene side af basen med hældningshøjden og divider med to. Gang derefter med fire. Dette vil give dig den vinklede overflade af pyramiden.





5. Tilføj arealet af basen til det skrånende område. Dette vil give dig det samlede areal af pyramiden i kvadratiske enheder.


Det samlede areal af en firkantet pyramide, med en side af bunden på 4 cm og en skrå højde på 12 cm, er derfor 112 kvadratcentimeter.
Fornødenheder
- Blyant
- Papir
- Lommeregner (valgfrit)
- Lineal (valgfrit)
Artikler om emnet "Bestemmelse af arealet af en pyramide"
Оцените, пожалуйста статью
Lignende
Populær