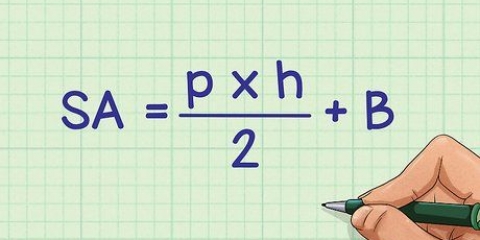Sådan beregnes volumen af en pyramide: 8 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Pyramide med rektangulær base
- Metode 2 af 2: Pyramide med en trekantet base
Tips
Advarsler

For at beregne rumfanget af en pyramide skal du gange arealet af basen med pyramidens højde. Divider resultatet med 3, det er alt! Læs denne artikel med beregningsmetoder for en pyramide med en rektangulær base og en pyramide med en trekantet base.

Trin

Metode 1 af 2: Pyramide med rektangulær base

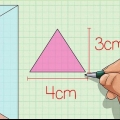
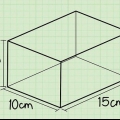
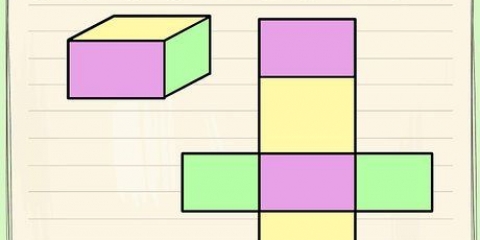
1. Bestem længden og bredden af basen. I dette eksempel er længden 4 cm og bredden 3 cm. Hvis du har en kvadratisk base, er metoden den samme, kun længden og bredden er ens. Skriv dine mål ned.

Billede med titlen Beregn volumen af en pyramide Trin 2

2. Multiplicer længden med bredden for at beregne arealet af basen. For at beregne arealet af vores eksempel multiplicerer vi 3 cm med 4 cm. 3 cm x 4 cm = 12 cm

Billede med titlen Beregn volumen af en pyramide Trin 3

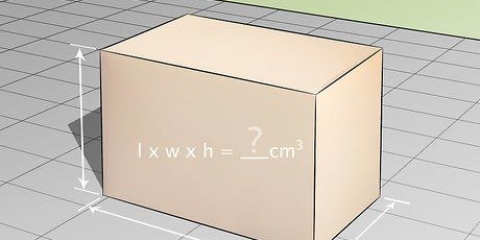
3. Multiplicer arealet af basen med højden. Arealet af basen er 12 cm og højden er 4 cm, så vi gange 12 cm med 4 cm. 12 cm x 4 cm = 48 cm

Billede med titlen Beregn volumen af en pyramide Trin 4

4. Divider resultatet med 3. Det er det samme som at gange med 1/3. 48cm/3 = 16cm. Rumfanget af en pyramide med en højde på 4 cm og en rektangulær base med en bredde på 3 cm og en længde på 4 cm er derfor 16 cm. Glem ikke at angive resultatet i kubikenheder.

Metode 2 af 2: Pyramide med en trekantet base

Billede med titlen Beregn volumen af en pyramide Trin 5

1. Bestem længden og bredden af basen. Basens længde og bredde skal vinkelret på hinanden, ellers vil denne metode ikke fungere. De kan også ses som bunden og højden af trekanten. I dette eksempel er trekantens bredde 2 cm og længden 4 cm. Skriv dette ned.

Billede med titlen Beregn volumen af en pyramide Trin 6

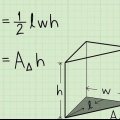
2. Beregn arealet af basen. For at beregne arealet af basen bruger vi følgende formel:A = 1/2(o)(h). Det her er sådan vi gør det:

A = 1/2(o)(h)

A = 1/2(2)(4)

A = 1/2(8)

A = 4 cm

Billede med titlen Beregn volumen af en pyramide Trin 7

3. Multiplicer arealet af basen med pyramidens højde. Basens areal er 4 cm, og højden er 5 cm. 4 cm x 5 cm = 20 cm.

Billede med titlen Beregn volumen af en pyramide Trin 8

4. Divider resultatet med 3. 20cm/3 = 6,67cm. Rumfanget af en pyramide med en højde på 5 cm og en trekantet base med en bredde på 2 cm og en længde på 4 cm er derfor 6,67 cm.

Tips

I en pyramide med kvadratisk base er højden, linjen, der deler den trekantede side i to lige store trekanter, og basens bredde forbundet med Pythagoras sætning: (bredde ÷ 2) + (højde) = (trekantens højde)
Denne metode kan også anvendes på objekter såsom femkantede pyramider, sekskantede pyramider osv. Den generelle proces er: A) beregn arealet af basen; B) mål højden fra toppen af pyramiden til midten af basen; C) gange A med B; D) dividere med 3.
I alt almindelig pyramider er de opretstående ribber, linjen der deler den trekantede side i to lige store trekanter og bredden af basen forbundet med Pythagoras sætning: (længde af siden ÷ 2) + (længde af ribben) = (højde)

Advarsler

Pyramider har tre typer højder: linjen, der deler den trekantede flade i to lige store trekanter, længden af ribben (langs siden af en trekantet flade) og den faktiske højde (fra spidsen af pyramiden vinkelret ned til bunden) . ).