Beregning af volumen af et trekantet prisme: 4 trin (med billeder)

Indhold

Trin
Tips

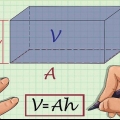
I geometri mener vi med et trekantet prisme et tresidet polyeder med to parallelle trekantede baser og tre rektangulære sider, ikke at forveksle med en pyramide. For at beregne volumenet af et trekantet prisme skal du først bestemme arealet af en base og gange det med prismets højde. I denne artikel kan du læse, hvordan du gør det.

Trin

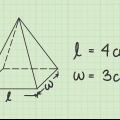
1. Find bunden og højden af en af de trekantede baser. De trekantede baser af det trekantede prisme har samme størrelse, så det er lige meget, hvilken trekant du bruger. Bestem nu trekantens base og højde ved at bestemme længden af en af trekantens sider. Find højden af trekanten ved at finde længden af en linje vinkelret på denne base. Hvis du arbejder med en retvinklet trekant, skal du blot tage længden af de to sider, der er vinkelrette på hinanden.

Antag, at vi har en trekant med en højde på 3 cm og en base på 4 cm.

Billede med titlen Beregn volumen af et trekantet prisme Trin 2

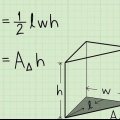
2. Multiplicer længden af basen med højden. Det er det første trin i at bestemme arealet af basen; i tilfælde af et trekantet prisme, det er en trekant. Altså: 3 cm x 4 cm = 12 cm. Glem ikke at angive resultatet i kvadratcentimeter, for du arbejder med overfladeareal.

Billede med titlen Beregn volumen af et trekantet prisme Trin 3

3. Divider resultatet med to. For at finde arealet af denne trekantede base skal du dividere 12 cm med 2. Altså: 12 cm/2 = 6 cm.

Billede med titlen Beregn volumen af et trekantet prisme Trin 4

4. Multiplicer dette tal med højden af polyederet. Antag, at højden af det trekantede prisme, eller længden af en af dets sider, er 10 cm. Derefter gange vi 6 cm med 10 cm for at finde rumfanget af det trekantede prisme. 6 cm x 10 cm = 60 cm. Glem ikke at skrive resultatet i kubikenheder; du arbejder med indhold.

Du har lige fulgt den enkle formel til at bestemme volumenet af et trekantet prisme: 1/2 x bh x l.

Tips

Med alt normal pyramider er diagonalen af basen, ribberne og højden forbundet med hinanden ved hjælp af Pythagoras sætning: (diagonal af basen/2)+ (højde)= (ribbens længde).