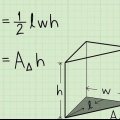
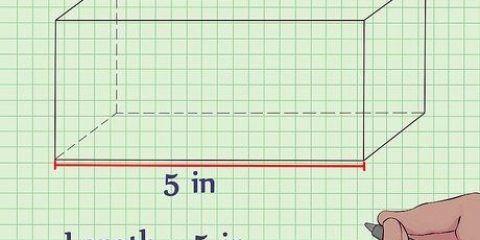
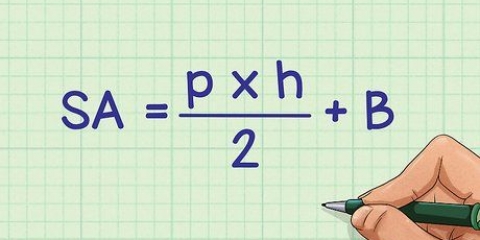I eksemplet er siderne af bunden af pyramiden alle 5 cm, og du beregner arealet af bunden som følger: 
Husk at todimensionelle områder er udtrykt i kvadrater – kvadratcentimeter, meter, kilometer osv. 
I eksemplet antager vi, at pyramiden har en højde på 9 cm. I dette tilfælde skal du gange arealet af basen med denne værdi, som følger: 
Husk at volumen er udtrykt i kubikenheder. I dette tilfælde, fordi alle lineære mål er centimeter, er volumen angivet i kubikcentimeter. 
I eksemplet divideres 225 cm med 3, og svaret er 75 cm for volumen. 


Denne udskiftning ser sådan ud: 


 .....(oprindelig ligning)
.....(oprindelig ligning) .....(firkant på begge sider)
.....(firkant på begge sider) .....(indtast værdier)
.....(indtast værdier) .....(forenkle brøk)
.....(forenkle brøk) .....(forenkle firkantet)
.....(forenkle firkantet) .....(trække fra)
.....(trække fra) .....(forenkle root)
.....(forenkle root)
Ud fra beregningerne udleder vi, at pyramidens højde er 12 cm. Brug dette sammen med 10 cm-siden af basen til at beregne pyramidens rumfang: 









 ..........(justeret ligning)
..........(justeret ligning) ..........(erstat h på begge sider)
..........(erstat h på begge sider) ..........(træk kvadratroden fra begge sider fra)
..........(træk kvadratroden fra begge sider fra) ..........(udfyld tallene)
..........(udfyld tallene) ..........(forenkle firkanterne)
..........(forenkle firkanterne) ..........(træk værdier fra)
..........(træk værdier fra) ..........(forenkle kvadratroden)
..........(forenkle kvadratroden)Fordoble denne værdi for at finde diagonalen af pyramidens kvadratiske base. Således er diagonalen af bunden af pyramiden 9,8 * 2 = 19,6 cm. 
I dette pyramideeksempel er bundens diagonal 19,6 cm. Derfor er siden lig med: 





Beregning af rumfanget af en firkantet pyramide
Indhold
En firkantet pyramide er en tredimensionel figur med en firkantet base og trekantede skråninger, der mødes på et punkt over basen. I tilfælde af at 


Trin
Metode 1 af 3: Bestem volumenet med arealet af basen og højden

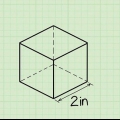
1. Mål længden af siden af basen. Da firkantede pyramider per definition har en kvadratisk base, bør alle sider af basen have samme længde. Så med en firkantet pyramide behøver du kun at kende længden af en af siderne.
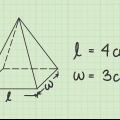
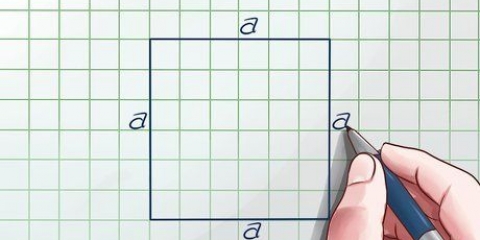
- Antag, at du har en pyramide med en firkantet base, hvis sider har en længde på
. Du vil bruge denne værdi til at beregne arealet af basen.
- Hvis siderne af basen ikke er lige lange, så har du en rektangulær pyramide i stedet for en firkantet pyramide. Formlen for rumfanget af en rektangulær pyramide ligner meget formlen for firkantede pyramider. I tilfælde af at
er længden af bunden af den rektangulære pyramide og
bredden, derefter pyramidens rumfang
.

2. Beregn arealet af basen. For at bestemme volumen skal du først bruge området af basen. Det gør du ved at gange længden og bredden af basen. Da bunden af en firkantet pyramide er en firkant, har alle sider den samme længde, og arealet af bunden er lig med kvadratet på længden af en af dens sider (altså ganget med sig selv).


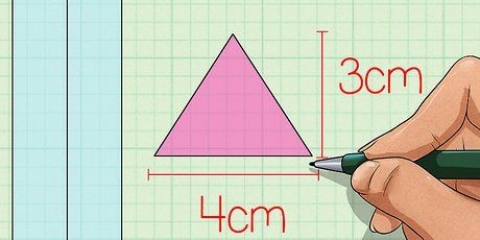
3. Multiplicer arealet af basen med pyramidens højde. Derefter gange du grundfladen med pyramidens højde. Som en påmindelse er højden afstanden er længden af linjestykket fra toppen af pyramiden til bunden, i rette vinkler.


4. Divider dette svar med 3. Til sidst bestemmer du pyramidens rumfang ved at dividere den værdi, du lige har fundet (ved at gange arealet af basen med højden) med 3. Dette beregner rumfanget af den firkantede pyramide.
Metode 2 af 3: Bestem rumfanget med apotemet

1. Mål pyramidens apotem. Nogle gange er pyramidens vinkelrette højde ikke angivet (eller du skal måle den), men apotemet. Med apotemet kan du bruge Pythagoras sætning bruges til at beregne vinkelret højde.
- Apotem af en pyramide er afstanden fra spidsen til midten af en af siderne af dens base. Mål til midten af en af siderne og ikke til et af hjørnerne af basen. For dette eksempel antager vi, at apotem er 13 cm og længden af den ene side af basen er 10 cm.
- Husk, at Pythagoras sætning kan udtrykkes som ligningen
, hvorved
og
de vinkelrette ben er af den rette trekant og
hypotenusen.

2. Forestil dig en retvinklet trekant. For at bruge Pythagoras sætning skal du bruge en retvinklet trekant. Forestil dig en trekant, der deler pyramiden i to og vinkelret på bunden af pyramiden. Pyramidens apotem, kaldet  , er hypotenusen af denne retvinklede trekant. Basen af denne retvinklede trekant er halvdelen af længden af
, er hypotenusen af denne retvinklede trekant. Basen af denne retvinklede trekant er halvdelen af længden af  , siden af pyramidens firkantede base.
, siden af pyramidens firkantede base.
 , er hypotenusen af denne retvinklede trekant. Basen af denne retvinklede trekant er halvdelen af længden af
, er hypotenusen af denne retvinklede trekant. Basen af denne retvinklede trekant er halvdelen af længden af  , siden af pyramidens firkantede base.
, siden af pyramidens firkantede base.
3. Tildel variabler til værdierne. Pythagoras sætning bruger variablerne a, b og c, men det er nyttigt at erstatte dem med variabler, der er meningsfulde for dit problem. apotemet  træder i stedet for
træder i stedet for  i Pythagoras sætning. Benet af den retvinklede trekant (
i Pythagoras sætning. Benet af den retvinklede trekant ( ), træder i stedet for
), træder i stedet for  Du går i højden
Du går i højden  bestemme pyramiden, som indtager pladsen
bestemme pyramiden, som indtager pladsen  i Pythagoras sætning.
i Pythagoras sætning.
 træder i stedet for
træder i stedet for  i Pythagoras sætning. Benet af den retvinklede trekant (
i Pythagoras sætning. Benet af den retvinklede trekant ( ), træder i stedet for
), træder i stedet for  Du går i højden
Du går i højden  bestemme pyramiden, som indtager pladsen
bestemme pyramiden, som indtager pladsen  i Pythagoras sætning.
i Pythagoras sætning.


4. Brug Pythagoras sætning til at beregne den vinkelrette højde. Brug de målte værdier  og
og  . Løs derefter ligningen:
. Løs derefter ligningen:
 og
og  . Løs derefter ligningen:
. Løs derefter ligningen: .....(oprindelig ligning)
.....(oprindelig ligning) .....(firkant på begge sider)
.....(firkant på begge sider) .....(indtast værdier)
.....(indtast værdier) .....(forenkle brøk)
.....(forenkle brøk) .....(forenkle firkantet)
.....(forenkle firkantet) .....(trække fra)
.....(trække fra) .....(forenkle root)
.....(forenkle root)
5. Brug højde og base til at beregne volumen. Efter at have anvendt disse beregninger på Pythagoras sætning har du nu den information, du har brug for til at beregne volumen af pyramiden. Brug formlen  og løs disse, og sørg for at give svaret i kvadratiske enheder.
og løs disse, og sørg for at give svaret i kvadratiske enheder.
 og løs disse, og sørg for at give svaret i kvadratiske enheder.
og løs disse, og sørg for at give svaret i kvadratiske enheder.



Metode 3 af 3: Bestemmelse af volumen med højden af benene

1. Mål højden af pyramidens ben. Højden på benene er længden af pyramidens kanter, målt fra toppen til et af hjørnerne af basen. Som ovenfor, brug Pythagoras sætning til at beregne den vinkelrette højde af pyramiden.
- I dette eksempel antager vi, at højden på benene er 11 cm, og at den vinkelrette højde er 5 cm.

2. Forestil dig en retvinklet trekant. Igen skal du bruge en retvinklet trekant for at kunne bruge Pythagoras sætning. I dette tilfælde er den ukendte værdi dog bunden af pyramiden. Kendt er den lodrette højde og højden af benene. Forestil dig nu at skære pyramiden diagonalt fra det ene hjørne til det andet, og derefter åbne figuren, det resulterende fly vil ligne en trekant. Højden af den trekant er den vinkelrette højde af pyramiden. Dette opdeler den blotlagte trekant i to symmetriske retvinklede trekanter. Hypotenusen af hver af de rette trekanter er højden af pyramidens ben. Grundlaget for hver af de retvinklede trekanter er halvdelen af diagonalen af bunden af pyramiden.

3. Tildel variabler. Brug den imaginære retvinklede trekant og tildel værdier til Pythagoras sætning. Du kender den lodrette højde,  som er den ene side af Pythagoras sætning,
som er den ene side af Pythagoras sætning,  . Højden af pyramidens ben,
. Højden af pyramidens ben,  danner hypotenusen af denne imaginære retvinklede trekant og træder derfor i stedet for
danner hypotenusen af denne imaginære retvinklede trekant og træder derfor i stedet for  . Den ukendte diagonal af bunden af pyramiden er den resterende side af den retvinklede trekant,
. Den ukendte diagonal af bunden af pyramiden er den resterende side af den retvinklede trekant,  Efter at have foretaget disse substitutioner ser ligningen sådan ud:
Efter at have foretaget disse substitutioner ser ligningen sådan ud:
 som er den ene side af Pythagoras sætning,
som er den ene side af Pythagoras sætning,  . Højden af pyramidens ben,
. Højden af pyramidens ben,  danner hypotenusen af denne imaginære retvinklede trekant og træder derfor i stedet for
danner hypotenusen af denne imaginære retvinklede trekant og træder derfor i stedet for  . Den ukendte diagonal af bunden af pyramiden er den resterende side af den retvinklede trekant,
. Den ukendte diagonal af bunden af pyramiden er den resterende side af den retvinklede trekant,  Efter at have foretaget disse substitutioner ser ligningen sådan ud:
Efter at have foretaget disse substitutioner ser ligningen sådan ud:


4. Beregn diagonalen af kvadratbasen. Du skal omarrangere ligningen for at få variablen  isolere, og beregn derefter dens værdi.
isolere, og beregn derefter dens værdi.
 isolere, og beregn derefter dens værdi.
isolere, og beregn derefter dens værdi. ..........(justeret ligning)
..........(justeret ligning) ..........(erstat h på begge sider)
..........(erstat h på begge sider) ..........(træk kvadratroden fra begge sider fra)
..........(træk kvadratroden fra begge sider fra) ..........(udfyld tallene)
..........(udfyld tallene) ..........(forenkle firkanterne)
..........(forenkle firkanterne) ..........(træk værdier fra)
..........(træk værdier fra) ..........(forenkle kvadratroden)
..........(forenkle kvadratroden)
5. Find siden af bunden af diagonalen. Pyramidens bund er en firkant. Diagonalen af hvert kvadrat er lig med længden af en af dets sider, gange kvadratroden 2. Og så kan du finde siden af et kvadrat ved at dividere diagonalen med kvadratroden 2.


6. Beregn volumen ved hjælp af siden og højden. Vend tilbage til den oprindelige formel for at beregne volumen ved hjælp af side og vinkelret højde.




Tips
- I en kvadratisk pyramide kan den vinkelrette højde, apotem og længden af kanten af basen alle beregnes ved hjælp af Pythagoras sætning.
Artikler om emnet "Beregning af rumfanget af en firkantet pyramide"
Оцените, пожалуйста статью
Lignende
Populær