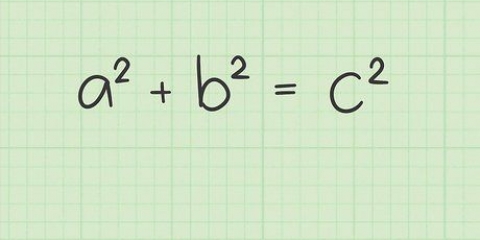Antag, at vi ved, at hypotenusen har en længde på 5 og en af de andre sider har en længde på 3. Længden af den resterende side er ukendt. Da to af siderne er kendte, kan vi fortsætte med at beregne længden af den ukendte side! Vi vil bruge dette eksempel igen senere. Hvis længden af to af siderne er ukendte, så skal du bestemme længden af mindst en side mere for at kunne bruge Pythagoras sætning. De grundlæggende trigonometriske funktioner kan hjælpe dig med dette, forudsat at du kender en af trekantens andre ikke-rette vinkler. 
I vores eksempel kender vi længden af den ene side og længden af hypotenusen (3 & 5), så vi skriver vores ligning sådan: 3² + b² = 5² 
I vores eksempel firkanter vi 3 og 5 for at få hhv. 9 og 25 at få. Vi kan nu omskrive ligningen til 9 + b² = 25. 
I vores eksempel er ligningen nu 9 + b² = 25. til b² trækker vi 9 fra begge sider af ligningen. Dette efterlader os med b² = 16. 
I vores eksempel, b² = 16, er ligningen efter at have taget kvadratrødder b = 4. Så vi kan sige, at længden af den ukendte side af vores trekant er lig med 4. 
Lad os tage et eksempel fra den virkelige verden. En stige læner sig op ad en væg. Bunden af stigen er 5 meter væk fra væggen. Stigen kommer op til 20 meter målt fra bunden af væggen. Hvor lang er stigen? "5 meter er afstanden til væggen” og "stigen er 20 meter høj”. Dette giver en indikation af længden af trekantens sider. Da væggen og jorden formodes at danne en ret vinkel, og stigen er diagonal på væggen i en vinkel, kan vi betragte dette arrangement som en retvinklet trekant, hvis sider har en længde på a = 5 og b = 20. Længden af stigen er hypotenusen, den ukendte variabel c. Lad os anvende Pythagoras sætning her: a² + b² = c² (5)² + (20)² = c² 25 + 400 = c² 425 = c² sqrt(425) = c c = 20,6 . Længden af stigen er (ca.) 20,6 meter. 


Antag, at vi har punkterne (6.1) og (3.5). Længden af den vandrette side af vores trekant er: |x1 - x2| |3 - 6| | -3 | = 3 Længden af den lodrette side er: |y1 - y2| |1 - 5| | -4 | = 4 Så vi kan sige, at længden af siderne i vores retvinklede trekant er lig med a = 3 og b = 4. 
I vores eksempel kender vi punkterne (3,5) og (6.1), og længderne af siderne er a= 3 og b=4, så vi bestemmer hypotenusen som følger: sqrt(x) betyder "kvadratroden af x". Glem ikke altid at tjekke dine svar. Hvis det ser ud til, at et svar ikke er rigtigt, så tjek dine beregninger eller start forfra. Hvis du kun kender den ene side af trekanten, men også en af de andre vinkler (end den rette vinkel), skal du først beregne en anden side ved at bruge det, du ved om trigonometri (sin, cos, tan) eller proportionerne 30-60- 90 / 45-45-90. En anden kontrol - den længste side modsætter den største vinkel og den korteste side modsætter den mindste vinkel.
Brug af pythagoras sætning
Indhold
Pythagoras sætning beskriver længden af siderne i en retvinklet trekant på en måde så elegant og praktisk, at den stadig er meget udbredt i dag. Dette angiver, at for enhver retvinklet trekant er summen af kvadraterne på de rigtige sider lig med kvadratet på hypotenusen. Med andre ord, for en retvinklet trekant (en trekant med sider, der er vinkelrette på hinanden), med sider af længden a og b og en hypotenus med længden c: a + b = c. Pythagoras sætning er en af geometriens søjler og har adskillige praktiske anvendelser – for eksempel ved hjælp af denne sætning er det meget nemt at finde afstanden mellem to punkter i et plan.
Trin
Metode 1 af 2: Længden af siderne i en retvinklet trekant

1. Tjek, om du har med en retvinklet trekant at gøre. Pythagoras sætning kan kun bruges til retvinklede trekanter, så inden du fortsætter er det vigtigt at fastslå, at din trekant opfylder definitionen af en retvinklet trekant. Heldigvis er der kun én afgørende faktor her – et af trekantens hjørner skal være en 90 graders vinkel.
- Et fingerpeg er, at rette vinkler ofte er markeret med en lille firkantet parentes for at angive, at dette er en 90 graders vinkel. Se om der er sådan et beslag i et af hjørnerne af din trekant.

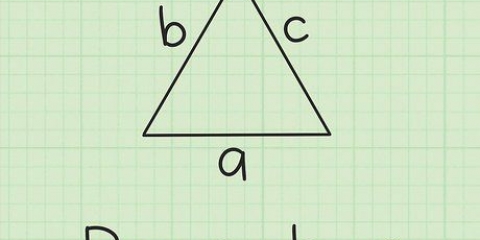
2. Tildel variablerne a, b og c til siderne af din trekant. I Pythagoras sætning refererer variablerne a og b til de rigtige sider af din trekant, og variablen c til hypotenusen - den lange side modsat den rette vinkel. Så til at starte med tildeler du variablerne a og b (rækkefølgen er ligegyldig) til de lige sider, og du tildeler c til hypotenusen.

3. Bestem hvilken side af trekanten du vil vide. Pythagoras sætning giver dig mulighed for at finde længden af enhver side i en trekant, forudsat at to af siderne er kendt. Bestem, hvilken af siderne der har en ukendt længde---en, b, og/ellerc. Hvis kun én er ukendt, så kan du komme videre.

4. Beregn ved hjælp af ligningen og de kendte. Indsæt værdierne for længderne af siderne af din trekant i ligningen a + b = c. Husk at a og b er de lige sider og c er hypotenusen.

5. Beregn firkanterne. For at løse din ligning, start med at kvadrere hver af de kendte sider. Hvis du finder det nemmere, kan du lade kraften stå og vende den senere.

6. Isoler den ukendte variabel på den ene side af lighedstegnet. Brug eventuelt standard algebraiske operationer til at få det ukendte til den ene side af lighedstegnet og kvadraterne til den anden side. Hvis du forsøger at finde hypotenusen, er c allerede i positionen på den ene side, så du kan springe det trin over.

7. Tag kvadratroden af begge sider af ligningen. Du skal nu have et kvadrat (variabel) på den ene side af ligningen og et tal på den anden side. Træk nu kvadratroden af begge sider for at finde længden af det ukendte.

8. Brug Pythagoras sætning i praksis. Grunden til at Pythagoras sætning bruges så meget, er fordi den er anvendelig til at løse mange praktiske problemer. Lær at genkende retvinklede trekanter i verden omkring dig – hvor end du kan identificere en retvinklet trekant med et eller flere objekter, kan Pythagoras sætning bruges til at finde længden af en af siderne, forudsat at der er to sider eller vinkler.
Metode 2 af 2: Beregn afstanden mellem to punkter i planet

1. Definer to punkter i planet. Pythagoras sætning kan meget let bruges til at bestemme afstanden i en ret linje mellem to punkter i planet. Alt du behøver er x- og y-koordinaterne for to punkter. Normalt skrives disse koordinater som (x, y).
- For at finde afstanden mellem disse to punkter betragter vi hvert af punkterne som et af hjørnerne i en retvinklet trekant, som ikke hører til den rette vinkel. Dette gør det meget nemt at finde længden af a og b, hvorefter c (hypotenusen og afstanden mellem de to punkter) kan beregnes.

2. Tegn de to punkter på en graf. I et X-Y-plan, for hvert punkt (x, y), er x et punkt på den vandrette x-akse, og y er et punkt på den lodrette y-akse. Du kan finde afstanden mellem de to uden at tegne dem, men hvis du gør det, får du en visuel reference for at kontrollere, om dit svar giver mening.

3. Find længden af de lige sider af din trekant. Ved at betragte dine to punkter som vinklerne på trekanten, der støder op til hypotenusen, kan du finde længderne af siderne a og b. Du kan gøre dette ved at bruge diagrammet eller ved at bruge formlerne |x1 - x2| for den vandrette side og |y1 - y2| for den lodrette side, hvor (x1,y1) er det første punkt og (x2,y2) det andet punkt.

4. Brug Pythagoras sætning til at finde hypotenusen. Afstanden mellem de to punkter er længden af trekantens hypotenus. Brug Pythagoras sætning til at finde hypotenusen i trekanten med siderne a, b og c.
- (3)²+(4)²= c²
- c= sqrt(9+16)
- c= sqrt(25)
- c=5. Afstanden mellem (3.5) og (6.1) er 5.
Tips
- Hvis trekanten ikke er en retvinklet trekant, så kan man ikke bare bruge Pythagoras sætning.
- Hypotenusen er altid:
- linjen modsat den rette vinkel
- den længste side af den retvinklede trekant
- variablen c i Pythagoras sætning
Artikler om emnet "Brug af pythagoras sætning"
Оцените, пожалуйста статью
Populær