Brug af hældningsformlen

Indhold

Trin
Tips

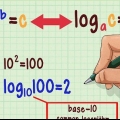
Hældningsformlen er en almindelig måde at skrive en lineær ligning på. Denne formel er skrevet som "y = mx + b" – hvor bogstaverne får en bestemt værdi for at kunne løse denne ligning, eller hvor ligningen er løst for at finde variablernes værdier. Så: "x" og "y" er "x-" og "y"-koordinater for en linje, "m" er hældningen (hældningen), forholdet (ændring af y)/(ændring af x), og "b" er skæringspunktet med y-aksen. Hvis du vil vide, hvordan du bruger hældningsformlen, er du kommet til det rigtige sted.

Trin

Metode 1 af 5: Brug hældningsformlen til problemer

1. Læs opgaven. Inden du kan gå videre, skal du læse opgaven grundigt igennem, så du helt præcist forstår, hvad der bliver bedt om af dig. Læs følgende udtalelse: Din bankkonto stiger lineært hver uge. Hvis du har 560 USD på din bankkonto efter 20 ugers arbejde og 585 USD efter 21 uger, hvordan udtrykker du så forholdet mellem det beløb, du tjente, og hvor mange uger du arbejdede ved hjælp af hældningsformlen.

Billede med titlen Brug Slope Intercept Form (i Algebra) Trin 2

2. Tænk på problemet i form af hældningsformlen. Du skal skrive det ned sådan her: y = mx + b. Variablen "m" er hældningen og "b" er udgangspunktet, hvor linjen skærer y-aksen. Bemærk, at problemet angiver det, " Din bankkonto stiger lineært hver uge," hvilket betyder, at du sparer det samme beløb hver uge, hvilket igen betyder, at du har en lige, skrå linje. At "konstant," og en jævn kontinuerlig opsparingsplan er det, der gør den lineær. Hvis du ikke sparer det samme beløb hver gang, er det ikke lineært.

Billede med titlen Brug Slope Intercept Form (i Algebra) Trin 3

3. Find linjens hældning. For at finde hældningen skal du være i stand til at bestemme ændringshastigheden. Hvis du starter med €560 og ugen efter har du €585, så har du tjent €25 efter 1 uges arbejde. Du kan også beregne dette ved at trække €560 fra €585. 585-560 = 25.

4. Find skæringspunktet med y-aksen. For at finde dette kryds, også kaldet "b" i y = mx + b skal du kende udgangspunktet for dit problem (det er skæringspunktet med y-aksen). Det betyder, at du skal finde ud af, hvor mange penge du startede med. Hvis du havde $560 efter 20 ugers arbejde, og du ved, at du tjente $25 på en uge, så brug følgende multiplikation til at beregne, hvor meget du tjente på 20 uger. 20 x 25 = 500, så du tjente 500 USD i disse uger.

For efter 20 uger har du €560 og også tjent €500. så ved du hvor meget du startede med at trække 500 fra 560. 560 - 500 = 60.

Så "b" eller udgangspunktet er 60.

5. Skriv ligningen. Nu hvor du kender hældningen, m er 25, (tjener 25 dollars om ugen), og startpunktet b er 60, kan du sætte dette ind i ligningen:

y = mx + b

y = 25x + 60

6. Test om ligningen er korrekt. Det "y" er det beløb, du har tjent og "x" antallet af uger du har arbejdet. Se hvor mange penge du har tjent på et givet antal uger ved at indtaste disse data i ligningen. Prøv to eksempler:

Hvor mange penge tjente du på 10 uger? fylde "10" ind for "x" at finde ud af her.

y = 25x + 60 =

y = 25(10) + 60 =

y = 250 + 60 =

y = 310. Efter 10 uger har du tjent €310.

Hvor mange uger skal du arbejde for at tjene 800 euro? fylde "800" ind for "y"-variabel af ligningen for at komme bag ved værdien af "x" at komme.

y = 25x + 60 =

800 = 25x + 60 =

800 - 60 =

25x = 740 =

25x/25 = 740/25 =

x = 29.6. Du kan tjene 800 euro på cirka 30 uger.

Metode 2 af 5: Konvertering af en ligning til hældningsformlen

1. Skriv ligningen. Antag, at du har at gøre med følgende ligning, 4y +3x = 16.

2. Isoler y-leddet på den ene side af ligningen. Det gør du ved at trække 3x fra begge sider af ligningen. Ligningen skulle nu se sådan ud: 4y = -3x +16.

4y + 3x = 16

4y + 3x - 3x = 16 -3x

4y = -3x +16

3. Divider alle led med koefficienten y. Dette er tallet for y-variablen. Læg ikke et tal her, så er du færdig. Hvis der er et tal (koefficienten), divider du hvert led i ligningen med det tal. I dette tilfælde er y-koefficienten 4, så du skal dividere 4x, -3x og 16 med 4 for at få det endelige svar. Sådan fungerer det:

4y = -3x +16 =

/₄y = /₄x +/_{4 = (ved division)}

y = /₄x + 4 (ved at forenkle opdelingen)

4. Bestem vilkårene i ligningen. Når du bruger ligningen til at tegne en linje, så husk det "y" y-koordinaten er en "-3/4" skråningen eller skråningen, "x" er så x-koordinaterne og "4" skæringen med y-aksen.

Metode 3 af 5: Hældningsformlen ved hjælp af et punkt og hældningen

1. Skriv linjens ligning som hældningsformlen. Bare skriv først y = mx + b. Du kan derefter udfylde ligningen, når du har nok data. Antag, at du vil løse følgende problem: Find ligningen for en linje med en hældning på 4, der går gennem punktet (-1, -6).

2. Udfyld detaljerne. Du ved det "m" er lig med hældningen af linjen, er lig med 4 og det "y" og "x" henholdsvis "x" og "y" koordinater er. I dette tilfælde er dataene "x" = -1 og "y" = -6. "b" repræsenterer skæringspunktet med y-aksen; denne værdi er endnu ikke kendt. Sådan ser ligningen ud nu:

y = -6, m = 4, x = -1 (de angivne værdier)

y = mx + b (formlen)

-6 = (4)(-1) + b (efter udfyldning)

3. Løs for "b". Nu gælder det om at træne "b," find skæringspunktet med y-aksen. Multiplicer 4 og -1 og træk derefter resultatet fra -6. Sådan gør du det:

-6 = (4)(-1) + b

-6 = -4 + b

-6 - (-4) = -4 -(-4) + b

-6 - (-4) = b (udtryk forenklet højre)

-2 = b (udtryk venstre forenklet)

4. Skriv ligningen. Din tur "b," du kan udfylde de nødvendige værdier i hældningsformlen. Alt du behøver at vide er hældningen og skæringspunktet med y-aksen (b):

m = 4, b = -2

y = mx + b

y = 4x -2 (substitution)

Metode 4 af 5: Nedskrivning af hældningsformlen ved hjælp af to punkter

1. Skriv de to punkter ned. Før du kan lave linjens ligning, skriver du først de to punkter ned, der er givet. Antag, at du vil løse følgende problem: Find ligningen for linjen gennem punkterne (-2, 4) og (1, 2).

2. Brug disse punkter til at finde hældningen af ligningen. Formlen til bestemmelse af linjens hældning gennem to punkter er (y₂ - y₁) / (x₂ - x₁). Du har at gøre med koordinaterne (x₁, Y₁) = (-2, 4) og (x₂, Y₂ ) = (1, 2). Indsæt nu denne værdi i ligningen og løs for m.

(y₂ - y₁) / (x₂ - x₁) =

(2 - 4)/(1 - -2) =

-2/3 = m

Linjens hældning er -2/3.

3. Vælg et af punkterne, der skal løses for skæringspunktet med y-aksen. Det er lige meget hvilket par du vælger. Vælg den, der er nemmest for dig at arbejde med Antag, at du vælger punktet (1, 2). Udfyld nu dette i ligningen "y = mx + b". Løs for "b":

y = 2, x, = 1, m = -2/3

y = mx + b

2 = (-2/3)(1) + b

2 = -2/3 + b

2 - (-2/3) = b

2 + 2/3 = b, eller b = /₃

4. Udfyldning af tallene i den oprindelige ligning. Nu hvor du ved, at hældningen er lig med 2/3 og skæringspunktet med y-aksen ("b") er lig med 2 2/3, du kan sætte disse værdier ind i linjens oprindelige ligning, og du er færdig.

y = mx + b

y = /₃x + 2 2/3

Metode 5 af 5: Tegning af linjen

1. Skriv ligningen og brug den til at tegne linjen. Antag at du har følgende ligning: y = 4x + 3.

2. Start med skæringspunktet med y-aksen. Skæringspunktet med y-aksen er givet ved "+3" eller "b" i ligningen. Dette er punktet (0, 3). Angiv dette punkt med en prik.

3. Brug linjens hældning til at finde koordinaterne for det andet punkt. Fordi du ved, at hældningen er repræsenteret ved "m=4," kan man sige, at hældningen er lig med y/x=4/1. Det betyder, at hver gang linjen stiger 4 punkter på y-aksen, skifter den 1 punkt til højre på x-aksen. Så du starter ved punkt (0, 3) og går 4 punkter op og 1 punkt til højre, og ender ved punkt (1, 7) som det næste punkt på linjen.

Hvis hældningen er negativ, går linjen ned fra venstre mod højre.

4. Forbind de to punkter med en linje. Brug en blyant og lineal til dette. Dette er alt, du skal gøre, og du har tegnet en perfekt linje i henhold til den givne ligning. To point er nok til at trække linjen. Tjek eventuelt ved at tegne et par punkter mere.

Tips

Et eksempel på lineær fald og stigning er den konstante ændring af et objekts hastighed, målt i meter per sekund, afstand målt over tid.
Algebra er aktiv. Man skal ikke bare læse og forstå teorien, man skal også arbejde med den for at forstå, hvordan den fungerer.
Dette er den rigtige måde at vise, at du forstår: Ændringen af y sammenlignet med ændringen af x kaldes stigningen (væksten) eller faldet (henfald) af forskellen på y divideret med forskellen på x. At dividere med kaldes også et forhold, brøk eller forhold. Her er forholdet "graden af forandring.
I starten skal du også udarbejde de simple øvelser på papir. Hvis du arbejder med sværere øvelser på et senere tidspunkt, vil du have meget gavn af denne metode, fordi den giver dig en bedre ide om proceduren for at lave en graf.
Husk: multiplikation kommer før addition, så y = mx + b; så først m ×x og derefter x+b.
Læs ikke bare eksemplerne. Skriv dem ned og øv de forskellige trin, så du forstår hele processen godt.
Du vil helt sikkert imponere din lærer, hvis du lærer at forstå, hvordan man anvender en lineær ligning på alle slags problemer.
Det kartesiske koordinatsystem brugt i algebra til at lave en graf osv. er opkaldt efter sin franske opfinder og bruger den til koordinater på kort. Lignende systemer bruges inden for forskellige områder af matematik, såvel som i astronomi, navigation, computerskærme, neonskilte og resultattavler eller til at lokalisere næsten alt.
Hældningen af en linje måler forholdet mellem den lodrette ændring (y) sammenlignet med den vandrette ændring (x). Det kan dreje sig om punkter på en linje, men også om en vis lineær væksthastighed eller hældningen af en bakke.