Rette vinkler er ofte angivet i lærebøger og prøver med en lille firkant i højre hjørne. Denne særlige mærkning betyder "90 grader." 
Hvis din trekant har siderne 3 og 4, og du har tildelt bogstaver til disse sider, så a = 3 og b = 4, regner du ligningen ud som: 3 + 4 = c. 
Hvis a = 3, a = 3 x 3 eller 9.Hvis b = 4, så er b = 4 x 4 eller 16. Når du indregner disse værdier i din ligning, skulle det nu se sådan ud: 9 + 16 = c. 
I vores eksempel, 9 + 16 = 25, tag da til efterretning 25 = c. 
I vores eksempel, c = 25.Kvadratroden af 25 er 5 (5 x 5 = 25, Så Sqrt(25) = 5).Og det betyder c = 5, længden af vores hypotenuse! 

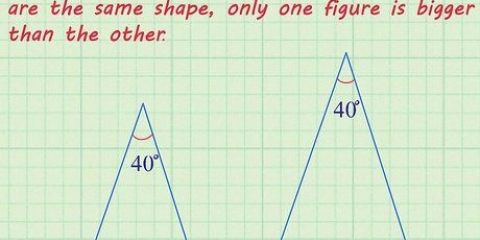
Du beregner hypotenusen af denne trekant baseret på længden af et af benene og gange dens længde med Sqrt(2). Det er nyttigt at kende dette forhold, især hvis dine test- eller lektierproblemer giver dig længden af sider i form af variable i stedet for heltal. 
Givet længden af det korteste ben (det modsat 30 graders vinkel), ganges længden af dette ben med 2 for at få længden af hypotenusen. For eksempel hvis længden af det korteste ben 4 er, så ved du, at hypotenusen 8 må være. Hvis du kender længden af det længere ben (modsat 60 graders vinkel), ganges denne længde med2/Sqrt(3) at finde længden af hypotenusen.For eksempel hvis længden af det korteste ben 4 er, så ved du, at hypotenusen 4,62 må være. 

For at finde sinus for en 80-graders vinkel, vil du synd 80 skal skrive efterfulgt af lighedstegnet eller Enter, eller80 synd. (Svaret er -0,9939.) Du kan også søge efter "synd lommeregner" med din browser for nogle letanvendelige lommeregnere, så du ikke behøver at gætte. 
Sinusreglen kan faktisk bruges til at løse for hver trekant, men kun en retvinklet trekant vil have en hypotenusa. 

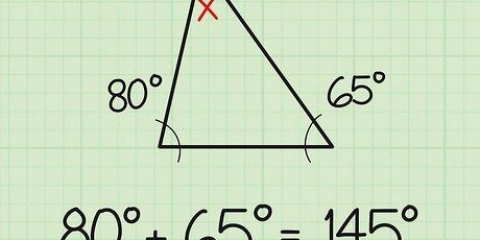
For eksempel hvis du ved det A = 40 grader, derefter B = 180 – (90 + 40). Forenkle dette til B = 180 – 130 og det kan du hurtigt udlede B = 50 grader. 
For at fortsætte med vores eksempel, lad os sige, at længden af side a = 10.Vinkel C = 90 grader, vinkel A = 40 grader og vinkel B = 50 grader. 

Ud fra vores eksempel ser vi det synd 40 = 0,64278761.For at finde værdien af c dividerer vi længden af a med dette tal og finder det 10 / 0,64278761 = 15,6, længden af vores hypotenuse!
Bestemmelse af længden af hypotenusen
Indhold
Alle rette trekanter har en ret vinkel (på 90 grader), og hypotenusen er siden modsat denne vinkel. Hypotenusen er den længste side af trekanten, og den er også meget nem at finde ved hjælp af en række forskellige metoder. Denne artikel vil lære dig, hvordan du bestemmer længden af hypotenusen ved hjælp af Pythagoras sætning, forudsat at du kender længden af de to andre sider af trekanten. Så lærer du at beregne hypotenusen af nogle specielle retvinklede trekanter, som du ofte vil støde på i tests. Og endelig vil du lære at beregne længden af hypotenusen ved hjælp af sinusreglen, når kun længden af en af siderne er kendt og størrelsen af en af vinklerne.
Trin
Metode 1 af 3: Brug af Pythagoras sætning

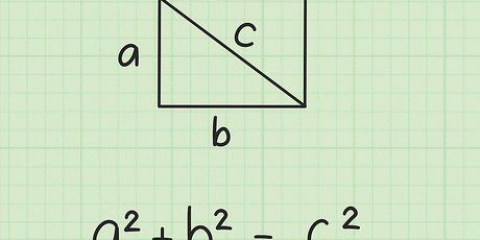
1. Lær Pythagoras` sætning. Pythagoras sætning beskriver forholdet mellem siderne i en retvinklet trekant. Den siger, at for en vilkårlig retvinklet trekant med siderne a og b og hypotenusen af længden c, har vi a + b = c.

2. Sørg for, at din trekant er en retvinklet trekant.Pythagoras sætning virker kun for retvinklede trekanter, og per definition kan kun en retvinklet trekant have en hypotenus.Hvis din trekant indeholder en vinkel på præcis 90 grader, så er det en retvinklet trekant, og du kan fortsætte.

3. Tildel variablerne a, b og c til siderne af din trekant.Variablen "c" er altid tildelt hypotenusen, altså den længste side.Vælg en af de andre sider til -en, og navngiv den resterende side b (det er lige meget hvilken, matematikken forbliver den samme).Bearbejd derefter længderne af a og b til formlen, som vist i følgende eksempel:

4. Bestem kvadraterne af a og b.For at finde kvadratet af et tal skal du bare gange det tal med sig selv, så a = a x a. Find kvadraterne af både a og b, og inkorporer dem i formlen.

5. Tæl værdierne af-en og b sammen på. Tag dette ind i din ligning, og det giver dig værdien af c. Nu er der kun et skridt tilbage, og du har bestemt hypotenusen!

6. Bestem kvadratroden af c. Brug kvadratrodsfunktionen på din lommeregner (eller multiplikationstabeller, hvis du kender dem udenad) til at finde kvadratroden af c. Svaret er længden af din hypotenusa!
Metode 2 af 3: Bestemmelse af hypotenusen af specielle retvinklede trekanter

1. Lær at genkende trekanter i en pythagoras trekant. Længderne af siderne af en pythagoras triade er heltal, der adlyder Pythagoras sætning. Du vil jævnligt støde på disse specielle trekanter i geometrilærebøger og i standardtests såsom SAT og GRE.Især, hvis du husker de første 2 Pythagoras tripler, kan du spare dig selv for en masse tid på disse tests, fordi du med det samme kender hypotenusen af en af disse trekanter bare ved at se på længderne af siderne!
- Den første pythagoras trio er 3-4-5 (3 + 4 = 5, 9 + 16 = 25).Når du ser en retvinklet trekant med sider af længden 3 og 4, ved du med det samme med sikkerhed, at hypotenusen bliver 5 uden at skulle lave nogen beregninger.
- Forholdet mellem en pythagoras trippel forbliver den samme, selv når siderne ganges med et andet tal. For eksempel: en retvinklet trekant med sider 6 og 8 vil have en hypotenus på 10 (6 + 8 = 10, 36 + 64 = 100).Det samme gælder for9-12-15, også selvom 1,5-2-2,5.Gør beregningerne, og du vil se!
- Den anden pythagoras trio, som du ofte vil støde på i tests er 5-12-13 (5 + 12 = 13, 25 + 144 = 169).Pas også på dens flertalsformer, som f.eks 10-24-26 og 2,5-6-6,5.

2. Lær forholdet mellem siderne i en retvinklet trekant med vinklerne 45-45-90. En 45-45-90 retvinklet trekant har vinkler på 45, 45 og 90 grader, og kaldes også en ligebenet retvinklet trekant. Denne findes ofte i standardtests og er en meget nem trekant at løse. Forholdet mellem siderne i denne trekant er 1:1:Sqrt(2), hvilket betyder, at længden af benene er ens, og længden af hypotenusen er så blot længden af benene ganget med kvadratroden af to.

3. Lær proportionerne af en retvinklet 30-60-90 trekant. Denne trekant har vinkler på 30, 60 og 90 grader og kan laves ved at dele en ligesidet trekant i to. Siderne i den retvinklede trekant 30-60-90 har altid forholdet 1:Sqrt(3):2, eller x:Sqrt(3)x:2x.Hvis man får længden af det ene ben i den højre 30-60-90 trekant og bliver bedt om at bestemme hypotenusen, er det meget nemt at gøre:
Metode 3 af 3: Beregning af hypotenusen med sinusreglen

1. Forstå hvad "Bihule" midler. Vilkårene "bihule," "cosinus" og "tangent" alle refererer til bestemte proportioner mellem vinklerne og/eller siderne i en retvinklet trekant.I en retvinklet trekant er er bihule af en vinkel defineret som længden af siden modsat vinklen divideret med trekantens hypotenus. Forkortelsen for sinus, som den står på din lommeregner er synd.

2. Lær hvordan du beregner sinus. Selv en simpel videnskabelig lommeregner har en sinusfunktion. Se på nøglen markeret synd.For at finde sinus af en vinkel vil du normalt trykke på synd-tast og indtast derefter vinklen i grader.På nogle lommeregnere skal du dog først indtaste vinklen i grader og derefter trykke på synd-tryk på knappen. Du bliver nødt til at eksperimentere med din lommeregner eller se i manualen for at finde ud af, hvilken det er.

3. Lær sinusreglen.Sinusreglen er et nyttigt værktøj til at løse trekantsproblemer. Du kan hovedsageligt bruge det til at finde hypotenusen af en retvinklet trekant, hvis du kender længden af den ene side og en af dens vinkler ud over den rette vinkel. Til enhver trekant med sider -en, b og c og hjørnerne -en, B og C, sinusreglen siger det en / synd -en = b / synd B = c / synd C.

4. Tildel variablerne a, b og c til siderne af din trekant. Hypotenusen (den længste side) skal altid være "c" er. For nemheds skyld skal du mærke siden med kendt længde som "-en" og andre "b". Tildel derefter variablerne A, B og C til trekantens hjørner. Den rette vinkel modsat hypotenusen bliver så "C".Hjørnet overfor "-en" er vinkel "-en" og vinklen modsatte side "b" er "B".

5. Beregn den tredje vinkel. Fordi det er en ret vinkel, ved du det allerede C = 90 grader og du ved også hvilken vinkel -en eller B er. Da summen af alle vinkler i en trekant altid skal være lig 180 grader, er det let at beregne den tredje vinkel ved hjælp af formlen: 180 – (90 + A) = B. Du kan også vende denne ligning så 180 – (90 + B) = A.

6. Undersøg din trekant.På dette tidspunkt kender du alle trekantens vinkler og længden af side a. Nu er det tid til at bearbejde disse værdier til sinusreglen for at beregne længden af de to andre sider.

7. Anvend sinusreglen på din trekant.Vi skal blot behandle vores tal og løse følgende ligning for at finde længden af hypotenusen c: længde af side a / synd A = længden af siden c / synd C.Dette kan stadig se lidt skræmmende ud, men 90 graders sinus er en konstant og er altid lig med 1!Vores ligning kan derfor forenkles til: en / synd A = c/1, eller enklere en / synd A = c.

8. Fordel længden af silke-en gennem vinklens sinus -en at finde længden af hypotenusen!Du kan beregne dette i to separate trin ved først at: synd Beregn og skriv A, divider derefter med a. Eller test det hele på én gang i din lommeregner. Hvis du gør dette, så glem ikke parentesen efter divisionstegnet.Indtast f.eks 10/(synd 40) eller 10 / (40 synd), afhængig af din lommeregner.
Artikler om emnet "Bestemmelse af længden af hypotenusen"
Оцените, пожалуйста статью
Lignende
Populær