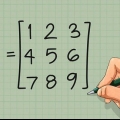Bestemmelse af determinanten for en 3x3 matrix: 12 trin (med billeder)

Indhold

Trin
- Del 1 af 2: Bestemmelse af determinanten
- Del 2 af 2: Forenkling af problemet
Tips

Determinanten af en matrix er meget brugt i matematik, lineær algebra og højere geometri. Uden for den videnskabelige verden bruger computergrafikingeniører og programmører ofte determinanterne for matricer. Læs denne artikel for at bestemme determinanten for en 3x3 matrix.

Trin

Del 1 af 2: Bestemmelse af determinanten

1. Skriv din 3 x 3 matrix ned. Vi starter med en 3 x 3 matrix A og prøver determinanten |A| at kunne lide det. Vi bruger følgende generelle notation for matricen (og dette er vores eksempelmatrix):

$m = (\begin{matrix} -en \end{matrix} 11 {-en}_{12} {-en}_{13} {-en}_{21} & {-en}_{22} & {-en}_{23} {-en}_{31} & {-en}_{32} & {-en}_{33}) = (\begin{matrix} 1 & 5 & 3 \\ 2 & 4 & 7 \\ 4 & 6 & 2 \end{matrix})$ $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{ {23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2& 4&7\4&6&2end{pmatrix}}$

Billede med titlen Find determinanten for en 3X3-matrix Trin 2

2. Vælg en række eller kolonne. Dette vil være din referencerække eller kolonne. Du får det samme svar, uanset hvilken du vælger. Vælg nu bare den første række. Senere vil vi rådgive dig om, hvordan du vælger den mulighed, der er lettest at beregne.

Lad os vælge den første række i vores eksempelmatrix A. Sæt en ring om 1 5 3. Sæt generelt en cirkel om a₁₁ -en₁₂ -en₁₃.

Billede med titlen Find determinanten for en 3X3-matrix Trin 3

3. Kryds rækken og kolonnen af det første element ud. Se på rækken eller kolonnen, du har sat en cirkel med, og vælg det første element. Tegn en linje gennem den tilsvarende række og kolonne. Hvis alt går vel, giver dette nu fire tal. Vi behandler dette som en 2 x 2 matrix.

I vores eksempel er referencerækken 1 5 3. Det første element er i række 1 og kolonne 1. Overstrege række 1 og kolonne 1 helt. Skriv de resterende elementer ned som en2 x 2 matrix:

~~1 5 3~~
2 4 7
4 6 2

Billede med titlen Find determinanten for en 3X3-matrix Trin 4

4. Bestem determinanten for 2 x 2 matrixen. Glem ikke: matrixen

(\begin{matrix} -en & b \\ c & d \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ har en determinant af ad - f.Kr. Det ved du ved at tegne et kryds (X) gennem 2 x 2 matrixen. Multiplicer de to tal forbundet med af X. Træk derefter produktet af de to tal, der er forbundet med /. Brug denne formel til at beregne determinanten for den matrix, du lige har fundet.

I vores eksempel er determinanten for matricen

(\begin{matrix} 4 & 7 \\ 6 & 2 \end{matrix})

${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34.

Denne determinant kaldes mindre af det element, vi valgte i vores originale matrix. I dette tilfælde har vi den mindreårige af -en₁₁ fundet det.

Billede med titlen Find determinanten for en 3X3-matrix Trin 5

5. Gang svaret med dit valgte element. Husk, at du valgte et element fra din referencerække (eller kolonne), da du besluttede, hvilken række og kolonne der skulle streges ud. Multiplicer dette element med den determinant, du lige har beregnet for 2x2-matricen.

I vores eksempel har vi en₁₁ valgt, som har en værdi på 1. Multiplicer dette med -34 (determinanten for 2x2-matricen) for at få 1*-34 = -34 at få.

Billede med titlen Find determinanten for en 3X3-matrix Trin 6

6. Bestem tegnet på dit svar. Gang nu svaret med 1 eller med -1 for at få cofaktor af dit valgte element. Hvilken du bruger afhænger af elementets placering i 3x3-matricen. Husk følgende enkle tabel for at finde ud af, hvilket element der forårsager hvad:

+ - +
- + -
+ - +

Fordi vi -en₁₁ har valgt, markeret med et +, gange vi tallet med +1 (med andre ord, vi gør ikke noget ved det). Svaret er stadig -34.

En anden måde at bestemme tegnet på er med formlen (-1), hvor jeg og j danner rækken og kolonnen af elementet.

Billede med titlen Find determinanten for en 3X3-matrix Trin 7

7. Gentag denne proces for det andet element i din referencerække eller kolonne. Fortsæt med den originale 3x3 matrix, med rækken eller kolonnen, som du cirklede med tidligere. Gentag den samme proces med dette element:

Kryds rækken og kolonnen for det element. I dette tilfælde vælger du elementet a₁₂ (med værdi 5). Kryds den første række (1 5 3) og den anden kolonne

(\begin{matrix} 5 \\ 4 \\ 6 \end{matrix})

${begin{pmatrix}5\4\6end{pmatrix}}$ .

Behandl de resterende elementer som en 2x2 matrix. I vores eksempel er matricen

(\begin{matrix} 2 & 7 \\ 4 & 2 \end{matrix})

${begin{pmatrix}2&7\4&2end{pmatrix}}$

Bestem determinanten for denne 2x2 matrix. Brug formlen ad - bc. (2*2 - 7*4 = -24)

Multiplicer dette med det valgte element i 3x3-matricen. -24 * 5 = -120

Bestem, om der skal ganges med -1. Brug tegntabellen eller formlen (-1). Vi har element a₁₂ valgt, og det er en – på karaktertabellen. Vi skal ændre tegnet for vores svar: (-1)*(-120) = 120.

Billede med titlen Find determinanten for en 3X3-matrix Trin 8

8. Gentag for det tredje element. Du skal nu finde en co-faktor. Beregn i for det tredje led i din referencerække eller kolonne. Her er en hurtig forklaring på, hvordan man beregner cofaktoren for ₁₃ i vores eksempel:

Kryds række 1 og kolonne 3 og få

(\begin{matrix} 2 & 4 \\ 4 & 6 \end{matrix})

${begin{pmatrix}2&4\4&6end{pmatrix}}$

Dens determinant er 2*6 - 4*4 = -4.

Gang dette med elementet a₁₃: -4 * 3 = -12.

element a₁₃ er et + på tegntabellen, så svaret er -12.

Billede med titlen Find determinanten for en 3X3-matrix Trin 9

9. Læg de tre resultater sammen. Dette er det sidste skridt. Du har beregnet cofaktorer, en for hvert element i en enkelt række eller kolonne. Tilføj disse sammen, og du har fundet determinanten for 3x3-matricen.

I vores eksempel er determinanten -34 + 120 + -12 = 74.

Del 2 af 2: Forenkling af problemet

Billede med titlen Find determinanten for en 3X3-matrix Trin 10

1. Vælg referencen med flest nuller. Glem ikke, at du hver kan vælge række eller kolonne som reference. Du får det samme svar, uanset hvad du vælger. Hvis du vælger en række eller kolonne med nuller, skal du kun beregne cofaktoren for de elementer, der ikke er nul. Årsagen er som følger:

Antag, at du vælger række 2 med elementerne a₂₁, -en₂₂, og en₂₃. For at løse dette problem ser vi på tre forskellige 2x2-matricer. Antag, at vi kalder dette A₂₁, -en₂₂ og A₂₃.
Determinanten for 3x3 matrixen er en₂₁|A₂₁| - en₂₂|A₂₂| + a₂₃|A₂₃|.
Hvis vilkårene a₂₂ og en₂₃ er begge 0, så bliver vores formel₂₁|A₂₁| - 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| - 0 + 0 = a₂₁|A₂₁|. Nu mangler vi bare at beregne cofaktoren for et enkelt element.

Billede med titlen Find determinanten for en 3X3-matrix Trin 11

2. Tilføj rækkerne sammen for at forenkle matrixen. Hvis du tager værdierne af en række og tilføjer dem til en anden række, ændres matricens determinant ikke. Det samme gælder for kolonner. Du kan gøre dette gentagne gange - eller gange værdierne med en konstant, før du tilføjer - for at få så mange nuller i matrixen som muligt. Dette kan spare dig for meget arbejde.

Antag for eksempel, at du har en 3x3 matrix:

(\begin{matrix} 9 & - 1 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}9&-1&2\3&1&0\7&5&-2end{pmatrix}}$

Hver 9. i position a₁₁ for at slippe af med det, kan vi gange den anden række med -3 og lægge resultatet til den første. Den nye første række bliver så [9 -1 2] + [-9 -3 0] = [0 -4 2].

Den nye matrix er

(\begin{matrix} 0 & - 4 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}0&-4&2\3&1&0\7&5&-2end{pmatrix}}$ Prøv at bruge det samme trick til kolonnerne, for at₁₂ at lave en 0.

Billede med titlen Find determinanten for en 3X3-matrix Trin 12

3. Lær tricket til at løse trekantmatricer. I disse specielle tilfælde er determinanten blot produktet af elementerne langs hoveddiagonalen fra a₁₁ øverst til venstre til a₃₃ nederst til højre. Vi taler stadig om 3x3 matricer, men `trekantede` matricer har specielle værdimønstre, der ikke nul er:

Øvre trekantsmatrix: Alle elementer, der ikke er nul, er på eller over hoveddiagonalen. Alle værdier nedenfor er nul.

Nedre trekantsmatrix: Alle elementer, der ikke er nul, er på eller under hoveddiagonalen.

Diagonal matrix: Alle ikke-nul elementer er på hoveddiagonalen. (En delmængde af ovenstående.)

Tips

Denne metode kan bruges til kvadratiske matricer af enhver størrelse. For eksempel, hvis du bruger dette til en 4x4 matrix, så holder du efter "strege over" en 3x3 matrix, som du kan beregne determinanten for som angivet ovenfor. Vær advaret, for at gøre dette i hånden vil være meget kedeligt!
Hvis alle elementer i en række eller kolonne er lig med 0, så er determinanten af denne matrix lig med 0.