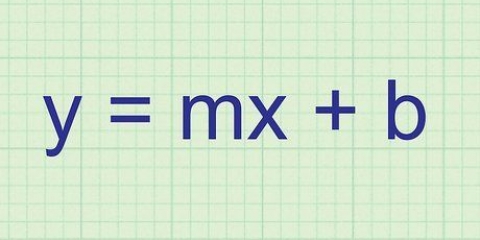Bestemmelse af korrelationskoefficienten

Indhold

Trin
Tips
Advarsler

Korrelationskoefficienten, betegnet som r eller ρ, er målet for den lineære korrelation (forholdet, både i styrke og retning) mellem to variable. Det spænder fra -1 til +1 ved at bruge plus- og minustegn til at repræsentere den positive og negative korrelation. Hvis korrelationskoefficienten er præcis -1, så er forholdet mellem de to variable fuldstændig negativt; hvis korrelationskoefficienten er præcis +1, så er sammenhængen fuldstændig positiv. To variable kan have en positiv korrelation, en negativ korrelation eller slet ingen korrelation. Du kan beregne korrelationen i hånden ved at bruge nogle gratis korrelationsberegnere, der er tilgængelige online, eller ved at bruge de statistiske funktioner i en god grafregner.

Trin

Metode 1 af 4: Beregning af korrelationskoefficienten i hånden

1. Indsaml dine data først. For at begynde at beregne en effektiv korrelation skal du først undersøge dataparrene. Det er nyttigt at sætte dem i et bord, både lodret og vandret. Mærk hver række eller kolonne x og y.

For eksempel: Antag, at du har fire datapar til x og y. Tabellen kunne så se sådan ud:

x || y
1 || 1
2 || 3
4 || 5
5 || 7

Billede med titlen Find korrelationskoefficienten Trin 2

2. Beregn middelværdien af x. For at beregne middelværdien skal du tilføje alle værdierne af x add og divider derefter med antallet af værdier.

Med udgangspunkt i ovenstående eksempel skal du bemærke, at du har fire værdier for x. For at beregne gennemsnittet, tæl alle værdier for x og dividere det med 4. Regnestykket ser så således ud:

μ x = (1 + 2 + 4 + 5) / 4

${displaystyle mu _{x}=(1+2+4+5)/4}$

μ x = 12 / 4

${displaystyle mu _{x}=12/4}$

μ x = 3

${displaystyle mu _{x}=3}$

Billede med titlen Find korrelationskoefficienten Trin 3

3. Find middelværdien af y. For at få gennemsnittet af y For at finde det skal du følge de samme trin, lægge alle værdierne af y sammen og derefter dividere med antallet af værdier.

I eksemplet ovenfor har du også fire værdier for y. Læg alle disse værdier sammen og divider derefter med 4. Beregningerne vil så se således ud:

μ y = (1 + 3 + 5 + 7) / 4

${displaystyle mu _{y}=(1+3+5+7)/4}$

μ y = 16 / 4

${displaystyle mu _{y}=16/4}$

μ y = 4

${displaystyle mu _{y}=4}$

Billede med titlen Find korrelationskoefficienten Trin 4

4. Bestem standardafvigelsen for x. Når du har dine midler, kan du beregne standardafvigelsen. Brug formlen til dette:

Σ x = \sqrt{} 1 n - 1 Σ (x - μ_{x})^{2}

${displaystyle sigma _{x}={sqrt {{frac {1}{n-1}}Sigma (x-mu _{x})^{2}}}}$

Med prøvedataene vil dine beregninger se sådan ud:

Σ x = \sqrt{} 1 4 - 1 * ((1 - 3)^{2} + (2 - 3)^{2} + (4 - 3)^{2} + (5 - 3)^{2})

${displaystyle sigma _{x}={sqrt {{frac {1}{4-1}}*((1-3)^{2}+(2-3)^{2}+(4 -3)^{2}+(5-3)^{2})}}}$

Σ x = \sqrt{} \frac{1}{3} * (4 + 1 + 1 + 4)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(4+1+1+4)}}}$

Σ x = \sqrt{} \frac{1}{3} * (10)

${displaystyle sigma _{x}={sqrt {{frac {1}{3}}*(10)}}}$

Σ x = \sqrt{\frac{10}{3}}

${displaystyle sigma _{x}={sqrt {frac {10}{3}}}}$

Σ x = 1, 83

${displaystyle sigma _{x}=1,83}$

Billede med titlen Find korrelationskoefficienten Trin 5

5. Beregn standardafvigelsen for y. Brug de samme grundlæggende trin til at finde standardafvigelsen for y. Du vil bruge den samme formel ved at bruge datapunkterne for y.

Med prøvedataene vil dine beregninger se sådan ud:

Σ y = \sqrt{} 1 4 - 1 * ((1 - 4)^{2} + (3 - 4)^{2} + (5 - 4)^{2} + (7 - 4)^{2})

${displaystyle sigma _{y}={sqrt {{frac {1}{4-1}}*((1-4)^{2}+(3-4)^{2}+(5 -4)^{2}+(7-4)^{2})}}}$

Σ y = \sqrt{} \frac{1}{3} * (9 + 1 + 1 + 9)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(9+1+1+9)}}}$

Σ y = \sqrt{} \frac{1}{3} * (20)

${displaystyle sigma _{y}={sqrt {{frac {1}{3}}*(20)}}}$

Σ y = \sqrt{\frac{20}{3}}

${displaystyle sigma _{y}={sqrt {frac {20}{3}}}}$

Σ y = 2, 58

${displaystyle sigma _{y}=2,58}$

Billede med titlen Find korrelationskoefficienten Trin 6

6. Se den grundlæggende formel til bestemmelse af en korrelationskoefficient. Formlen til beregning af en korrelationskoefficient bruger middelværdier, standardafvigelser og antallet af par i et datasæt (repræsenteret ved n). Selve korrelationskoefficienten er repræsenteret af det lille bogstav r eller det græske bogstav ρ (rho). Til denne artikel vil vi bruge formlen kendt som Pearson-korrelationskoefficienten som vist nedenfor:

ρ = (1 n - 1) Σ (x - μ x Σ_{x}) * (y - μ y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

Du vil muligvis bemærke små variationer i formlen, her eller i andre forklaringer. For eksempel vil nogle bruge den græske notation med rho og sigma, mens andre vil bruge r og s. Nogle forklaringer kan bruge lidt forskellige formler, men de vil matematisk svare til denne.

Billede med titlen Find korrelationskoefficienten Trin 7

7. Bestem korrelationskoefficienten. Du har nu midlerne og standardafvigelserne for dine variabler, så du kan gå videre til korrelationskoefficientformlen. Huske på, at n repræsenterer antallet af værdier, du har. Du har allerede udarbejdet de andre relevante oplysninger i ovenstående trin.

Ved at bruge prøvedataene kan du indtaste dataene i korrelationskoefficientformlen og beregne det sådan:

ρ = (1 n - 1) Σ (x - μ x Σ_{x}) * (y - μ y Σ_{y})

${displaystyle rho =left({frac {1}{n-1}}right)Sigma left({frac {x-mu _{x}}{sigma _{x}} }right)*left({frac {y-mu _{y}}{sigma _{y}}}right)}$

ρ = (\frac{1}{3}) *

${displaystyle rho =left({frac {1}{3}}right)*}$ [

(1 - 3 1, 83) * (1 - 4 2, 58) + (2 - 3 1, 83) * (3 - 4 2, 58)

${displaystyle left({frac {1-3}{1.83}}right)*left({frac {1-4}{2.58}}right)+left({frac {2- 3}{1.83}}right)*left({frac {3-4}{2.58}}right)}$

+ (4 - 3 1, 83) * (5 - 4 2, 58) + (5 - 3 1, 83) * (7 - 4 2, 58)

${displaystyle +left({frac {4-3}{1.83}}right)*left({frac {5-4}{2.58}}right)+left({ frac {5 -3}{1.83}}right)*left({frac {7-4}{2.58}}right)}$ ]

ρ = (\frac{1}{3}) * (6 + 1 + 1 + 6 4, 721)

${displaystyle rho =left({frac {1}{3}}right)*left({frac {6+1+1+6}{4.721}}right)}$

ρ = (\frac{1}{3}) * 2, 965

${displaystyle rho =left({frac {1}{3}}right)*2.965}$

ρ = (2, 965 3)

${displaystyle rho =left({frac {2.965}{3}}right)}$

ρ = 0, 988

${displaystyle rho =0,988}$

Billede med titlen Find korrelationskoefficienten Trin 8

8. Fortolk resultatet. For dette datasæt er korrelationskoefficienten 0,988. Dette tal fortæller dig to ting om dataene. Se på tallets tegn og tallets størrelse.

Da korrelationskoefficienten er positiv, kan man sige, at der er en positiv sammenhæng mellem x-data og y-data. Det betyder, at når x-værdierne stiger, forventer du, at y-værdierne også stiger.

Da korrelationskoefficienten er meget tæt på +1, er x-data og y-data meget tæt forbundne. Hvis du skulle tegne disse punkter, ville du se, at de er en meget god tilnærmelse af en ret linje.

Metode 2 af 4: Brug af online korrelationsberegnere

Billede med titlen Find korrelationskoefficienten Trin 9

1. Søg online efter korrelationsberegnere. At måle korrelation er en ret standard beregning for statistikere. Beregningen kan blive meget kedelig for store datasæt, hvis den udføres i hånden. Derfor har mange kilder gjort almindelige korrelationsberegninger tilgængelige online. Brug en hvilken som helst søgemaskine og indtast søgeordet `korrelationsberegner`.

Billede med titlen Find korrelationskoefficienten Trin 10

2. For data i. Læs venligst instruktionerne på hjemmesiden omhyggeligt, så du kan indtaste dataene korrekt. Det er vigtigt, at datapar holdes i orden, ellers får du et forkert korrelationsresultat. Forskellige websteder bruger forskellig formatering til at indtaste data.

For eksempel: på hjemmesiden http://ncalculators.com/statistics/correlation-coefficient-calculator.htm find en vandret boks til at indtaste x-værdier og en anden vandret boks til at indtaste y-værdier. Du indtaster kun vilkårene adskilt af kommaer. Så x-datasættet beregnet tidligere i denne artikel skal indtastes som 1,2,4,5. Y-datasættet indtastes som 1,3,5,7.

På en anden side, http://www.alkohol.com/calculators/statistics/correlation-coefficient/, du kan indtaste data både vandret og lodret, så længe du holder datapunkterne i orden.

Billede med titlen Find korrelationskoefficienten Trin 11

3. Beregn resultaterne. Disse beregningssider er populære, fordi alt hvad du skal gøre efter at have indtastet data generelt er at klikke på knappen `Beregn` -- resultatet vises automatisk.

Metode 3 af 4: Brug af en grafregner

Billede med titlen Find korrelationskoefficienten Trin 12

1. Indtast dine oplysninger. Slå statistikfunktionen til på din grafregner og vælg derefter kommandoen `Rediger`.

Hver lommeregner har lidt forskellige tastekommandoer. Denne artikel indeholder specifikke instruktioner til Texas Instruments TI-86.
Gå ind i Stat-funktionen ved at trykke på [2nd]-Stat (over `+`-tasten) og derefter F2-Edit.

Billede med titlen Find korrelationskoefficienten Trin 13

2. Ryd alle gamle gemte data. De fleste lommeregnere gemmer de statistiske data, indtil de er ryddet. For at sikre dig, at du ikke forveksler gamle data med nye data, skal du først rydde alle tidligere gemte oplysninger.

Brug piletasterne til at flytte markøren for at fremhæve kategorien `xStat`. Tryk derefter på `Slet` og `Enter. Dette bør rydde alle værdier i xStat-kolonnen.

Brug piletasterne til at fremhæve kategorien `yStat`. Tryk på `Slet` og `Enter` for også at rydde dataene fra den kolonne.

Billede med titlen Find korrelationskoefficienten Trin 14

3. Indtast dine dataværdier. Brug piletasterne til at flytte markøren til det første mellemrum under xStat-overskriften. Indtast din første dataværdi, og tryk derefter på Enter. Du bør se pladsen nederst på skærmen `xStat(1)=__`, hvor din værdi udfylder den tomme plads. Når du trykker på Enter, vil data udfylde tabellen, markøren vil flytte til næste linje, og linjen nederst på skærmen skulle nu læse `xStat(2)=__`.

Fortsæt med at indtaste alle x-værdier.

Når du har indtastet x-værdierne, skal du bruge piletasterne til at flytte til kolonnen yStat og indtaste y-værdierne.

Når alle data er indtastet, skal du trykke på Exit for at rydde skærmen og afslutte Stat-menuen.

Billede med titlen Find korrelationskoefficienten Trin 15

4. Beregn den lineære regressionsstatistik. Korrelationskoefficienten er et mål for, hvor godt dataene nærmer sig en ret linje. En grafregner med statistiske funktioner kan meget hurtigt beregne den bedst tilpassede linje og korrelationskoefficient.

Gå ind i Stat-funktionen, og tryk derefter på Calc-knappen. På TI-86 er dette [2nd][Stat][F1].

Vælg de lineære regressionsberegninger. På TI-86 er den [F3], mærket "LinR.` Den grafiske skærm vil så vise linjen `LinR _` med en blinkende markør.

Du skal nu indtaste navnene på de to variable, du vil beregne. Disse er xStat og yStat.

På TI-86 skal du vælge listen over navne (`Names`) ved at trykke på [2nd][List][F3].

Den nederste linje på din skærm skulle nu vise de tilgængelige variabler. Vælg [xStat] (dette er sandsynligvis knap F1 eller F2), indtast derefter et komma og derefter [yStat].

Tryk på Enter for at beregne dataene

Billede med titlen Find korrelationskoefficienten Trin 16

5. Fortolk resultaterne. Når du trykker på Enter, beregner lommeregneren straks følgende information for de indtastede data:

y = -en + b x

${displaystyle y=a+bx}$ : Dette er den generelle formel for en ret linje. Men i stedet for det velkendte `y=mx+b` præsenteres dette i omvendt rækkefølge.

-en =

${displaystyle a=}$ . Dette er værdien af skæringspunktet med y-aksen på den linje, der passer bedst.

b =

${displaystyle b=}$ . Dette er den hældning af linjen, der passer bedst.

korrekt =

${displaystyle {text{corr}}=}$ . Dette er korrelationskoefficienten.

n =

${displaystyle n=}$ . Dette er antallet af datapar brugt i beregningen.

Metode 4 af 4: Gentagelse af det grundlæggende

Billede med titlen Find korrelationskoefficienten Trin 17

1. Forstå begrebet korrelation. Korrelation refererer til det statistiske forhold mellem to størrelser. Korrelationskoefficienten er et enkelt tal, som du kan beregne for to sæt datapunkter. Tallet er altid noget mellem -1 og +1 og angiver, hvor tæt de to datasæt er forbundet.

For eksempel, hvis du målte højden og alderen på børn op til omkring 12 år, ville du forvente at finde en stærk positiv sammenhæng. Når børn bliver ældre, har de en tendens til at blive højere.
Et eksempel på en negativ sammenhæng er at sammenligne den tid, nogen bruger på at øve golf, og denne persons golfscore. Efterhånden som træningen skrider frem, bør scoren falde.
I sidste ende ville du forvente ringe sammenhæng, positiv eller negativ, mellem f.eks. en persons skostørrelse og deres eksamenskarakterer.

Billede med titlen Find korrelationskoefficienten Trin 18

2. Beregn gennemsnittet. Det aritmetiske middel eller "middelværdi" af et sæt data beregnes ved at lægge alle værdierne af data sammen og derefter dividere med antallet af værdier i sættet. Når du vil bestemme korrelationskoefficienten for dine data, skal du beregne gennemsnittet af hvert sæt data.

Middelværdien af en variabel er angivet ved variablen med en vandret linje over den. Dette omtales ofte som `x-bar` eller `y-bar` for datasættene af x og y. Alternativt kan middelværdien angives med det lille græske bogstav μ (mu). For eksempel, for at repræsentere middelværdien af datapunkter for x, kan du bruge μ_x eller μ(x).

For eksempel, hvis du har et sæt af x (1,2,5,6,9,10), så vil gennemsnittet af disse data blive beregnet som følger:

μ x = (1 + 2 + 5 + 6 + 9 + 10) / 6

${displaystyle mu _{x}=(1+2+5+6+9+10)/6}$

μ x = 33 / 6

${displaystyle mu _{x}=33/6}$

μ x = 5, 5

${displaystyle mu _{x}=5,5}$

Billede med titlen Find korrelationskoefficienten Trin 19

3. Kend vigtigheden af standardafvigelsen. I statistik måler standardafvigelsen variation, der viser spredningen af tallene i forhold til gennemsnittet. En gruppe af tal med en lav standardafvigelse er ret tæt på hinanden. En gruppe af tal med en høj standardafvigelse er mere spredt.

Som et symbol er standardafvigelsen udtrykt med det lille bogstav s eller det græske bogstav σ (sigma). Så standardafvigelsen for x-dataene skrives som s_x eller_x.

Billede med titlen Find korrelationskoefficienten Trin 20

4. Genkend summeringsnotationen. Summeringsoperatoren er en af de mest almindelige operatorer i matematik, der repræsenterer en sum af værdier. Det er repræsenteret med det græske store bogstav, sigma eller ∑.

For eksempel, hvis du har et sæt datapunkter x (1,2,5,6,9,10), betyder ∑x:

1+2+5+6+9+10 = 33

Tips

Korrelationskoefficienten omtales nogle gange som `Pearson produkt-moment korrelationskoefficient` til ære for Karl Pearson, dens udvikler.
Generelt repræsenterer en korrelationskoefficient større end 0,8 (positiv eller negativ) en stærk korrelation; en korrelationskoefficient lavere end 0,5 (igen positiv eller negativ) repræsenterer en svag korrelationskoefficient.

Advarsler

Korrelation viser, at to sæt data på en eller anden måde er forbundet. Pas dog på ikke at tolke dette som en årsagssammenhæng. For eksempel, hvis du sammenligner folks skostørrelser og deres højde, vil du sandsynligvis finde en stærk positiv sammenhæng. Større mennesker har generelt større fødder. Det betyder dog ikke, at det at blive høj vil få dine fødder til at vokse, eller at store fødder vil gøre dig høj. De sker bare sammen.