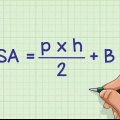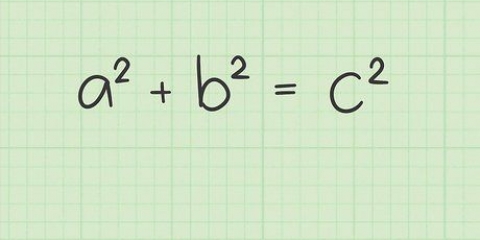For eksempel, hvis du vil finde bredden af et rektangel med et areal på 24 cm og en længde på 8 cm, vil din formel se sådan ud:


For eksempel i ligningen  , divider hver side med 8.
, divider hver side med 8.




For eksempel for et rektangel med et areal på  og en længde på
og en længde på  , bliver til bredden
, bliver til bredden  .
. 
Hvis du for eksempel ville finde bredden af et rektangel med en omkreds på 22 cm og en længde på 8 cm, ville formlen se sådan ud:



For eksempel i ligningen  , træk 16 fra hver side, og divider med 2.
, træk 16 fra hver side, og divider med 2.





For eksempel for et rektangel med en omkreds på  og en længde på
og en længde på  , bliver til bredden
, bliver til bredden  .
. 

For eksempel, når du bestemmer bredden af et rektangel med en diagonal på 5 cm og en side på 4 cm, vil formlen se sådan ud: 

For eksempel:




For eksempel i ligningen  , trække 16 fra hver side.
, trække 16 fra hver side.



For eksempel:



For eksempel for et rektangel med en diagonal på  og den ene side af
og den ene side af  , bliver til bredden
, bliver til bredden  .
. 

Sammenhængen kan gives ved at angive, hvor mange gange den ene side er større end den anden, eller hvor mange enheder mere eller mindre. For eksempel kan det vides, at længden er fem centimeter længere end bredden. Udtrykket for længden bliver så  .
. 
For eksempel hvis du ved, at arealet er 24 cm, og det  , så ser formlen sådan ud:
, så ser formlen sådan ud:



Forenkle f.eks  så længe
så længe  .
. 
Du skal muligvis tilføje eller trække fra for at løse dette, eller faktor eller bruge en andengradsligning til at løse dette. For eksempel,  kan opløses som følger:
kan opløses som følger:


Du har så to mulige løsninger på :
: eller
eller  . Da et rektangel ikke kan have en negativ bredde, kan du udelukke -8. Det er din løsning også
. Da et rektangel ikke kan have en negativ bredde, kan du udelukke -8. Det er din løsning også  .
.
Bestemmelse af bredden af et rektangel
Indhold
Der er utallige måder at finde de manglende dimensioner af et rektangel, og den metode du bruger vil afhænge af de data du har. Så længe arealet eller omkredsen er kendt, såvel som længden af den ene side af rektanglet (eller forholdet mellem længden og bredden), kan den manglende dimension bestemmes. Egenskaberne for et rektangel er sådan, at disse metoder kan bruges til at bestemme dets bredde- eller længdegrad.
Trin
Metode 1 af 4: Brug af arealet og længden

1. Skriv ned formlen for arealet af et rektangel. Formlen er  , hvorved
, hvorved  er lig med arealet af rektanglet,
er lig med arealet af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde.
 , hvorved
, hvorved  er lig med arealet af rektanglet,
er lig med arealet af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde. - Metoden virker kun for et givet areal og længde af rektanglet.
- Denne formel er også tilgængelig i formularen
, hvorved
er lig med højden af rektanglet (i stedet for længden). Disse to udtryk refererer til de samme dimensioner.

2. Brug areal- og længdeværdierne i formlen. Sørg for at erstatte de korrekte variabler.


3. Løs for w  . Det gør du ved at dividere hver side af ligningen med dens længde.
. Det gør du ved at dividere hver side af ligningen med dens længde.
 . Det gør du ved at dividere hver side af ligningen med dens længde.
. Det gør du ved at dividere hver side af ligningen med dens længde. , divider hver side med 8.
, divider hver side med 8.



4. Skriv dit endelige svar ned. Glem ikke at nævne enheden for aflæsningerne.
 og en længde på
og en længde på  , bliver til bredden
, bliver til bredden  .
.Metode 2 af 4: Brug af omkreds og længde
1. Skriv formlen for omkredsen af et rektangel. Formlen er  , hvorved
, hvorved  er lig med omkredsen af rektanglet,
er lig med omkredsen af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde.
 , hvorved
, hvorved  er lig med omkredsen af rektanglet,
er lig med omkredsen af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde.- Denne metode virker kun for en given omkreds og længde af rektanglet.
- Denne formel er også skrevet som
, hvorved
er lig med højden af rektanglet og bruges i stedet for længden. Variablerne
og
refererer til de samme dimensioner, og den fordelende egenskab dikterer, at disse to formler, selvom de er ordnet forskelligt, giver det samme resultat.

2. Brug omkreds og længde i formlen. Sørg for at erstatte de korrekte variabler.



3. Løse w  . For at gøre dette skal du trække længden fra hver side af ligningen og dividere den med 2.
. For at gøre dette skal du trække længden fra hver side af ligningen og dividere den med 2.
 . For at gøre dette skal du trække længden fra hver side af ligningen og dividere den med 2.
. For at gøre dette skal du trække længden fra hver side af ligningen og dividere den med 2. , træk 16 fra hver side, og divider med 2.
, træk 16 fra hver side, og divider med 2.




4. Skriv det endelige svar ned. Glem ikke at nævne enheden for aflæsningerne.
 og en længde på
og en længde på  , bliver til bredden
, bliver til bredden  .
.Metode 3 af 4: Brug af diagonalen og længden

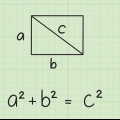
1. Skriv formlen ned for diagonalen af et rektangel. Formlen er  , hvorved
, hvorved  er lig med længden af diagonalen,
er lig med længden af diagonalen,  er lig med længden, og
er lig med længden, og  er lig med rektanglets bredde.
er lig med rektanglets bredde.
 , hvorved
, hvorved  er lig med længden af diagonalen,
er lig med længden af diagonalen,  er lig med længden, og
er lig med længden, og  er lig med rektanglets bredde.
er lig med rektanglets bredde. - Denne metode virker kun for en given længde af diagonalen og længden af den ene side af rektanglet.
- Denne formel er også skrevet som
, hvorved
er lig med højden af rektanglet og bruges i stedet for længden. Variablerne
og
henvise til de samme aflæsninger.

2. Erstat værdierne af diagonalen og siden i formlen. Sørg for at erstatte de korrekte variabler.


3. Kvadret begge sider af formlen. Du skal gøre dette for at slippe af med det radikale tegn, så det bliver lettere at isolere breddevariablen.




4. Isoler variablen w  . Det gør du ved at trække den kvadratiske længde fra hver side af ligningen.
. Det gør du ved at trække den kvadratiske længde fra hver side af ligningen.
 . Det gør du ved at trække den kvadratiske længde fra hver side af ligningen.
. Det gør du ved at trække den kvadratiske længde fra hver side af ligningen. , trække 16 fra hver side.
, trække 16 fra hver side.


5. Løs for w  . Det gør du ved at bestemme kvadratroden for hver side af ligningen.
. Det gør du ved at bestemme kvadratroden for hver side af ligningen.
 . Det gør du ved at bestemme kvadratroden for hver side af ligningen.
. Det gør du ved at bestemme kvadratroden for hver side af ligningen.


6. Skriv det endelige svar ned. Glem ikke at nævne enheden for aflæsningerne.
 og den ene side af
og den ene side af  , bliver til bredden
, bliver til bredden  .
.Metode 4 af 4: Brug af arealet eller omkredsen og relativ længde

1. Skriv formlen ned for arealet eller omkredsen af et rektangel. Hvilken formel du bruger afhænger af de givne måleværdier. Hvis arealet er givet, skal du bruge områdeformlen. Hvis omkredsen er angivet, skal du bruge formlen for omkreds.
- Hvis området eller omkredsen er ukendt, eller forholdet mellem længden og bredden, kan du ikke bruge denne metode.
- Formlen for området er
.
- Formlen for omkredsen er
.
- For eksempel, måske givet at arealet af et rektangel er 24 cm, så bruger du formlen for arealet af et rektangel.

2. Skriv det udtryk, der beskriver sammenhængen mellem længden og bredden. Skriv dit udtryk i en sammenligning med  .
.
 .
. .
.
3. Udskift variablen l  i arealet eller perimeterformlen ved udtrykket for længden. Formlen hører nu kun variablen
i arealet eller perimeterformlen ved udtrykket for længden. Formlen hører nu kun variablen  hvilket betyder at du kan beregne bredden.
hvilket betyder at du kan beregne bredden.
 i arealet eller perimeterformlen ved udtrykket for længden. Formlen hører nu kun variablen
i arealet eller perimeterformlen ved udtrykket for længden. Formlen hører nu kun variablen  hvilket betyder at du kan beregne bredden.
hvilket betyder at du kan beregne bredden. , så ser formlen sådan ud:
, så ser formlen sådan ud:


4. Forenkle ligningen. Den forenklede ligning kan have forskellige former, afhængig af forholdet mellem længden og bredden, og afhængigt af om du går efter arealet eller omkredsen. Prøv at lave en sammenligning, som du  kan løses så nemt som muligt.
kan løses så nemt som muligt.
 kan løses så nemt som muligt.
kan løses så nemt som muligt. så længe
så længe  .
.
5. Løs for w  . Igen, hvordan gør du
. Igen, hvordan gør du  løser afhænger af den forenklede ligning. Brug de grundlæggende regler for algebra og geometri til at løse dette.
løser afhænger af den forenklede ligning. Brug de grundlæggende regler for algebra og geometri til at løse dette.
 . Igen, hvordan gør du
. Igen, hvordan gør du  løser afhænger af den forenklede ligning. Brug de grundlæggende regler for algebra og geometri til at løse dette.
løser afhænger af den forenklede ligning. Brug de grundlæggende regler for algebra og geometri til at løse dette. kan opløses som følger:
kan opløses som følger:

Du har så to mulige løsninger på
 :
: eller
eller  . Da et rektangel ikke kan have en negativ bredde, kan du udelukke -8. Det er din løsning også
. Da et rektangel ikke kan have en negativ bredde, kan du udelukke -8. Det er din løsning også  .
.Artikler om emnet "Bestemmelse af bredden af et rektangel"
Оцените, пожалуйста статью
Lignende
Populær