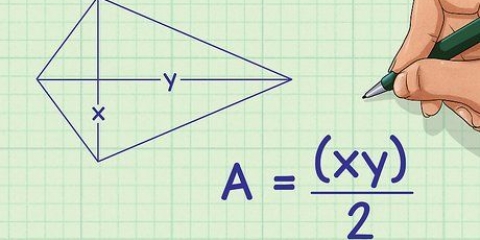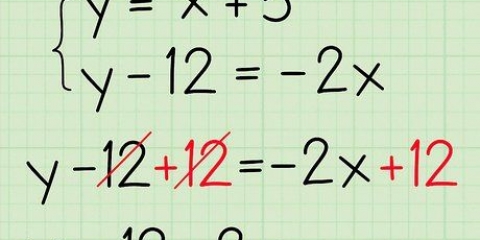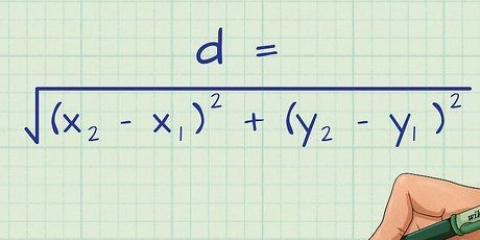For eksempel, hvis bredden af et rektangel er 3 cm og længden er 4 cm, vil din formel se sådan ud:  .
. 
For eksempel:




For eksempel:



Så diagonalen eller et rektangel med en bredde på 3 cm og en længde på 4 cm er 5 cm. 

For eksempel, hvis arealet af rektanglet er 35 kvadratcentimeter, vil din formel se sådan ud:  .
. 
For eksempel:

 .
. 

For eksempel, hvis omkredsen af et rektangel er 24 centimeter, vil din formel se sådan ud:  .
. 
For eksempel:


 .
. 
For eksempel, hvis du fandt med arealformlen, at  , så erstatter du værdien
, så erstatter du værdien  i omkredsformlen:
i omkredsformlen:



For eksempel:




For eksempel:




For eksempel,  er ved at blive
er ved at blive  .
. 
For eksempel ligningen  kan opløses i
kan opløses i  .
. 
For eksempel:


OG

 .
.
Så længden og bredden af rektanglet er 7 cm og 5 cm. 
Du bruger Pythagoras sætning, fordi diagonalen af et rektangel deler det i to kongruente retvinklede trekanter. Bredden og længden af rektanglet er længderne af trekantens sider; diagonalen er trekantens hypotenus. 
For eksempel, hvis du ved, at bredden og længden af rektanglet er 5 cm og 7 cm, vil din formel se sådan ud:  .
. 
For eksempel:




For eksempel:



Så diagonalen af et rektangel med et areal på 35 cm og en omkreds på 24 cm er omkring 8,6 cm. 

Du kan bruge denne metode, hvis du kender omkredsen af rektanglet, bortset fra at du nu bruger omkredsformlen i stedet for arealformlen. Formlen for omkredsen af et rektangel er  , hvorved
, hvorved  er lig med rektanglets bredde, og
er lig med rektanglets bredde, og  er lig med længden af rektanglet.
er lig med længden af rektanglet. 
For eksempel, hvis arealet af rektanglet er 35 kvadratcentimeter, vil din formel se ud som volt:  .
. 
For eksempel hvis du har fundet det  , så erstatter du denne relation
, så erstatter du denne relation  i områdeformlen:
i områdeformlen:



For eksempel:




For eksempel ligningen  kan opløses som
kan opløses som  .
. 
For eksempel:


OG

 .
.
I dette tilfælde er der ét negativt svar. Da længden af et rektangel ikke kan være negativ, ved du, at længden skal være 5 cm. 
Hvis du for eksempel ved, at rektanglets længde er 5 cm, og at forholdet mellem sidernes længder er  , så indtaster du 5 som længde i formlen:
, så indtaster du 5 som længde i formlen:




Du bruger Pythagoras sætning, fordi diagonalen af et rektangel deler det i to kongruente retvinklede trekanter. Bredden og længden af rektanglet er længderne af trekantens sider; diagonalen er trekantens hypotenus. 
For eksempel, hvis du ved, at bredden og længden af rektanglet er lig med 5 cm og 7 cm, ser din formel nu sådan ud:  .
. 
For eksempel:




For eksempel:



Så diagonalen af et rektangel med en bredde, der er 2 cm mere end dets længde, og har et areal på 35 cm, er omkring 8,6 cm.
Beregn længden af diagonalen i et rektangel
Indhold
En diagonal er en lige linje, der forbinder det ene hjørne af et rektangel med det modsatte hjørne. Et rektangel har to diagonaler, hver af samme længde. Hvis du kender længderne af siderne i et rektangel, er det nemt at finde længden af diagonalen ved hjælp af Pythagoras sætning, fordi en diagonal deler et rektangel i to rette trekanter. Hvis du ikke kender længderne af siderne, men du har andre data (såsom arealet og omkredsen eller forholdet mellem længderne af siderne), kan du måle længden og bredden af siderne med en få ekstra trin. find rektanglet, og find derefter længden og bredden af diagonalen ved hjælp af Pythagoras sætning.
Trin
Metode 1 af 3: Brug af længde og bredde

1. Skriv formlen for Pythagoras sætning. Formlen er  , hvorved
, hvorved  og
og  er lig med længderne af siderne i en retvinklet trekant, og
er lig med længderne af siderne i en retvinklet trekant, og  er lig med længden af hypotenusen i en retvinklet trekant.
er lig med længden af hypotenusen i en retvinklet trekant.
 , hvorved
, hvorved  og
og  er lig med længderne af siderne i en retvinklet trekant, og
er lig med længderne af siderne i en retvinklet trekant, og  er lig med længden af hypotenusen i en retvinklet trekant.
er lig med længden af hypotenusen i en retvinklet trekant. - Du bruger Pythagoras sætning, fordi diagonalen af et rektangel deler det i to kongruente retvinklede trekanter. Længden og bredden af rektanglet er længderne af trekantens sider; diagonalen er trekantens hypotenus.

2. Anvend længden og bredden på formlen. Disse er, hvis det er givet korrekt, eller du kan måle dem. Sørg for at erstatte  og
og  .
.
 og
og  .
. .
.
3. Kvadret længden og bredden, og læg derefter disse tal sammen. Kvadring er at gange tallet med sig selv.




4. Træk kvadratroden fra hver side af ligningen fra. Den nemmeste måde at finde en kvadratrod på er at bruge en lommeregner. Du kan bruge en online lommeregner, hvis du ikke har en videnskabelig lommeregner. Dette giver dig værdien  , eller trekantens hypotenus og rektanglets diagonal.
, eller trekantens hypotenus og rektanglets diagonal.
 , eller trekantens hypotenus og rektanglets diagonal.
, eller trekantens hypotenus og rektanglets diagonal.


Så diagonalen eller et rektangel med en bredde på 3 cm og en længde på 4 cm er 5 cm.
Metode 2 af 3: Brug af arealet og omkredsen

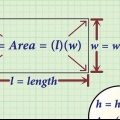
1. Skriv formlen for arealet af et rektangel. Formlen er  , hvorved
, hvorved  er lig med arealet af rektanglet,
er lig med arealet af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde.
 , hvorved
, hvorved  er lig med arealet af rektanglet,
er lig med arealet af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde.
2. Brug arealet af rektanglet i formlen. Sørg for at erstatte den korrekte variabel  .
.
 .
. .
.
3. Omarranger formlen, og du får en værdi for w  . Det gør du ved at dividere begge sider af ligningen med
. Det gør du ved at dividere begge sider af ligningen med  . Sæt denne værdi til side. Du vil bruge dette senere i formlen for omkredsen.
. Sæt denne værdi til side. Du vil bruge dette senere i formlen for omkredsen.
 . Det gør du ved at dividere begge sider af ligningen med
. Det gør du ved at dividere begge sider af ligningen med  . Sæt denne værdi til side. Du vil bruge dette senere i formlen for omkredsen.
. Sæt denne værdi til side. Du vil bruge dette senere i formlen for omkredsen.
 .
.
4. Skriv formlen for omkredsen af et rektangel. Formlen er  , hvorved
, hvorved  er lig med rektanglets bredde, og
er lig med rektanglets bredde, og  er lig med længden af rektanglet.
er lig med længden af rektanglet.
 , hvorved
, hvorved  er lig med rektanglets bredde, og
er lig med rektanglets bredde, og  er lig med længden af rektanglet.
er lig med længden af rektanglet.
5. Brug værdien af omkredsen i formlen. Sørg for at erstatte variablen  .
.
 .
. .
.
6. Divider begge sider af ligningen med 2. Dette giver dig værdien  .
.
 .
.

 .
.
7. Brug værdien w  i ligningen. Brug den værdi, du fandt, ved at omarrangere arealformlen.
i ligningen. Brug den værdi, du fandt, ved at omarrangere arealformlen.
 i ligningen. Brug den værdi, du fandt, ved at omarrangere arealformlen.
i ligningen. Brug den værdi, du fandt, ved at omarrangere arealformlen. , så erstatter du værdien
, så erstatter du værdien  i omkredsformlen:
i omkredsformlen:


8. Eliminer brøken i ligningen. Det gør du ved at gange begge sider af ligningen med  .
.
 .
.



9. Indstil ligningen lig med 0. Det gør du ved at trække førstegradsleddet fra begge sider af ligningen.




10. Omarranger rækkefølgen af led i ligningen. Det betyder, at udtrykket med eksponenten kommer først, efterfulgt af udtrykket med variablen og til sidst konstanten. Når du omarrangerer, skal du være opmærksom på de korrekte positive og negative tegn. Ligningen er nu ordnet som andengradsligning.
 er ved at blive
er ved at blive  .
.
11. Faktorer den andengradsligning. For detaljerede instruktioner om, hvordan du gør dette, læs artiklen Løs andengradsligninger.
 kan opløses i
kan opløses i  .
.
12. Bestem værdierne af l  . Det gør du ved at sætte hvert led til nul og løse for variablen. Du får to løsninger til denne ligning. Da du har at gøre med et rektangel, vil de to løsninger være bredden og længden af dit rektangel.
. Det gør du ved at sætte hvert led til nul og løse for variablen. Du får to løsninger til denne ligning. Da du har at gøre med et rektangel, vil de to løsninger være bredden og længden af dit rektangel.
 . Det gør du ved at sætte hvert led til nul og løse for variablen. Du får to løsninger til denne ligning. Da du har at gøre med et rektangel, vil de to løsninger være bredden og længden af dit rektangel.
. Det gør du ved at sætte hvert led til nul og løse for variablen. Du får to løsninger til denne ligning. Da du har at gøre med et rektangel, vil de to løsninger være bredden og længden af dit rektangel.

OG

 .
.Så længden og bredden af rektanglet er 7 cm og 5 cm.

13. Skriv formlen for Pythagoras sætning. Formlen er  , hvorved
, hvorved  og
og  er lig med længderne af siderne i en retvinklet trekant, og
er lig med længderne af siderne i en retvinklet trekant, og  er lig med længden af hypotenusen i en retvinklet trekant.
er lig med længden af hypotenusen i en retvinklet trekant.
 , hvorved
, hvorved  og
og  er lig med længderne af siderne i en retvinklet trekant, og
er lig med længderne af siderne i en retvinklet trekant, og  er lig med længden af hypotenusen i en retvinklet trekant.
er lig med længden af hypotenusen i en retvinklet trekant.
14. Brug bredde- og længdegraden i formlen. Det er lige meget, hvilken værdi du bruger til hvilken variabel.
 .
.
15. Kvadret bredde- og længdegraden, og læg derefter disse tal sammen. At kvadre betyder at gange et tal med sig selv.




16. Tag kvadratroden af hver side af ligningen. Den nemmeste måde at finde en kvadratrod på er ved at bruge en lommeregner. Du kan bruge en online lommeregner, hvis du ikke har en videnskabelig lommeregner. Dette giver dig værdien  , og det er hypotenusen af trekanten og diagonalen af rektanglet.
, og det er hypotenusen af trekanten og diagonalen af rektanglet.
 , og det er hypotenusen af trekanten og diagonalen af rektanglet.
, og det er hypotenusen af trekanten og diagonalen af rektanglet.


Så diagonalen af et rektangel med et areal på 35 cm og en omkreds på 24 cm er omkring 8,6 cm.
Metode 3 af 3: Brug af sidernes areal og relationelle længder

1. Skriv en formel, der forklarer sammenhængen mellem længderne af siderne. Du kan ændre længden ( ) eller bredden (
) eller bredden ( ) isolere. Læg denne formel til side et øjeblik. Du vil snart bruge det i overfladeformlen.
) isolere. Læg denne formel til side et øjeblik. Du vil snart bruge det i overfladeformlen.
 ) eller bredden (
) eller bredden ( ) isolere. Læg denne formel til side et øjeblik. Du vil snart bruge det i overfladeformlen.
) isolere. Læg denne formel til side et øjeblik. Du vil snart bruge det i overfladeformlen. - For eksempel, hvis du ved, at bredden af et rektangel er 2 cm mere end dets længde, kan du skrive en formel som f.eks
:
.

2. Skriv formlen for arealet af et rektangel. Formlen er  , hvorved
, hvorved  er lig med arealet af rektanglet,
er lig med arealet af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde.
 , hvorved
, hvorved  er lig med arealet af rektanglet,
er lig med arealet af rektanglet,  er lig med længden af rektanglet, og
er lig med længden af rektanglet, og  er lig med rektanglets bredde.
er lig med rektanglets bredde. , hvorved
, hvorved  er lig med rektanglets bredde, og
er lig med rektanglets bredde, og  er lig med længden af rektanglet.
er lig med længden af rektanglet.
3. Brug arealet af rektanglet i formlen. Sørg for at erstatte variablen  .
.
 .
. .
.
4. Brug relationsformlen for længden (eller bredden) i formlen. Da du har at gøre med et rektangel, er det lige meget, om du arbejder med variabel  eller
eller  .
.
 eller
eller  .
. , så erstatter du denne relation
, så erstatter du denne relation  i områdeformlen:
i områdeformlen:


5. Gør det til en andengradsligning. Det gør du ved at bruge den fordelende egenskab og gange led i parentes sammen, hvorefter du sætter ligningen lig med 0.




6. Faktorer den andengradsligning. For detaljerede instruktioner om, hvordan du gør dette, læs artiklen Løs andengradsligninger.
 kan opløses som
kan opløses som  .
.
7. Bestem værdierne af l  . Det gør du ved at gøre hvert led lig med nul og løse for variablen. Du finder to løsninger til ligningen.
. Det gør du ved at gøre hvert led lig med nul og løse for variablen. Du finder to løsninger til ligningen.
 . Det gør du ved at gøre hvert led lig med nul og løse for variablen. Du finder to løsninger til ligningen.
. Det gør du ved at gøre hvert led lig med nul og løse for variablen. Du finder to løsninger til ligningen.

OG

 .
.I dette tilfælde er der ét negativt svar. Da længden af et rektangel ikke kan være negativ, ved du, at længden skal være 5 cm.

8. Brug værdien af længden (eller bredden) i din relationsformel. Dette vil give dig længden af den anden side af rektanglet.
 , så indtaster du 5 som længde i formlen:
, så indtaster du 5 som længde i formlen:



9. Skriv formlen for Pythagoras sætning. Formlen er  , hvorved
, hvorved  og
og  er lig med længderne af siderne i en retvinklet trekant, og
er lig med længderne af siderne i en retvinklet trekant, og  er lig med længden af hypotenusen i en retvinklet trekant.
er lig med længden af hypotenusen i en retvinklet trekant.
 , hvorved
, hvorved  og
og  er lig med længderne af siderne i en retvinklet trekant, og
er lig med længderne af siderne i en retvinklet trekant, og  er lig med længden af hypotenusen i en retvinklet trekant.
er lig med længden af hypotenusen i en retvinklet trekant.
10. Brug bredde- og længdegraden i formlen. Det er lige meget, hvilken værdi du bruger til hvilken variabel.
 .
.
11. Kvadret bredde- og længdegraden, og læg derefter disse tal sammen. At kvadre betyder at gange et tal med sig selv.




12. Træk kvadratroden fra hver side af ligningen fra. Den nemmeste måde at finde en kvadratrod på er ved at bruge en lommeregner. Du kan bruge en online lommeregner, hvis du ikke har en videnskabelig lommeregner. Dette giver dig værdien  , eller trekantens hypotenus og dermed rektanglets diagonal.
, eller trekantens hypotenus og dermed rektanglets diagonal.
 , eller trekantens hypotenus og dermed rektanglets diagonal.
, eller trekantens hypotenus og dermed rektanglets diagonal.


Så diagonalen af et rektangel med en bredde, der er 2 cm mere end dets længde, og har et areal på 35 cm, er omkring 8,6 cm.
Artikler om emnet "Beregn længden af diagonalen i et rektangel"
Оцените, пожалуйста статью
Lignende
Populær