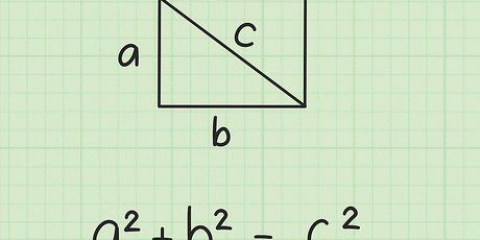
X-aksen er den vandrette akse; y-aksen er den lodrette akse. Koordinaterne for et punkt skrives som  .
. For eksempel kan et linjestykke have et endepunkt ved  og en anden på
og en anden på  .
. 
For eksempel med pointerne  og
og  , din formel vil se sådan ud:
, din formel vil se sådan ud: 


For eksempel:



For eksempel:



Da du bestemmer kvadratroden, skal du muligvis afrunde dit svar. Da du arbejder ud fra et koordinatsystem, vil dit svar være generelt "enheder" og ikke i centimeter, meter eller nogen anden enhed. For eksempel:

 enheder.
enheder.
Beregning af længden af en linje ved hjælp af afstandsformlen
Du kan måle længden af en lodret eller vandret linje i et koordinatsystem ved blot at tilføje koordinaterne; det er dog lidt vanskeligere at måle længden af en diagonal linje. Du kan bruge afstandsformlen til at bestemme længden af en sådan linje. Denne formel er faktisk Pythagoras sætning, som bliver tydelig, når du forestiller dig linjestykket som hypotenusen af en retvinklet trekant. Ved at bruge en simpel geometrisk formel bliver måling af linjer langs en række koordinater en forholdsvis enkel opgave.
Trin
Del 1 af 2: Skrivning af formlen

1. Skriv afstandsformlen ned. Formlen siger det  , hvorved
, hvorved  er lig med linjens afstand,
er lig med linjens afstand,  er lig med koordinaterne for det første endepunkt af linjestykket, og
er lig med koordinaterne for det første endepunkt af linjestykket, og  er lig med koordinaterne for det andet endepunkt af linjestykket.
er lig med koordinaterne for det andet endepunkt af linjestykket.
 , hvorved
, hvorved  er lig med linjens afstand,
er lig med linjens afstand,  er lig med koordinaterne for det første endepunkt af linjestykket, og
er lig med koordinaterne for det første endepunkt af linjestykket, og  er lig med koordinaterne for det andet endepunkt af linjestykket.
er lig med koordinaterne for det andet endepunkt af linjestykket.
2. Bestem koordinaterne for endepunkterne i linjestykket. Disse er muligvis allerede givet. Hvis ikke, tæl langs x-aksen og y-aksen for at finde koordinaterne.
 .
. og en anden på
og en anden på  .
.
3. Anvend koordinaterne til afstandsformlen. Sørg for at indtaste værdierne for de korrekte variable. De to  -koordinater er inden for den første parentes, og de to
-koordinater er inden for den første parentes, og de to  -koordinaterne er inden for de næste to parenteser.
-koordinaterne er inden for de næste to parenteser.
 -koordinater er inden for den første parentes, og de to
-koordinater er inden for den første parentes, og de to  -koordinaterne er inden for de næste to parenteser.
-koordinaterne er inden for de næste to parenteser. og
og  , din formel vil se sådan ud:
, din formel vil se sådan ud: 
Del 2 af 2: Beregning af afstanden

1. Beregn minussummen i parentes. I henhold til rækkefølgen af operationer skal hver udregning i parentes beregnes først.
- For eksempel:

2. Kvadret værdien i parentes. Operationsrækkefølgen siger, at man så skal beregne potenserne.



3. Tilføj tallene under det radikale tegn. Du kan lave denne beregning, som om du arbejdede med heltal.



4. Løs for d  . For at tilnærme det endelige svar, find kvadratroden af summen under radikalet.
. For at tilnærme det endelige svar, find kvadratroden af summen under radikalet.
 . For at tilnærme det endelige svar, find kvadratroden af summen under radikalet.
. For at tilnærme det endelige svar, find kvadratroden af summen under radikalet.
 enheder.
enheder.Tips
- Forveksle ikke denne formel med andre, såsom midtpunktsformlen, hældningsformlen eller ligningen for en linje.
- Husk rækkefølgen af operationer, når du beregner svaret. Træk først fra, derefter kvadratisk forskellen, addér og beregn derefter kvadratroden.
Artikler om emnet "Beregning af længden af en linje ved hjælp af afstandsformlen"
Оцените, пожалуйста статью
Populær