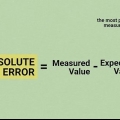
Beregning af den absolutte værdi af et tal: 15 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Bestem den absolutte værdi
- Metode 2 af 2: Løsning af komplekse ligninger med absolutte værdier (ligninger med `i`)
Tips

Den absolutte værdi af et tal er let at finde, og teorien bag det er vigtig for at løse ligninger med en absolut værdi. Hver absolut værdi er et mål for, hvor langt dette tal er fra nul. Hvis du tænker på en tallinje, med nullet i midten, kan du finde ud af, hvor langt væk det pågældende tal er fra dette nul.

Trin

Metode 1 af 2: Bestem den absolutte værdi

1. Husk, at den absolutte værdi er afstanden mellem et tal og nul. En absolut værdi er afstanden fra tallet til nul langs en tallinje. enten,

| - 4 |

${displaystyle |-4|}$ så angiver blot, hvor langt væk -4 er fra nul. Da afstand altid er et positionsnummer (du kan ikke bevæge dig i `negative` trin, bare i en anden retning), er resultatet af den absolutte værdi altid positivt.

Billede med titlen Find den absolutte værdi af et tal Trin 2

2. Gør tallet inden for de absolutte værdisøjler positivt. Kort sagt gør den absolutte værdi ethvert tal positivt. Det er nyttigt til at måle afstand eller bestemme værdier i økonomiske anliggender, arbejde med negative tal såsom gæld eller lån.

Billede med titlen Find den absolutte værdi af et tal Trin 3

3. Brug enkle, lodrette streger til at angive en absolut værdi. Formatet for en absolut værdi er nemt. Enkelte linjer (findes i nærheden af Enter-tasten på et tastatur) omkring et tal eller udtryk, som f.eks

| n |, | 3 + 5 |, | - 72 |

${displaystyle |n|,|3+5|,|-72|}$ , angiver en absolut værdi.

| 2 |

${displaystyle |2|}$ er `den absolutte værdi af 2.`

Billede med titlen Find den absolutte værdi af et tal Trin 4

4. Udelad minustegn for tallet inden for de absolutte værdimærker. For eksempel: |-5| bliver så |5|.

Billede med titlen Find den absolutte værdi af et tal Trin 5

5. Udelad de absolutte værdimærker. Det tal, der er tilbage, er svaret, så |-5| bliver |5| og så 5. Følgende er alt, hvad du skal gøre:

| - 5 | = 5

${displaystyle |-5|=5}$

Billede med titlen Find den absolutte værdi af et tal Trin 6

6. Forenkle udtrykket inden for den absolutte værdi. Er det et simpelt udtryk, som f.eks

| - 10 |

${displaystyle |-10|}$ , så kan du bare gøre det positivt. Men et udtryk som

| (- 4 * 5) + 3 - 2 |

${displaystyle |(-4*5)+3-2|}$ skal forenkles, før du kan finde dens absolutte værdi. Den faste rækkefølge af operationer gælder stadig:

Opgave:

| (- 4 * 5) + 3 - 2 |

${displaystyle |(-4*5)+3-2|}$

Forenklet inden for parentes:

| (- 20) + 3 - 2 |

${displaystyle |(-20)+3-2|}$

Tilføj og subtraher:

| - 19 |

${displaystyle |-19|}$

Gør alt inden for den absolutte værdi positivt:

| 19 |

${displaystyle |19|}$

Sidste svar: 19

Billede med titlen Find den absolutte værdi af et tal Trin 7

7. Brug altid denne rækkefølge af operationer, før du beregner den absolutte værdi. Når du udarbejder længere ligninger, udfører du alt det nødvendige arbejde, før du bestemmer den absolutte værdi. Forsøg ikke at forenkle absolutte værdier, før alt er tilføjet, trukket fra og divideret korrekt. For eksempel:

Opgave:

1 + 2 + | 4 - 7 | 5 * | - 3 * 2 |

${displaystyle {frac {1+2+|4-7|}{5*|-3*2|}}}$

Udfør rækkefølgen af operationer inden for og uden for den absolutte værdi:

3 + | - 3 | 5 * | - 6 |

${displaystyle {frac {3+|-3|}{5*|-6|}}}$

Bestem de absolutte værdier:

3 + (3) 5 * (6)

${displaystyle {frac {3+(3)}{5*(6)}}}$

Operationsrækkefølge:

\frac{6}{30}

${displaystyle {frac {6}{30}}}$

Forenkle det endelige svar: $\frac{1}{5}$ ${frac{1}{5}}$

Billede med titlen Find den absolutte værdi af et tal Trin 8

8. Fortsæt med at arbejde på et par prøveøvelser for at få styr på det. Det er meget nemt at beregne den absolutte værdi af et tal, men det betyder ikke, at det ikke ville være nyttigt at lave øvelsesproblemer til at opfriske din viden:

| 12 |

${displaystyle |12|}$ =

12

${displaystyle 12}$

| - 24 |

${displaystyle |-24|}$ =

24

${displaystyle 24}$

| 3 + 2 - 11 + 5 - 6 |

${displaystyle |3+2-11+5-6|}$ =

7

$7$

Metode 2 af 2: Løsning af komplekse ligninger med absolutte værdier (ligninger med `i`)

Billede med titlen Find den absolutte værdi af et tal Trin 9

1. Vær forsigtig, når du har at gøre med komplekse ligninger, der involverer imaginære tal, såsom `i` eller -1{displaystyle {sqrt {-1}}} ${displaystyle {sqrt {-1}}}$ , og løse dem separat. Man kan ikke finde den absolutte værdi af imaginære tal på samme måde, som man kan finde rationelle tal. Du kan finde den absolutte værdi af en kompleks ligning ved at regne den ud i afstandsformlen. Tag udtrykket

| 3 - 4 jeg |

${displaystyle |3-4i|}$ som et eksempel.

Opgave: $| 3 - 4 jeg |$ ${displaystyle |3-4i|}$
Vær opmærksom: Hvis du bruger et udtryk som $\sqrt{- 1}$ ${displaystyle {sqrt {-1}}}$ du kan erstatte det med `i.`Kvadratroden af -1 er et imaginært tal, dvs. $| jeg | = 1$ ${displaystyle |i|=1}$

Billede med titlen Find den absolutte værdi af et tal Trin 10

2. Find koefficienterne for den komplekse ligning. Tag 3-4i som ligningen for en linje. Den absolutte værdi er afstanden til nul, så du bestemmer afstanden til nul for punktet (3, -4) på denne linje.Koefficienterne er simpelthen de to tal, der ikke er `i`. Selvom tallet ved siden af i`et normalt er det andet tal, er det lige meget, når man løser. Øv dette med følgende koefficienter:

| 1 + 6 jeg |

${displaystyle |1+6i|}$ = (1, 6)

| 2 - jeg |

${displaystyle |2-i|}$ = (2, -1)

| 6 jeg - 8 |

${displaystyle |6i-8|}$ = (-8, 6)

Billede med titlen Find den absolutte værdi af et tal Trin 11

3. Fjern de absolutte værdisymboler fra ligningen. Du mangler nu kun koefficienterne. Husk at du bestemmer ligningens afstand fra nul. Da du vil bruge afstandsformlen i næste trin, er dette det samme som at bestemme den absolutte værdi.

Billede med titlen Find den absolutte værdi af et tal Trin 12

4. Kvadret begge koefficienter. For at bestemme afstanden bruger du afstandsformlen, også kendt som

\sqrt{x} 2 + y^{2}

${displaystyle {sqrt {x^{2}+y^{2}}}}$ . Så som et første skridt skal du kvadrere begge koefficienter af den komplekse ligning. Vi fortsætter med eksemplet:

| 3 - 4 jeg |

${displaystyle |3-4i|}$ :

Koefficienter: (3, -4)

Afstandsformel:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Kvadrate koefficienterne: `

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Vær opmærksom: Øv afstandsformlen igen, hvis du ikke forstår den. Bemærk, at kvadrering af begge tal gør dem positive, hvilket i det væsentlige giver dig den absolutte værdi.

Billede med titlen Find den absolutte værdi af et tal Trin 13

5. Placer produktet af tallene under radikalet. Det radikale tegn indikerer, at du trækker kvadratroden af tallet under det. Læg nu tallene sammen først, uden at gøre noget ved det radikale tegn.

Koefficienter: (3, -4)

Afstandsformel:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Kvadrate koefficienterne:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Læg produktet af koefficienterne sammen:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Billede med titlen Find den absolutte værdi af et tal Trin 14

6. Tag kvadratroden for dit endelige svar. Du skal blot forenkle ligningen for det endelige svar. Dette er afstanden fra dit `punkt` på en imaginær tallinje til nulpunktet. Hvis der ikke er nogen kvadratrod, skal du blot lade svaret fra sidste trin stå under det radikale tegn - dette er et korrekt svar.

Koefficienter: (3, -4)

Afstandsformel:

\sqrt{3} 2 + (- 4)^{2}

${displaystyle {sqrt {3^{2}+(-4)^{2}}}}$

Kvadrate koefficienterne:

\sqrt{9 + 16}

${displaystyle {sqrt {9+16}}}$

Læg produktet af koefficienterne sammen:

\sqrt{25}

${displaystyle {sqrt {25}}}$

Træk kvadratroden fra for det endelige svar: 5

$| 3 - 4 jeg | = 5$ ${displaystyle |3-4i|=5}$

Billede med titlen Find den absolutte værdi af et tal Trin 15

7. Prøv nogle øvelser. Klik med musen direkte bag spørgsmålene for at se svarene i hvidt.

| 1 + 6 jeg |

${displaystyle |1+6i|}$ = √37

| 2 - jeg |

${displaystyle |2-i|}$ = √5

| 6 jeg - 8 |

${displaystyle |6i-8|}$ = 10

Tips

Hvis du har en variabel inden for en absolut værdi, kan du ikke fjerne de absolutte værditegn ved hjælp af denne metode, for hvis værdien af variablen er negativ, vil den absolutte værdi gøre den positiv.
Hvis du har et udtryk inden for en absolut værdi, skal du forenkle udtrykket, før du bestemmer dets absolutte værdi.
Når et positivt tal er inden for de absolutte værdimarkører, er svaret altid det tal.
Du har brug for en anden metode til at løse absolutværdiligninger med x og y, selvom teorien bag den absolutte værdi bruges som grundlag.
En absolut værdi kan aldrig være et negativt tal, så hvis du ser noget som | 2 - 4x| = -7, så ved du, at denne ligning er falsk uden at skulle løse den.