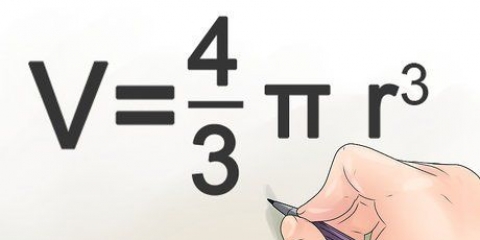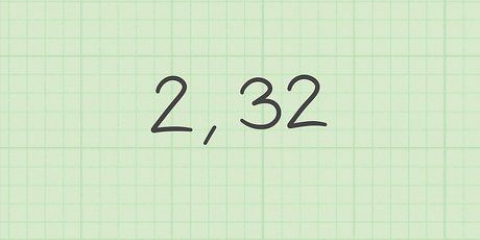Beregning af Fibonacci-sekvensen (med billeder)

Indhold

Trin
- Metode 1 af 2: Brug en tabel
- Metode 2 af 2: Brug af Binets formel og den gyldne middelvej

Fibonacci-sekvensen er en sekvens af tal genereret ved at tilføje de to foregående numre i sekvensen. Tallene i serien ses hyppigt i naturen og i kunsten, såsom spiraler og det gyldne snit. Den nemmeste måde at beregne serien på er at udarbejde en tabel; dette er dog ikke praktisk, hvis du for eksempel leder efter det 100. led i rækkefølgen, i hvilket tilfælde du vil bruge Binets formel.

Trin

Metode 1 af 2: Brug en tabel

1. Lav en tabel med to kolonner. Antallet af rækker afhænger af antallet af tal i den Fibonacci-sekvens, du vil beregne.

For eksempel, hvis du vil finde det femte tal i rækkefølgen, vil din tabel have fem rækker.
Med denne tabelmetode er det ikke muligt at finde et tal længere nede i rækkefølgen uden først at beregne alle tallene før det. For eksempel, hvis du vil finde det 100. tal i rækken, skal du først finde de første 99 tal. Derfor virker tabelmetoden kun for tal i begyndelsen af sekvensen.

Billede med titlen Beregn Fibonacci-sekvensen Trin 2

2. Indtast rækkefølgen af tal i venstre kolonne. Det betyder, at du skal udfylde en række af på hinanden følgende ordenstal, begyndende med "1."

Udtrykket refererer til nummerets position i Fibonacci-sekvensen.

For eksempel, hvis du vil beregne det femte tal i rækkefølgen, vil du skrive 1., 2., 3., 4., 5. nede i venstre kolonne. Dette vil hjælpe dig med at identificere de første fem led i sekvensen.

Billede med titlen Beregn Fibonacci-sekvensen Trin 3

3. Sæt 1 i den første række i højre kolonne. Dette er udgangspunktet for Fibonacci-sekvensen. Med andre ord er det første led i rækkefølgen 1.

Den korrekte Fibonacci-sekvens starter altid med 1. Hvis du vil starte med et andet tal, finder du ikke det korrekte mønster af Fibonacci-sekvensen.

Billede med titlen Beregn Fibonacci-sekvensen Trin 4

4. Tæl det første led (1) og 0. sammen på. Dette vil give dig det andet nummer i rækkefølgen.

Husk, at for at finde et givet nummer af Fibonacci-sekvensen, skal du blot lægge de to foregående tal sammen.

For at skabe sekvensen kommer 0 før 1 (det første led), så: 1 + 0 = 1.

Billede med titlen Beregn Fibonacci-sekvensen Trin 5

5. Læg det første led (1) og det andet led (1) sammen. Dette vil give dig det tredje nummer i rækkefølgen.

1 + 1 = 2. Tredje semester er 2.

Billede med titlen Beregn Fibonacci-sekvensen Trin 6

6. Læg det andet led (1) og det tredje led (2) sammen for at få det fjerde tal i rækkefølgen.

1 + 2 = 3. Fjerde semester er 3.

Billede med titlen Beregn Fibonacci-sekvensen Trin 7

7. Læg det tredje led (2) og det fjerde led (3) sammen. Nu kender du det femte tal i rækken.

2 + 3 = 5. Den femte periode er 5.

Billede med titlen Beregn Fibonacci-sekvensen Trin 8

8. Læg de to foregående tal sammen for at finde et givet tal i Fibonacci-sekvensen. Hvis du bruger denne metode, bruger du formlen

f n = f_{n - 1} + f_{n - 2}

$F_{{n}}=F_{{n-1}}+F_{{n-2}}$ . Fordi dette ikke er en lukket formel, kan du ikke bruge den til at beregne hvert led i rækken uden først at beregne alle de foregående tal.

Metode 2 af 2: Brug af Binets formel og den gyldne middelvej

Billede med titlen Beregn Fibonacci-sekvensen Trin 9

1. Skriv formlen ned:

x n

$x_{{n}}$ =

φ n - (1 - φ)^{n} \sqrt{5}

${frac{phi ^{{n}}-(1-phi )^{{n}}}{{sqrt{5}}}}$ . I formlen,

x n

$x_{{n}}$ = udtrykket i den rækkefølge, du forsøger at finde,

n

$n$ = positionsnummeret for udtrykket i rækken, og

φ

$phi$ = det gyldne snit.

Dette er en lukket formel, så du kan beregne et bestemt led i serien uden at skulle beregne alle de foregående.
Denne formel er en forenklet formel, der stammer fra Binets Fibonacci-formel.
Formlen anvender det gyldne snit ( $φ$ $phi$ ), fordi forholdet mellem to på hinanden følgende tal i Fibonacci-sekvensen er meget lig det gyldne snit.

Billede med titlen Beregn Fibonacci-sekvensen Trin 10

2. Juster tallet for n{displaystyle n} $n$ gælder for formlen. Det

n

$n$ repræsenterer det udtryk, du leder efter i sekvensen.

Hvis du f.eks. leder efter det femte tal i rækkefølgen, skal du indtaste 5. Din formel skulle nu se sådan ud:

x 5

$x_{{5}}$ =

φ 5 - (1 - φ)^{5} \sqrt{5}

${frac{phi ^{{5}}-(1-phi )^{{5}}}{{sqrt{5}}}}$ .

Billede med titlen Beregn Fibonacci-sekvensen Trin 11

3. Erstat det gyldne snit i formlen. Brug 1,618034 som en tilnærmelse af det gyldne snit.

Hvis du f.eks. søger efter det femte tal i rækkefølgen, vil formlen, du indtastede, se sådan ud:

x 5

$x_{{5}}$ =

(1, 618034) 5 - (1 - 1, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(1-1,618034)^{{5}}}{{sqrt{5}}}}$ .

Billede med titlen Beregn Fibonacci-sekvensen Trin 12

4. Udfør beregningerne i parentes. Overvej rækkefølgen af aritmetiske operationer ved først at beregne delen i parentes:

1 - 1, 618034 = - 0, 618034

$1-1,618034=-0,618034$ .

I eksemplet bliver ligningen

x 5

$x_{{5}}$ =

(1, 618034) 5 - (- 0, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(-0.618034)^{{5}}}{{sqrt{5}}}}$ .

Billede med titlen Beregn Fibonacci-sekvensen Trin 13

5. Beregn eksponenterne. Gang de to tal i parentes i tælleren med den relevante eksponent.

I eksemplet,

1, 618034 5 = 11, 090170

$1,618034^{{5}}=11,090170$ ;

- 0, 618034 5 = - 0, 090169

$-0,618034^{{5}}=-0,090169$ . Så ligningen bliver

x 5 = 11, 090170 - (- 0, 090169) \sqrt{5}

$x_{{5}}={frac{11,090170-(-0.090169)}{{sqrt{5}}}}$ .

Billede med titlen Beregn Fibonacci-sekvensen Trin 14

6. Fuldfør beregningen. Før du fortsætter med at dividere, skal du først trække de to tal i tælleren fra.

I eksemplet,

11, 090170 - (- 0, 090169) = 11, 180339

$11,090170-(-0,090169)=11,180339$ , så ligningen bliver

x 5

$x_{{5}}$ =

11, 180339 \sqrt{5}

${frac{11,180339}{{sqrt{5}}}}$ .

Billede med titlen Beregn Fibonacci-sekvensen Trin 15

7. Divider med kvadratroden af fem. Kvadratroden af fem er afrundet til 2,236067.

I eksempelopgaven,

11, 180339 2, 236067 = 5, 000002

${frac{11,180339}{2,236067}}=5,000002$ .

Billede med titlen Beregn Fibonacci-sekvensen Trin 16

8. Afrund til nærmeste hele tal. Dit svar er et decimaltal, men er meget tæt på et heltal. Dette heltal repræsenterer tallet i Fibonacci-sekvensen.

Hvis du har brugt det fulde gyldne snit og ikke har afrundet noget, får du et helt tal. Det er dog mere praktisk at afrunde, hvilket vil resultere i en decimal.

I eksemplet vil dit svar, beregnet med en lommeregner, være cirka 5.000002. Afrundet til nærmeste hele tal vil dit svar være fem, hvilket også vil være det femte tal i Fibonacci-sekvensen.