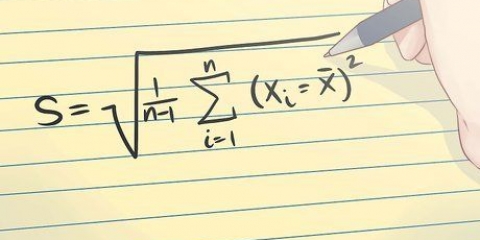Beregning af summen af kvadrater (sse)

Indhold

Trin

Summen af kvadrater, eller SSE, er en foreløbig statistisk beregning, der fører til forskellige dataværdier. Når du har et sæt af dataværdier, er det nyttigt at kunne bestemme, hvor tæt disse værdier er relateret til hinanden. Du skal organisere dine data i en tabel og derefter lave nogle ret simple beregninger. Når du har fundet SSE`en for et datasæt, kan du finde variansen og standardafvigelsen.

Trin

Metode 1 af 3: Beregn SSE i hånden

1. Lav en tabel med tre kolonner. Den nemmeste måde at beregne SSE på er at starte med en tabel med tre kolonner. Mærk de tre kolonner

Hvor er

${displaystyle {text{Værdi}}}$ ,

afvigelse

${displaystyle {text{Afvigelse}}}$ , og

afvigelse 2

${displaystyle {text{Afvigelse}}^{2}}$ .

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 2

2. Udfyld detaljerne. Den første kolonne indeholder værdierne af dine målinger. Udfyld kolonnen

Hvor er

${displaystyle {text{Værdi}}}$ med dine aflæsninger. Dette kan være resultaterne af et eksperiment, en statistisk undersøgelse eller blot data fra et matematisk problem.

Antag i dette tilfælde, at du arbejder med medicinske data, og at du har en liste over kropstemperaturerne for ti patienter. Den forventede normale kropstemperatur er 98,6 grader. Temperaturen på ti patienter måles og giver værdierne 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 og 99,1. Temperaturen på ti patienter måles og giver værdierne 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 og 99,1. Skriv disse værdier i den første kolonne.

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 3

3. Beregn gennemsnittet. Før du kan beregne fejlen for hver måling, skal du beregne middelværdien af hele datasættet.

Middelværdien af et datasæt er summen af dets værdier divideret med antallet af værdier i sættet. Dette kan repræsenteres symbolsk med variablen

μ

$mu$ :

μ = Σ x n

${displaystyle mu ={frac {Sigma x}{n}}}$

For disse data beregnes gennemsnittet som følger:

μ = 99, 0 + 98, 6 + 98, 5 + 101, 1 + 98, 3 + 98, 6 + 97, 9 + 98, 4 + 99, 2 + 99, 1 10

${displaystyle mu ={frac {99.0+98.6+98.5+101.1+98.3+98.6+97.9+98.4+99.2+99.1} {10}}}$

μ = 988, 7 10

${displaystyle mu ={frac {988.7}{10}}}$

μ = 98, 87

${displaystyle mu =98,87}$

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 4

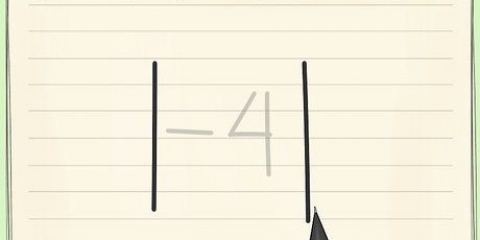
4. Beregn de enkelte fejlværdier. I den anden kolonne i din tabel skal du indtaste fejlværdierne for hver dataværdi. Fejlen er forskellen mellem aflæsningen og middelværdien.

For det givne datasæt skal du trække middelværdien, 98,87, fra hver målt værdi og udfylde den anden kolonne med resultaterne. Disse ti beregninger går sådan her:

99, 0 - 98, 87 = 0, 13

${displaystyle 99.0-98.87=0.13}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98.6-98.87=-0.27}$

98, 5 - 98, 87 = - 0, 37

${displaystyle 98.5-98.87=-0.37}$

101, 1 - 98, 87 = 2, 23

${displaystyle 101.1-98.87=2.23}$

98, 3 - 98, 87 = - 0, 57

${displaystyle 98.3-98.87=-0.57}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98.6-98.87=-0.27}$

97, 9 - 98, 87 = - 0, 97

${displaystyle 97.9-98.87=-0.97}$

98, 4 - 98, 87 = - 0, 47

${displaystyle 98.4-98.87=-0.47}$

99, 2 - 98, 87 = 0, 33

${displaystyle 99.2-98.87=0.33}$

99, 1 - 98, 87 = 0, 23

${displaystyle 99.1-98.87=0.23}$

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 5

5. Beregn SSE. I den tredje kolonne i tabellen skal du finde kvadratet af hver af de resulterende værdier i den midterste kolonne. Disse repræsenterer kvadraterne af afvigelsen fra middelværdien for hver målt dataværdi.

For hver værdi i den midterste kolonne skal du bruge en lommeregner til at beregne kvadratet. Registrer resultaterne i den tredje kolonne, som følger:

0, 13 2 = 0, 0169

${displaystyle 0,13^{2}=0,0169}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0,27)^{2}=0,0729}$

(- 0, 37) 2 = 0, 1369

${displaystyle (-0,37)^{2}=0,1369}$

2, 23 2 = 4, 9729

${displaystyle 2.23^{2}=4.9729}$

(- 0, 57) 2 = 0, 3249

${displaystyle (-0,57)^{2}=0,3249}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0,27)^{2}=0,0729}$

(- 0, 97) 2 = 0, 9409

${displaystyle (-0,97)^{2}=0,9409}$

(- 0, 47) 2 = 0, 2209

${displaystyle (-0,47)^{2}=0,2209}$

0, 33 2 = 0, 1089

${displaystyle 0,33^{2}=0,1089}$

0, 23 2 = 0, 0529

${displaystyle 0,23^{2}=0,0529}$

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 6

6. Læg kvadraterne af fejlene sammen. Det sidste trin er at finde summen af værdierne i den tredje kolonne. Det ønskede resultat er SSE eller summen af kvadraterne af fejlene.

For dette datasæt beregnes SSE ved at tilføje de ti værdier i den tredje kolonne:

s s E = 6, 921

${displaystyle SSE=6.921}$

Metode 2 af 3: Opret et Excel-regneark til at beregne SSE

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 7

1. Mærk kolonnerne i regnearket. Du laver en tabel med tre kolonner i Excel, med de samme tre overskrifter som ovenfor.

I celle A1 skal du skrive `Værdi` som overskrift.
I rubrik B1 skal du skrive `Afvigelse` som overskrift.
I rubrik C1 skal du skrive `Afvigelse i kvadrat` som overskrift.

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 8

2. Indtast dine oplysninger. I den første kolonne skal du indtaste værdierne for dine målinger. Hvis sættet er lille, kan du nemt skrive det ind i hånden. Hvis du har et stort datasæt, skal du muligvis kopiere og indsætte dataene i kolonnen.

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 9

3. Bestem gennemsnittet af datapunkterne. Excel har en funktion, der beregner gennemsnittet for dig. I en tom celle under din datatabel (det er lige meget, hvilken celle du vælger), skal du indtaste:

=Gennemsnit(A2:___)

Indtast ikke tom plads. Udfyld dette felt med cellenavnet på dit sidste datapunkt. For eksempel, hvis du har 100 datapunkter, vil du bruge funktionen:

=Gennemsnit(A2:A101)

Denne funktion indeholder data fra cellerne A2 til A101, fordi den øverste række indeholder kolonneoverskrifterne.

Når du trykker på Enter eller klikker til en anden celle i tabellen, udfyldes den nyligt programmerede celle automatisk med gennemsnittet af dine dataværdier.

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 10

4. Gå ind i fejlmålingsfunktionen. I den første tomme celle i kolonnen `Afvigelse` skal du indtaste en funktion til at beregne forskellen mellem hvert datapunkt og middelværdien. For at gøre dette skal du bruge cellenavnet, hvor middelværdien er placeret. Lad os antage, at du har brugt celle A104 for nu.

Fejlberegningsfunktionen, som du indtaster i celle B2, er:

=A2-$A$104. Dollartegnene er nødvendige for at sikre, at du låser boks A104 for hver beregning.

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 11

5. Udfyld funktionen for de kvadratiske fejl. I den tredje kolonne kan du instruere Excel til at beregne det ønskede kvadrat.

Indtast følgende funktion i celle C2:

=B2^2

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 12

6. Kopier funktionerne for at fylde hele tabellen. Efter at have indtastet funktionerne i den øverste celle i hver kolonne, henholdsvis B2 og C2, skal du udfylde hele tabellen. Du kunne skrive funktionen igen i hver linje i tabellen, men det ville tage alt for lang tid. Brug din mus til at markere celler B2 og C2 sammen, og uden at slippe museknappen, træk til den nederste celle i hver kolonne.

Hvis du antager, at du har 100 datapunkter i din tabel, skal du trække musen til cellerne B101 og C101.

Når du slipper museknappen, kopieres formlerne til alle celler i tabellen. Tabellen skal automatisk udfyldes med de beregnede værdier.

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 13

7. Find SSE. Kolonne C i din tabel indeholder alle kvadratiske fejlværdier. Det sidste trin er at lade Excel beregne summen af disse værdier.

Indtast følgende funktion i en celle under tabellen, sandsynligvis C102 i dette eksempel:

=Sum(C2:C101)

Hvis du klikker på Enter eller klikker væk i en anden celle i tabellen, får du SSE-værdien af dine data.

Metode 3 af 3: Relateret SSE til andre statistiske data

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 14

1. Beregn afvigelsen af SSE. At finde SSE for et datasæt er generelt en byggesten til at finde andre, mere nyttige værdier. Den første af disse er varians. Variansen er et mål, der angiver, hvor meget de målte data afviger fra middelværdien. Det er faktisk gennemsnittet af de kvadrerede forskelle fra middelværdien.

Da SSE er summen af de kvadrerede fejl, kan du finde middelværdien (det er variansen) blot ved at dividere med antallet af værdier. Men hvis du beregner variansen af et stikprøvesæt i stedet for en hel population, dividerer du variansen med (n-1) i stedet for n. Så:

Varians = SSE/n, hvis man beregner variansen af en hel population.
Varians = SSE/(n-1), hvis du beregner variansen af en stikprøve af data.

For prøveproblemet med patienternes temperatur kan vi antage, at 10 patienter kun udgør en prøve. Derfor beregnes variansen som følger:

Varians = SSE (n - 1)

${displaystyle {text{Variation}}={frac {text{SSE}}{(n-1)}}}$

Varians = 6, 921 9

${displaystyle {text{Variation}}={frac {6.921}{9}}}$

Varians = 0, 769

${displaystyle {text{Variation}}=0,769}$

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 15

2. Beregn standardafvigelsen for SSE. Standardafvigelsen er en almindeligt anvendt værdi, der angiver, hvor meget værdierne af et datasæt afviger fra middelværdien. Standardafvigelsen er kvadratroden af variansen. Bemærk, at variansen er middelværdien af de kvadrerede fejlmål.

Derfor, efter at du har beregnet SSE, kan du finde standardafvigelsen som følger:

standardafvigelse = \sqrt{SSE} n - 1

${displaystyle {text{Standard Deviation}}={sqrt {frac {text{SSE}}{n-1}}}}$

For prøven af temperaturmålingerne kan du finde standardafvigelsen som følger:

standardafvigelse = \sqrt{SSE} n - 1

${displaystyle {text{Standard Deviation}}={sqrt {frac {text{SSE}}{n-1}}}}$

standardafvigelse = \sqrt{\frac{6,921}{9}}

${displaystyle {text{Standard Deviation}}={sqrt {frac {text{6.921}}{9}}}}$

standardafvigelse = \sqrt{0, 769}

${displaystyle {text{Standard Deviation}}={sqrt {0,769}}}$

standardafvigelse = 0, 877

${displaystyle {text{Standardafvigelse}}=0,877}$

Billede med titlen Beregn summen af kvadrater for fejl (SSE) Trin 16

3. Brug SSE til at bestemme kovariansen. Denne artikel fokuserede på datasæt, der kun måler en enkelt værdi ad gangen. Men i mange undersøgelser kan du sammenligne to separate værdier. For eksempel vil du vide, hvordan disse to værdier relaterer til hinanden, ikke kun til gennemsnittet af datasættet. Denne værdi er kovariansen.

Beregningerne for kovarians er for detaljerede til at blive beskrevet her, bortset fra at du vil bruge SSE for hver datatype og derefter sammenligne den. For en mere detaljeret beskrivelse af kovariansen og de involverede beregninger, se find artikler om dette emne på wikiHow.

Som et eksempel på brug af kovarians kan du sammenligne alderen på patienterne i en medicinsk undersøgelse med effektiviteten af et lægemiddel til at sænke febertemperaturen. Så har du ét datasæt med aldre og et andet datasæt med temperaturer. Du finder så SSE for hvert datasæt, og derfra varians, standardafvigelser og kovarians.