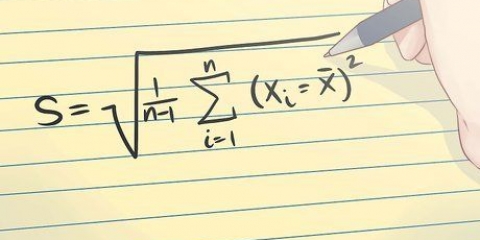I eksemplet med dataindsamling bliver disse afvigelser: 







For at kontrollere gyldigheden af dine beregninger kontrollerer vi, om summen af værdierne i kolonnen med afvigelser er lig med nul. Hvis du lægger alle afvigelser sammen og får noget andet end nul, så er dit gennemsnit forkert, eller du har lavet en fejl i beregningen af en eller flere af afvigelserne. Vend tilbage og tjek dit arbejde. 
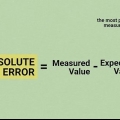
Absolut værdi er et matematisk værktøj til at angive afstand eller størrelse, uanset retning. For at bestemme den absolutte værdi skal du blot udelade minustegnet for hvert tal i den anden kolonne. Så udfyld den tredje kolonne med de absolutte værdier som følger: 









For dette datasæt vil den endelige beregning være: 

For eksempel kan du med dette datasæt sige, at middelværdien er ni og middelafstanden fra middelværdien er 2,75. Bemærk, at nogle værdier er tættere på end 2,75 sammenlignet med andre. Men 2,75 er den gennemsnitlige distance.
Beregning af middelafvigelsen fra middelværdien
Indhold
Når du arbejder med data, er der flere måder at måle, hvor snævert dine dataværdier er grupperet. Det mest almindelige er gennemsnittet. De fleste lærer at beregne middelværdien tidligt i skolen ved at finde summen af en gruppe dataværdier og derefter dividere med antallet af værdier i gruppen. En mere avanceret beregning er den gennemsnitlige afvigelse over middelværdien. Denne beregning fortæller dig, hvor tæt dine værdier er på middelværdien. Du bestemmer dette ved at finde middelværdien af et datasæt, derefter afvigelsen af hver data fra denne middelværdi og derefter middelværdien af disse afvigelser.
Trin
Del 1 af 2: Beregning af gennemsnittet

1. Indsaml og tæl dine data. For ethvert sæt værdier er middelværdien et mål for den centrale værdi. Afhængigt af typen af data vil gennemsnittet give dig den midterste værdi af disse data. For at finde middelværdien skal du først indsamle dine data, enten gennem et eksperiment eller bare givet dem på en opgave.
- Som eksempel bruger vi en given talrække 6, 7, 10, 12, 13, 4, 8 og 12. Denne sekvens er lille nok til at tælle i hånden, og hurtigt se, at det er en sekvens på otte tal.
- Inden for statistikken er variablen
eller
bruges ofte til at angive antallet af værdier i en serie eller samling.

2. Find summen af værdierne. Det første trin i at bestemme middelværdien er at beregne summen af alle værdier. Inden for statistisk notation er hver værdi generelt repræsenteret af variablen  . Summen af alle værdier er givet symbolet
. Summen af alle værdier er givet symbolet  . Det græske store bogstav sigma angiver, at det er summen af værdierne. Beregningen for denne simple serie går sådan her:
. Det græske store bogstav sigma angiver, at det er summen af værdierne. Beregningen for denne simple serie går sådan her:
 . Summen af alle værdier er givet symbolet
. Summen af alle værdier er givet symbolet  . Det græske store bogstav sigma angiver, at det er summen af værdierne. Beregningen for denne simple serie går sådan her:
. Det græske store bogstav sigma angiver, at det er summen af værdierne. Beregningen for denne simple serie går sådan her:

3. Del for at finde gennemsnittet. Til sidst divideres summen med antallet af værdier. Det græske bogstav mu,  , bruges ofte til at angive middelværdien. Beregningen af gennemsnittet forløber derfor som følger:
, bruges ofte til at angive middelværdien. Beregningen af gennemsnittet forløber derfor som følger:
 , bruges ofte til at angive middelværdien. Beregningen af gennemsnittet forløber derfor som følger:
, bruges ofte til at angive middelværdien. Beregningen af gennemsnittet forløber derfor som følger:
Del 2 af 2: Find den gennemsnitlige afvigelse

1. Lav en tabel. For at holde dine data i orden og for at hjælpe med beregningerne er det nyttigt at lave en tabel med tre kolonner. Mærk den første kolonne  . Mærk den anden kolonne
. Mærk den anden kolonne  . Mærk den tredje kolonne
. Mærk den tredje kolonne  .
.
 . Mærk den anden kolonne
. Mærk den anden kolonne  . Mærk den tredje kolonne
. Mærk den tredje kolonne  .
. - Udfyld den første kolonne med værdierne til din beregning.

2. Beregn afvigelsen (afvigelsen) for hver værdi. I anden kolonne, mærket  , angiv afvigelsen eller forskellen mellem hver værdi og middelværdien af serien eller mængden. Find denne værdi ved at trække middelværdien fra hver dataværdi.
, angiv afvigelsen eller forskellen mellem hver værdi og middelværdien af serien eller mængden. Find denne værdi ved at trække middelværdien fra hver dataværdi.
 , angiv afvigelsen eller forskellen mellem hver værdi og middelværdien af serien eller mængden. Find denne værdi ved at trække middelværdien fra hver dataværdi.
, angiv afvigelsen eller forskellen mellem hver værdi og middelværdien af serien eller mængden. Find denne værdi ved at trække middelværdien fra hver dataværdi.








3. Bestem den absolutte værdi af hver afvigelse. Når du beregner hver værdis afvigelse fra middelværdien, vil du kun vide forskellen, ikke om forskellen er positiv eller negativ. Hvad du virkelig har brug for, i matematiske termer, er den absolutte værdi af forskellen. Den absolutte værdi er angivet med lodrette streger| |.










4. Beregn middelværdien af de absolutte afvigelser. Efter at have udfyldt tabellen med tre kolonner, find gennemsnittet af de absolutte værdier i den tredje kolonne. Ligesom du gjorde for at beregne gennemsnittet af startværdierne, skal du lægge afvigelserne sammen og dividere summen med antallet af værdier.


5. Fortolk resultatet. Værdien af middelafvigelsen fra middelværdien er et mål for, hvor tæt værdierne er på hinanden. Dette besvarer spørgsmålet, "Hvor tæt på gennemsnittet er dataværdierne i gennemsnit?"?`
Tips
- Fortsæt med at øve dig, og du vil være i stand til at beregne det uden problemer.
Artikler om emnet "Beregning af middelafvigelsen fra middelværdien"
Оцените, пожалуйста статью
Lignende
Populær