Find den ekstreme værdi af en ligning: 10 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Formlen x = -b/2a
- Metode 2 af 2: Udarbejdelse af ligningen
Tips
Advarsler
Fornødenheder

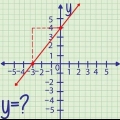
Den ekstreme værdi af en parabel er maksimum eller minimum af ligningen. Hvis du vil finde den ekstreme værdi af en andengradsligning, skal du bruge en formel eller løse ligningen. Her lærer du, hvordan du gør det.

Trin

Metode 1 af 2: Formlen x = -b/2a

1. Bestem værdierne af a, b og c. I en andengrads- eller andengradsligning,x = -en,x = b, og konstanten (leddet uden en variabel) = c. Antag, at vi har at gøre med følgende ligning: y = x + 9x + 18. I dette eksempel, -en = 1, b = 9 og c = 18.

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 2

2. Brug en formel til at finde værdien af x. Parablens toppunkt er også ligningens symmetriakse. Formlen til at finde den ekstreme værdi x af en andengradsligning er x = -b/2a. Udfyld de relevante værdier i denne ligning for at få x at finde. Erstat værdierne med a og b. Sådan gør du:

x=-b/2a

x=-(9)/(2)(1)

x=-9/2

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 3

3. Sæt værdien af x ind i den oprindelige ligning for at få værdien af y. Nu hvor du kender x, er det muligt at anvende denne værdi på den oprindelige ligning for at få y. Formlen til bestemmelse af yderværdien af en andengradsligning er (x, y) = [(-b/2a), f(-b/2a)]. Dette betyder bare, at for at få y, kan du finde x ved at bruge denne formel og derefter sætte den ind i den oprindelige ligning. Sådan går det:

y = x + 9x + 18

y = (-9/2) + 9(-9/2) +18

y = 81/4 -81/2 + 18

y = 81/4 -162/4 + 72/4

y = (81 - 162 + 72)/4

y = -9/4

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 4

4. Skriv værdierne for x og y som et ordnet par. Nu hvor du ved, at x = -9/2 og y = -9/4, skal du bare skrive disse værdier som et ordnet par: (-9/2, -9/4). Den ekstreme værdi af denne andengradsligning er (-9/2, -9/4). Hvis du ville tegne denne parable i en graf, så er dette punkt minimum af parablen, fordi x er positiv.

Metode 2 af 2: Udarbejdelse af ligningen

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 5

1. Skriv ligningen. Udregning af ligningen er en anden måde at finde den ekstreme værdi af en andengradsligning. Med denne metode er det muligt at finde x- og y-koordinaterne med det samme. Lad os sige, at vi arbejder med følgende andengradsligning: x + 4x + 1 = 0.

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 6

2. Divider hvert led med koefficienten x . I dette tilfælde er koefficienten ofx lig med 1, så du kan springe dette trin over. At dividere hvert led med 1 er ligegyldigt!

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 7

3. Flyt konstanten til højre side af ligningen. Konstanten er udtrykket uden koefficient. I dette tilfælde altså "1". Flyt 1-tallet til den anden side af ligningen ved at trække 1 fra begge sider. Sådan gør du det:

x + 4x + 1 = 0

x + 4x + 1 -1 = 0 - 1

x + 4x = - 1

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 8

4. Udfyld firkanten til venstre for ligningen.Arbejde (b/2) og tilføj resultatet til begge sider af ligningen. fylde "4" i som værdi af b, fordi "4x" b-leddet er af ligningen.

(4/2) = 2 = 4. Tilføj nu 4 til begge sider af ligningen for at få følgende:

x + 4x + 4 = -1 + 4

x + 4x + 4 = 3

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 9

5. Faktorer venstre side af ligningen. Nu vil du se, at x + 4x + 4 er et perfekt kvadrat. Dette kan omskrives som (x + 2) = 3

Billede med titlen Find toppunktet for en kvadratisk ligning Trin 10

6. Brug dette til at finde x- og y-koordinaterne. Du kan finde x-koordinaten ved blot at gøre (x + 2) lig med nul. Så hvis (x + 2) = 0, hvad skal x så være? Variablen x skal så være lig med -2 for at kompensere for +2, så x-koordinaten er -2. Y-koordinaten er simpelthen det konstante led på den anden side af ligningen. Så y = 3. Du kan også tage en genvej og tage tallets fortegn i parentes for at finde x-koordinaten. Så ekstremværdien af ligningen x + 4x + 1 = (-2, 3)

Tips

Forstå hvad a, b og c repræsenterer.
Vis dit arbejde og tjek det! Som følge heraf ved din lærer, at du forstår, og du har selv chancen for at se og rette fejl i dine svar.
Overhold denne rækkefølge for behandling for at sikre et godt resultat af opgaven.