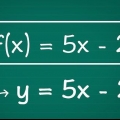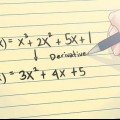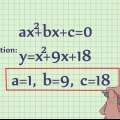Tag eksemplet sammenligning  , hvor y-leddene kan flyttes til venstre ved at trække et y fra begge sider. De øvrige led kan flyttes til højre ved at tilføje 6 på begge sider og
, hvor y-leddene kan flyttes til venstre ved at trække et y fra begge sider. De øvrige led kan flyttes til højre ved at tilføje 6 på begge sider og  at trække af fra begge sider. Den resulterende ligning er
at trække af fra begge sider. Den resulterende ligning er  .
. 
Se eksempelsammenligningen  . Der er ingen begrænsning på de tilladte værdier af x for denne ligning. Du skal dog indse, at dette er ligningen for en parabel, med x=0 som centrum, og en parabel er ikke en funktion, fordi den ikke er en en-til-en sammenligning af x- og y-værdier. For at begrænse denne ligning og gøre den til en funktion, for hvilken vi kan finde en invers, skal vi definere domænet som x≥0.
. Der er ingen begrænsning på de tilladte værdier af x for denne ligning. Du skal dog indse, at dette er ligningen for en parabel, med x=0 som centrum, og en parabel er ikke en funktion, fordi den ikke er en en-til-en sammenligning af x- og y-værdier. For at begrænse denne ligning og gøre den til en funktion, for hvilken vi kan finde en invers, skal vi definere domænet som x≥0. Udvalget er på samme måde begrænset. Bemærk, at den første term,  , vil altid være positiv eller 0 for enhver værdi af x. Så hvis ligningen tilføjer +2, vil området være en hvilken som helst værdi y≥2.
, vil altid være positiv eller 0 for enhver værdi af x. Så hvis ligningen tilføjer +2, vil området være en hvilken som helst værdi y≥2. Det er nødvendigt at definere domænet og omfanget på dette tidlige stadium. Du vil bruge disse definitioner senere, når du definerer domænet og omfanget af den inverse funktion. Faktisk bliver den oprindelige funktions domæne området for den omvendte funktion, og området for den oprindelige funktion bliver domænet for den omvendte funktion. 
Arbejder med eksempelsammenligningen  , dette inversionstrin vil resultere i den nye ligning af
, dette inversionstrin vil resultere i den nye ligning af  .
. Et alternativt format er at erstatte y-leddet med x, men erstatte x-leddet med enten  eller
eller  for at angive den omvendte funktion.
for at angive den omvendte funktion. 
 (oprindelig præmis)
(oprindelig præmis) (træk 2 fra på begge sider)
(træk 2 fra på begge sider) (divider begge sider med 2)
(divider begge sider med 2)± (kvadratrod af begge sider; husk at kvadratroden resulterer i både positive og negative mulige svar)
(kvadratrod af begge sider; husk at kvadratroden resulterer i både positive og negative mulige svar) 
Se løsningen af eksempelligningen ± . Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være
. Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være  altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥2. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥0, hvis du tager den positive løsning af kvadratroden, eller y≤0, hvis du tager den negative løsning af kvadratroden. Bemærk, at for at finde den inverse funktion, definerede du oprindeligt domænet som x≥0. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed.
altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥2. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥0, hvis du tager den positive løsning af kvadratroden, eller y≤0, hvis du tager den negative løsning af kvadratroden. Bemærk, at for at finde den inverse funktion, definerede du oprindeligt domænet som x≥0. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed. Sammenlign domænet og intervallet for det omvendte med domænet og intervallet for originalen. Husk det for den oprindelige funktion,  , domænet blev defineret som alle værdier af x≥0, og området blev defineret som alle værdier af y≥2. For den inverse funktion bytter disse værdier nu, og domænet er alle værdier af x≥2, og området er alle værdier af y≥0.
, domænet blev defineret som alle værdier af x≥0, og området blev defineret som alle værdier af y≥2. For den inverse funktion bytter disse værdier nu, og domænet er alle værdier af x≥2, og området er alle værdier af y≥0. 
Som et eksempel, vælg værdien x=1 for den oprindelige ligning  . Dette giver resultatet y=4.
. Dette giver resultatet y=4. Så sætter du værdien 4 i den inverse funktion  . Dette giver faktisk resultatet y=1. Du kan konkludere, at din inverse funktion er korrekt.
. Dette giver faktisk resultatet y=1. Du kan konkludere, at din inverse funktion er korrekt. 

Bemærk, at denne standardform består af et perfekt kvadratisk udtryk,  , som så modificeres af de to andre elementer a og k. For at nå frem til denne perfekte andengradsform skal du skabe visse betingelser i din andengradsligning.
, som så modificeres af de to andre elementer a og k. For at nå frem til denne perfekte andengradsform skal du skabe visse betingelser i din andengradsligning. 
For at færdiggøre firkanten, arbejd baglæns. Du starter med  og en anden x-termin. Fra koefficienten for det udtryk, som du kan definere som `2b`, skal du få
og en anden x-termin. Fra koefficienten for det udtryk, som du kan definere som `2b`, skal du få  se at finde. Dette kræver en kombination af at dividere med to og derefter kvadrere det resultat.
se at finde. Dette kræver en kombination af at dividere med to og derefter kvadrere det resultat. 
Tag for eksempel den kvadratiske funktion  . Du kan forenkle dette ved at dividere alle led med 2 for at få den resulterende funktion
. Du kan forenkle dette ved at dividere alle led med 2 for at få den resulterende funktion  at få. Koefficienten 2 forbliver uden for parenteserne og vil være en del af din endelige løsning.
at få. Koefficienten 2 forbliver uden for parenteserne og vil være en del af din endelige løsning. Hvis alle led ikke er multipla af a, får du brøkkoefficienter. For eksempel: funktionen  vil blive forenklet til
vil blive forenklet til  . Regn brøkerne omhyggeligt ud.
. Regn brøkerne omhyggeligt ud. 
For eksempel, hvis de to første led i din kvadratiske funktion  du finder det nødvendige tredje led ved at dividere 3 med 2 (eller 3/2) og derefter kvadrere det for at få 9/4. Den kvadratiske
du finder det nødvendige tredje led ved at dividere 3 med 2 (eller 3/2) og derefter kvadrere det for at få 9/4. Den kvadratiske  er en perfekt firkant.
er en perfekt firkant. Et andet eksempel: antag de to første led  er. Halvdelen af mellemleddet er -2, og så kvadrerer du det for at få 4. Den resulterende perfekte firkant er
er. Halvdelen af mellemleddet er -2, og så kvadrerer du det for at få 4. Den resulterende perfekte firkant er  .
. 
Antag at du har funktionen  . Som nævnt ovenfor bruger du de to første led til at fuldføre firkanten. Ved at bruge mellemleddet på -4x genererer du et tredje led +4. Tilføj 4 og træk 4 fra ligningen i formen
. Som nævnt ovenfor bruger du de to første led til at fuldføre firkanten. Ved at bruge mellemleddet på -4x genererer du et tredje led +4. Tilføj 4 og træk 4 fra ligningen i formen  . Parenteserne er kun placeret for at definere den andengradsligning, du laver. Bemærk +4 inde i beslagene og -4 på ydersiden. Forenkle tallene til resultatet
. Parenteserne er kun placeret for at definere den andengradsligning, du laver. Bemærk +4 inde i beslagene og -4 på ydersiden. Forenkle tallene til resultatet  .
. 
Bemærk, at for denne funktion a=1, h=2 og k=5. Værdien af at skrive ligningen på denne form er, at en, fordi den er positiv, fortæller dig, at parablen peger opad. Værdierne (h, k) angiver toppunktet i bunden af parablen, hvis du ville tegne det. 
Fortsæt med at arbejde med preview-funktionen  . Da dette er i standardformat, kan du bestemme toppunktet som x=2, y=5. Så for at undgå symmetrien arbejder du kun med højre side af grafen og indstiller domænet hvis alle værdier x≥2. Indsættelse af værdien x=2 i funktionen returnerer y=5. Du kan se, at værdierne af y vil stige, når x stiger. Derfor er området for denne ligning y≥5.
. Da dette er i standardformat, kan du bestemme toppunktet som x=2, y=5. Så for at undgå symmetrien arbejder du kun med højre side af grafen og indstiller domænet hvis alle værdier x≥2. Indsættelse af værdien x=2 i funktionen returnerer y=5. Du kan se, at værdierne af y vil stige, når x stiger. Derfor er området for denne ligning y≥5. 
Fortsæt med at arbejde med funktionen  . Indsæt x i stedet for f(x), og indsæt y (eller f(x), hvis du foretrækker det) i stedet for x. Dette giver som en ny funktion
. Indsæt x i stedet for f(x), og indsæt y (eller f(x), hvis du foretrækker det) i stedet for x. Dette giver som en ny funktion  .
. 
 (oprindeligt udgangspunkt)
(oprindeligt udgangspunkt) (træk 5 fra begge sider)
(træk 5 fra begge sider)± (kvadratrod af begge sider; husk at kvadratroden giver både positive og negative mulige svar)
(kvadratrod af begge sider; husk at kvadratroden giver både positive og negative mulige svar) ± (tilføj 2 til begge sider)
(tilføj 2 til begge sider) 
Se løsningen af eksempelligningen ± . Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være
. Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være  altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥5. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥2 (hvis du tager den positive løsning af kvadratroden), eller y≤2 (hvis du vælger den negative løsning af kvadratroden). Husk, at du oprindeligt definerede domænet som x≥2, for at finde den inverse funktion. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed.
altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥5. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥2 (hvis du tager den positive løsning af kvadratroden), eller y≤2 (hvis du vælger den negative løsning af kvadratroden). Husk, at du oprindeligt definerede domænet som x≥2, for at finde den inverse funktion. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed. Sammenlign domænet og intervallet for det omvendte med domænet og intervallet for originalen. Husk på, at for den oprindelige funktion var domænet defineret som alle værdier af x≥2, og området blev defineret som alle værdier af y≥5. For denne inverse funktion bytter disse værdier, og domænet er nu alle værdier af x≥5, og området er alle værdier af y≥2. 
Som et eksempel, vælg værdien x=3, der skal inkluderes i den oprindelige ligning  at behandle. Dette giver resultatet y=6.
at behandle. Dette giver resultatet y=6. Så behandler du y=6 i den inverse funktion  . Dette returnerer y=3, som er det tal, du startede med. Du kan konkludere, at din inverse funktion er korrekt.
. Dette returnerer y=3, som er det tal, du startede med. Du kan konkludere, at din inverse funktion er korrekt. 

Til dette afsnit af denne artikel skal du bruge eksempelligningen  .
. 

Baseret på arbejdsligningen  , giver dette resultatet
, giver dette resultatet  .
. 
Til eksempelligningen skal du trække x fra begge sider af ligningen for at få venstre side lig med nul. Dette giver resultatet  .
. 
Forlade  . Altså x=1
. Altså x=1 Forlade  . Så b=2
. Så b=2 Forlade  . Så c=(-3-x)
. Så c=(-3-x) 
x=[-b±√(b^2-4ac)]/2a x=(-2)±√((-2)^2-4(1)(-3-x)) / 2(1) x=((-2)±√(4+12+4x)))/2 x=(-2±√(16+4x))/2 x=(-2±√(4)(4+x)))/2 x=-2±2√(4+x))/2 x=-1±√(4+x) f-invers = -1±√(4+x)(Dette sidste trin er muligt, fordi du byttede f(x) til variablen x på et tidligere tidspunkt). 




Forudsat den oprindelige funktion  , vælg din x=-2. Dette returnerer y=-3. Erstat nu værdien af x=-3 i den inverse funktion,
, vælg din x=-2. Dette returnerer y=-3. Erstat nu værdien af x=-3 i den inverse funktion,  . Dette returnerer -2, hvilket faktisk er den værdi, du startede med. Så din definition af den inverse funktion er korrekt.
. Dette returnerer -2, hvilket faktisk er den værdi, du startede med. Så din definition af den inverse funktion er korrekt.
Find det omvendte af en andengradsligning
Indhold
Inverse funktioner kan være meget nyttige til at løse mange matematiske problemer. At kunne tage en funktion og finde dens omvendte funktion er et stærkt værktøj. Men med andengradsligninger kan dette være en ret kompliceret proces. Først skal du omhyggeligt definere ligningen ved at bestemme et passende domæne og område. Du kan derefter vælge mellem tre metoder til at beregne den inverse funktion. Valget af metode er primært et spørgsmål om personlig præference.
Trin
Metode 1 af 3: Find det omvendte af en simpel funktion

1. Find en funktion i form af y = -en x 2 + c  . Hvis du har den `rigtige` slags funktion til at starte med, kan du finde det omvendte med en simpel algebra. Denne form er en slags variation på
. Hvis du har den `rigtige` slags funktion til at starte med, kan du finde det omvendte med en simpel algebra. Denne form er en slags variation på  . Hvis du sammenligner dette med en standard kvadratisk funktion,
. Hvis du sammenligner dette med en standard kvadratisk funktion,  , se, at mellemlang sigt
, se, at mellemlang sigt  mangler. En anden måde at sige dette på er, at værdien af b er nul. Hvis din funktion har denne form, er det ret nemt at finde det omvendte.
mangler. En anden måde at sige dette på er, at værdien af b er nul. Hvis din funktion har denne form, er det ret nemt at finde det omvendte.
 . Hvis du har den `rigtige` slags funktion til at starte med, kan du finde det omvendte med en simpel algebra. Denne form er en slags variation på
. Hvis du har den `rigtige` slags funktion til at starte med, kan du finde det omvendte med en simpel algebra. Denne form er en slags variation på  . Hvis du sammenligner dette med en standard kvadratisk funktion,
. Hvis du sammenligner dette med en standard kvadratisk funktion,  , se, at mellemlang sigt
, se, at mellemlang sigt  mangler. En anden måde at sige dette på er, at værdien af b er nul. Hvis din funktion har denne form, er det ret nemt at finde det omvendte.
mangler. En anden måde at sige dette på er, at værdien af b er nul. Hvis din funktion har denne form, er det ret nemt at finde det omvendte. - Din oprindelige funktion behøver ikke at ligne nøjagtigt
. Så længe du kan se på det og se, at funktionen kun består af
led og konstante tal, vil du kunne bruge denne metode.
- Antag, at du starter med ligningen
. En hurtig undersøgelse af denne ligning afslører, at der ikke er nogen vilkår for
at være til den første magt. Denne ligning er en kandidat til denne metode til at finde en invers funktion.

2. Forenkle ved at kombinere ens udtryk. Den indledende ligning kan have flere led i en kombination af addition og subtraktion. Dit første skridt er at kombinere lignende udtryk for at forenkle ligningen og omskrive den i standardformatet  .
.
 .
. , hvor y-leddene kan flyttes til venstre ved at trække et y fra begge sider. De øvrige led kan flyttes til højre ved at tilføje 6 på begge sider og
, hvor y-leddene kan flyttes til venstre ved at trække et y fra begge sider. De øvrige led kan flyttes til højre ved at tilføje 6 på begge sider og  at trække af fra begge sider. Den resulterende ligning er
at trække af fra begge sider. Den resulterende ligning er  .
.
3. Bestem den forenklede funktions domæne og rækkevidde. Husk, at domænet af en funktion består af de mulige værdier af x, der kan anvendes til at give en reel løsning. Området for en funktion består af værdierne af y, der vil returnere. For at bestemme funktionens domæne skal du kigge efter værdier, der giver et matematisk umuligt resultat. Du angiver derefter domænet, hvis alle andre værdier af x. For at finde intervallet skal du overveje værdierne af y ved vilkårlige grænsepunkter og se på funktionens opførsel.
 . Der er ingen begrænsning på de tilladte værdier af x for denne ligning. Du skal dog indse, at dette er ligningen for en parabel, med x=0 som centrum, og en parabel er ikke en funktion, fordi den ikke er en en-til-en sammenligning af x- og y-værdier. For at begrænse denne ligning og gøre den til en funktion, for hvilken vi kan finde en invers, skal vi definere domænet som x≥0.
. Der er ingen begrænsning på de tilladte værdier af x for denne ligning. Du skal dog indse, at dette er ligningen for en parabel, med x=0 som centrum, og en parabel er ikke en funktion, fordi den ikke er en en-til-en sammenligning af x- og y-værdier. For at begrænse denne ligning og gøre den til en funktion, for hvilken vi kan finde en invers, skal vi definere domænet som x≥0. , vil altid være positiv eller 0 for enhver værdi af x. Så hvis ligningen tilføjer +2, vil området være en hvilken som helst værdi y≥2.
, vil altid være positiv eller 0 for enhver værdi af x. Så hvis ligningen tilføjer +2, vil området være en hvilken som helst værdi y≥2.
4. Byt rollerne for x- og y-leddet. Uden at ændre ligningen på anden måde, skal du erstatte alle former af y med x, og alle former af x med y. Dette er det trin, der faktisk `inverterer` ligningen.
 , dette inversionstrin vil resultere i den nye ligning af
, dette inversionstrin vil resultere i den nye ligning af  .
. eller
eller  for at angive den omvendte funktion.
for at angive den omvendte funktion.
5. Omskriv den omvendte ligning i form af y. Ved at bruge en kombination af algebraiske trin og sikre, at den samme operation udføres på begge sider af ligningen, bliver du nødt til at isolere variablen y. Til sammenligningen  , denne revision ser sådan ud:
, denne revision ser sådan ud:
 , denne revision ser sådan ud:
, denne revision ser sådan ud: (oprindelig præmis)
(oprindelig præmis) (træk 2 fra på begge sider)
(træk 2 fra på begge sider) (divider begge sider med 2)
(divider begge sider med 2) (kvadratrod af begge sider; husk at kvadratroden resulterer i både positive og negative mulige svar)
(kvadratrod af begge sider; husk at kvadratroden resulterer i både positive og negative mulige svar)
6. Bestem domænet og området for den inverse funktion. Som i begyndelsen skal du undersøge den omvendte ligning for at bestemme domænet og området. Med to mulige løsninger skal du vælge den løsning, der har et domæne og område, der er det omvendte af det oprindelige domæne og område.
 . Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være
. Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være  altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥2. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥0, hvis du tager den positive løsning af kvadratroden, eller y≤0, hvis du tager den negative løsning af kvadratroden. Bemærk, at for at finde den inverse funktion, definerede du oprindeligt domænet som x≥0. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed.
altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥2. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥0, hvis du tager den positive løsning af kvadratroden, eller y≤0, hvis du tager den negative løsning af kvadratroden. Bemærk, at for at finde den inverse funktion, definerede du oprindeligt domænet som x≥0. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed. , domænet blev defineret som alle værdier af x≥0, og området blev defineret som alle værdier af y≥2. For den inverse funktion bytter disse værdier nu, og domænet er alle værdier af x≥2, og området er alle værdier af y≥0.
, domænet blev defineret som alle værdier af x≥0, og området blev defineret som alle værdier af y≥2. For den inverse funktion bytter disse værdier nu, og domænet er alle værdier af x≥2, og området er alle værdier af y≥0.
7. Tjek om din omvendte funktion virker. For at sikre, at dit arbejde er korrekt, og din inverse er den rigtige ligning, skal du vælge en værdi for x og placere den i den oprindelige ligning for at finde y. Sæt derefter værdien af y i stedet for x i din omvendte ligning, og se om du får det tal, du startede med. Hvis ja, er din omvendte funktion korrekt.
 . Dette giver resultatet y=4.
. Dette giver resultatet y=4. . Dette giver faktisk resultatet y=1. Du kan konkludere, at din inverse funktion er korrekt.
. Dette giver faktisk resultatet y=1. Du kan konkludere, at din inverse funktion er korrekt.Metode 2 af 3: Udfyld kvadratet for at finde den inverse funktion

1. Giv andengradsligningen den rigtige form. For at finde det omvendte skal du starte med formens ligning  . Hvis det er nødvendigt, skal du kombinere lignende udtryk for at få ligningen i dette format. Med ligningen skrevet på denne måde, kan du fortælle lidt mere om den.
. Hvis det er nødvendigt, skal du kombinere lignende udtryk for at få ligningen i dette format. Med ligningen skrevet på denne måde, kan du fortælle lidt mere om den.
 . Hvis det er nødvendigt, skal du kombinere lignende udtryk for at få ligningen i dette format. Med ligningen skrevet på denne måde, kan du fortælle lidt mere om den.
. Hvis det er nødvendigt, skal du kombinere lignende udtryk for at få ligningen i dette format. Med ligningen skrevet på denne måde, kan du fortælle lidt mere om den. - Det første du vil bemærke er værdien af koefficienten a. hvis en>0, så definerer ligningen en parabel, hvis ender peger opad (dalparabel). hvis en<0, så definerer ligningen en parabel, hvis ender peger nedad (bjergparabel). Bemærk, at a≠0. Hvis det ikke var, ville dette være en lineær funktion og ikke en kvadratisk.

2. Genkend standardformatet for kvadratisk. Før du kan finde den inverse funktion, skal du omskrive ligningen i standardformatet. Standardformatet for en kvadratisk funktion er  . De numeriske led a, h og k vil blive evalueret, hvis du transformerer ligningen ved at beregne kvadratet.
. De numeriske led a, h og k vil blive evalueret, hvis du transformerer ligningen ved at beregne kvadratet.
 . De numeriske led a, h og k vil blive evalueret, hvis du transformerer ligningen ved at beregne kvadratet.
. De numeriske led a, h og k vil blive evalueret, hvis du transformerer ligningen ved at beregne kvadratet. , som så modificeres af de to andre elementer a og k. For at nå frem til denne perfekte andengradsform skal du skabe visse betingelser i din andengradsligning.
, som så modificeres af de to andre elementer a og k. For at nå frem til denne perfekte andengradsform skal du skabe visse betingelser i din andengradsligning.
3. Tænk tilbage på formen af en perfekt kvadratisk funktion. Husk på, at en andengradsfunktion, der er et perfekt kvadrat, opstår fra to binomialer af  , eller
, eller  . Hvis du gør denne multiplikation, får du
. Hvis du gør denne multiplikation, får du  . Så det første led i andengraden er det første led i binomialet, i anden kvadrat, og det sidste led i andengraden er kvadratet af det andet led i binomialet. Mellemleddet består af to gange produktet af de to led, i dette tilfælde
. Så det første led i andengraden er det første led i binomialet, i anden kvadrat, og det sidste led i andengraden er kvadratet af det andet led i binomialet. Mellemleddet består af to gange produktet af de to led, i dette tilfælde  .
.
 , eller
, eller  . Hvis du gør denne multiplikation, får du
. Hvis du gør denne multiplikation, får du  . Så det første led i andengraden er det første led i binomialet, i anden kvadrat, og det sidste led i andengraden er kvadratet af det andet led i binomialet. Mellemleddet består af to gange produktet af de to led, i dette tilfælde
. Så det første led i andengraden er det første led i binomialet, i anden kvadrat, og det sidste led i andengraden er kvadratet af det andet led i binomialet. Mellemleddet består af to gange produktet af de to led, i dette tilfælde  .
. og en anden x-termin. Fra koefficienten for det udtryk, som du kan definere som `2b`, skal du få
og en anden x-termin. Fra koefficienten for det udtryk, som du kan definere som `2b`, skal du få  se at finde. Dette kræver en kombination af at dividere med to og derefter kvadrere det resultat.
se at finde. Dette kræver en kombination af at dividere med to og derefter kvadrere det resultat.
4. Sørg for, at koefficienten på x 2  1 er. Kan du huske den oprindelige form af den kvadratiske funktion
1 er. Kan du huske den oprindelige form af den kvadratiske funktion  . Hvis den første koefficient er noget andet end 1, skal du dividere alle led med denne værdi for at få a=1.
. Hvis den første koefficient er noget andet end 1, skal du dividere alle led med denne værdi for at få a=1.
 1 er. Kan du huske den oprindelige form af den kvadratiske funktion
1 er. Kan du huske den oprindelige form af den kvadratiske funktion  . Hvis den første koefficient er noget andet end 1, skal du dividere alle led med denne værdi for at få a=1.
. Hvis den første koefficient er noget andet end 1, skal du dividere alle led med denne værdi for at få a=1. . Du kan forenkle dette ved at dividere alle led med 2 for at få den resulterende funktion
. Du kan forenkle dette ved at dividere alle led med 2 for at få den resulterende funktion  at få. Koefficienten 2 forbliver uden for parenteserne og vil være en del af din endelige løsning.
at få. Koefficienten 2 forbliver uden for parenteserne og vil være en del af din endelige løsning. vil blive forenklet til
vil blive forenklet til  . Regn brøkerne omhyggeligt ud.
. Regn brøkerne omhyggeligt ud.
5. Find halvdelen af den midterste koefficient og firkant den. Du har allerede de to første led i den kvadratiske formel. Disse er udtrykket  og koefficienten, der repræsenterer x-leddet. Ved at tage denne koefficient som den værdi, den har, kan du tilføje eller trække det tal, der er nødvendigt for at lave et perfekt kvadrat. Husk ovenfra, at det krævede tredje led i kvadratet er denne anden koefficient divideret med to og derefter i anden.
og koefficienten, der repræsenterer x-leddet. Ved at tage denne koefficient som den værdi, den har, kan du tilføje eller trække det tal, der er nødvendigt for at lave et perfekt kvadrat. Husk ovenfra, at det krævede tredje led i kvadratet er denne anden koefficient divideret med to og derefter i anden.
 og koefficienten, der repræsenterer x-leddet. Ved at tage denne koefficient som den værdi, den har, kan du tilføje eller trække det tal, der er nødvendigt for at lave et perfekt kvadrat. Husk ovenfra, at det krævede tredje led i kvadratet er denne anden koefficient divideret med to og derefter i anden.
og koefficienten, der repræsenterer x-leddet. Ved at tage denne koefficient som den værdi, den har, kan du tilføje eller trække det tal, der er nødvendigt for at lave et perfekt kvadrat. Husk ovenfra, at det krævede tredje led i kvadratet er denne anden koefficient divideret med to og derefter i anden. du finder det nødvendige tredje led ved at dividere 3 med 2 (eller 3/2) og derefter kvadrere det for at få 9/4. Den kvadratiske
du finder det nødvendige tredje led ved at dividere 3 med 2 (eller 3/2) og derefter kvadrere det for at få 9/4. Den kvadratiske  er en perfekt firkant.
er en perfekt firkant. er. Halvdelen af mellemleddet er -2, og så kvadrerer du det for at få 4. Den resulterende perfekte firkant er
er. Halvdelen af mellemleddet er -2, og så kvadrerer du det for at få 4. Den resulterende perfekte firkant er  .
.
6. Tilføj og træk fra den påkrævede tredje term på samme tid. Dette er et vanskeligt koncept, men det virker. Tilføjelse og subtrahering af det samme tal forskellige steder i din funktion ændrer ikke rigtigt værdien af funktionen. Men ved at gøre dette får du din funktion i ordentlig form.
 . Som nævnt ovenfor bruger du de to første led til at fuldføre firkanten. Ved at bruge mellemleddet på -4x genererer du et tredje led +4. Tilføj 4 og træk 4 fra ligningen i formen
. Som nævnt ovenfor bruger du de to første led til at fuldføre firkanten. Ved at bruge mellemleddet på -4x genererer du et tredje led +4. Tilføj 4 og træk 4 fra ligningen i formen  . Parenteserne er kun placeret for at definere den andengradsligning, du laver. Bemærk +4 inde i beslagene og -4 på ydersiden. Forenkle tallene til resultatet
. Parenteserne er kun placeret for at definere den andengradsligning, du laver. Bemærk +4 inde i beslagene og -4 på ydersiden. Forenkle tallene til resultatet  .
.
7. Faktorer den andengradsligning. Polynomiet i parentes er en andengradsligning, som du kan omskrive som  . I eksemplet fra forrige trin (
. I eksemplet fra forrige trin ( ) du indregner den kvadratiske faktor
) du indregner den kvadratiske faktor  . Kopier resten af ligningen, så din løsning
. Kopier resten af ligningen, så din løsning  er ved at blive. Dette er den samme funktion som din oprindelige andengradsligning (
er ved at blive. Dette er den samme funktion som din oprindelige andengradsligning ( ), omskrevet som standardformularen
), omskrevet som standardformularen  .
.
 . I eksemplet fra forrige trin (
. I eksemplet fra forrige trin ( ) du indregner den kvadratiske faktor
) du indregner den kvadratiske faktor  . Kopier resten af ligningen, så din løsning
. Kopier resten af ligningen, så din løsning  er ved at blive. Dette er den samme funktion som din oprindelige andengradsligning (
er ved at blive. Dette er den samme funktion som din oprindelige andengradsligning ( ), omskrevet som standardformularen
), omskrevet som standardformularen  .
.
8. Definer funktionens domæne og omfang. Domænet er det sæt af x-værdier, der kan bruges som input til funktionen. Området er det sæt af y-værdier, der kan være resultatet. Husk på, at en parabel ikke er en funktion med en definerbar invers, fordi der ikke er nogen en-til-en sammenhæng mellem x-værdier og y-værdier på grund af parablens symmetri. For at løse dette problem skal du definere domænet som alle værdier af x, der er større end x=h, parablens toppunkt.
 . Da dette er i standardformat, kan du bestemme toppunktet som x=2, y=5. Så for at undgå symmetrien arbejder du kun med højre side af grafen og indstiller domænet hvis alle værdier x≥2. Indsættelse af værdien x=2 i funktionen returnerer y=5. Du kan se, at værdierne af y vil stige, når x stiger. Derfor er området for denne ligning y≥5.
. Da dette er i standardformat, kan du bestemme toppunktet som x=2, y=5. Så for at undgå symmetrien arbejder du kun med højre side af grafen og indstiller domænet hvis alle værdier x≥2. Indsættelse af værdien x=2 i funktionen returnerer y=5. Du kan se, at værdierne af y vil stige, når x stiger. Derfor er området for denne ligning y≥5.
9. Skift x- og y-værdierne. Dette er det trin, hvor du starter med at finde den omvendte form af ligningen. Lad ligningen være i sin helhed undtagen at bytte disse variable.
 . Indsæt x i stedet for f(x), og indsæt y (eller f(x), hvis du foretrækker det) i stedet for x. Dette giver som en ny funktion
. Indsæt x i stedet for f(x), og indsæt y (eller f(x), hvis du foretrækker det) i stedet for x. Dette giver som en ny funktion  .
.
10. Omskriv den omvendte ligning i form af y. Brug en kombination af algebraiske trin, og sørg for at udføre den samme operation jævnt på begge sider af ligningen, isoler variablen y. Til arbejdssammenligningen  denne revision ser sådan ud:
denne revision ser sådan ud:
 denne revision ser sådan ud:
denne revision ser sådan ud: (oprindeligt udgangspunkt)
(oprindeligt udgangspunkt) (træk 5 fra begge sider)
(træk 5 fra begge sider) (kvadratrod af begge sider; husk at kvadratroden giver både positive og negative mulige svar)
(kvadratrod af begge sider; husk at kvadratroden giver både positive og negative mulige svar) (tilføj 2 til begge sider)
(tilføj 2 til begge sider)
11. Bestem domænet og området for den inverse funktion. Som i begyndelsen skal du undersøge den omvendte ligning for at bestemme domænet og området. Med to mulige løsninger skal du vælge den løsning, der har et domæne og område, der er det omvendte af det oprindelige domæne og område.
 . Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være
. Da kvadratrodsfunktionen ikke er defineret for negative værdier, skal udtrykket . være  altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥5. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥2 (hvis du tager den positive løsning af kvadratroden), eller y≤2 (hvis du vælger den negative løsning af kvadratroden). Husk, at du oprindeligt definerede domænet som x≥2, for at finde den inverse funktion. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed.
altid være positiv. Derfor skal de tilladte værdier for x (domænet) være x≥5. Med det som domæne er de resulterende værdier af y (området) enten alle værdier y≥2 (hvis du tager den positive løsning af kvadratroden), eller y≤2 (hvis du vælger den negative løsning af kvadratroden). Husk, at du oprindeligt definerede domænet som x≥2, for at finde den inverse funktion. Derfor er den korrekte løsning for den omvendte funktion den positive mulighed.
12. Tjek om din omvendte funktion virker. For at sikre, at dit arbejde er korrekt, og din inverse er den rigtige ligning, skal du vælge en værdi for x og placere den i den oprindelige ligning for at finde y. Sæt derefter værdien af y i stedet for x i din omvendte ligning, og se om du får det tal, du startede med. Hvis ja, så er din omvendte funktion korrekt.
 at behandle. Dette giver resultatet y=6.
at behandle. Dette giver resultatet y=6. . Dette returnerer y=3, som er det tal, du startede med. Du kan konkludere, at din inverse funktion er korrekt.
. Dette returnerer y=3, som er det tal, du startede med. Du kan konkludere, at din inverse funktion er korrekt.Metode 3 af 3: Brug af kvadratformlen

1. Brug den kvadratiske formel til at løse x. Husk, når du løser andengradsligninger, er der én metode til at faktorisere dem (hvis det er muligt). Hvis factoring ikke virkede, kunne du bruge kvadratformlen, som ville give de rigtige løsninger til enhver andengradsligning. Du kan også bruge kvadratformlen som en metode til at finde inverse funktioner.
- Kvadratformlen er x=[-b±√(b^2-4ac)]/2a.
- Bemærk, at kvadratformlen giver to mulige løsninger, en positiv og en negativ. Du træffer dette valg baseret på at bestemme funktionens domæne og omfang.

2. Start med en andengradsligning for at finde det omvendte. Din andengradsligning skal starte i formatet  . Tag de algebraiske trin, der er nødvendige for at få din ligning i den form.
. Tag de algebraiske trin, der er nødvendige for at få din ligning i den form.
 . Tag de algebraiske trin, der er nødvendige for at få din ligning i den form.
. Tag de algebraiske trin, der er nødvendige for at få din ligning i den form. .
.
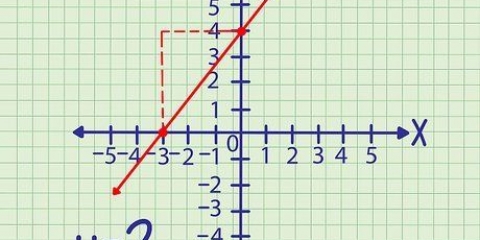
3. Plot ligningen for at bestemme domænet og området. Tegn grafen til funktionen, enten ved hjælp af en grafregner eller plot flere punkter, indtil du kan tegne parablen. Du vil se, at denne ligning definerer en parabel med det højeste punkt ved (-1,-4). Så for at definere dette som en funktion, der vil have en invers, definerer du domænet som alle værdier af x≤-1. Området er så alle værdier y≥-4.

4. Skift variablerne x og y. For at finde den inverse, skift variablerne x og y. Lad ligningen være uændret, undtagen skift variablerne. På dette stadium skal du erstatte x med f(x).
 , giver dette resultatet
, giver dette resultatet  .
.
5. Indstil venstre side af ligningen lig med nul. Husk at for at bruge andengradsformlen skal du sætte ligningen lig med nul, og derefter bruge koefficienterne i formlen. På samme måde starter denne metode til at finde en invers funktion med at sætte ligningen lig nul.
 .
.
6. Omdefiner variablerne, så de passer til kvadratformlen. Dette trin er lidt tricky. Vid, at kvadratformlen løser for x i ligningen  . Så for den ligning du har nu,
. Så for den ligning du har nu,  , for at overholde denne klassifikation skal du omdefinere termerne som følger:
, for at overholde denne klassifikation skal du omdefinere termerne som følger:
 . Så for den ligning du har nu,
. Så for den ligning du har nu,  , for at overholde denne klassifikation skal du omdefinere termerne som følger:
, for at overholde denne klassifikation skal du omdefinere termerne som følger: . Altså x=1
. Altså x=1 . Så b=2
. Så b=2 . Så c=(-3-x)
. Så c=(-3-x)
7. Løs kvadratformlen med disse omdefinerede værdier. Normalt vil du behandle værdierne af a, b og c i kvadratformlen for at løse for x. Husk dog, at du tidligere byttede x og y for at finde den omvendte funktion. Så når du bruger kvadratformlen til at løse for x, løser du faktisk y eller f-inverse. Trinene til løsning af kvadratformlen fungerer som følger:

8. Skriv de to mulige løsninger ned. Bemærk, at kvadratformlen giver to mulige udfald ved at bruge symbolet ±. Skriv de to separate løsninger ud for at gøre det nemmere at bestemme domæne og rækkevidde og give den rigtige endelige løsning. Disse to løsninger er:



9. Bestem domænet og området for den inverse funktion. Bemærk, at for at definere kvadratroden skal domænet være x≥-4. Husk, at domænet for den oprindelige funktion var x≤-1 og området var y≥-4. For at vælge den inverse funktion, der svarer, har du brug for den anden løsning,  vælge som den korrekte inverse funktion.
vælge som den korrekte inverse funktion.
 vælge som den korrekte inverse funktion.
vælge som den korrekte inverse funktion.
10. Tjek om din omvendte funktion er korrekt. For at sikre, at dit arbejde er korrekt, og din inverse er den rigtige ligning, skal du vælge en værdi for x og sætte den i den oprindelige ligning for at finde y. Sæt derefter værdien af y i stedet for x i din omvendte ligning, og se om du får det tal, du startede med. Hvis ja, så er din omvendte funktion korrekt.
 , vælg din x=-2. Dette returnerer y=-3. Erstat nu værdien af x=-3 i den inverse funktion,
, vælg din x=-2. Dette returnerer y=-3. Erstat nu værdien af x=-3 i den inverse funktion,  . Dette returnerer -2, hvilket faktisk er den værdi, du startede med. Så din definition af den inverse funktion er korrekt.
. Dette returnerer -2, hvilket faktisk er den værdi, du startede med. Så din definition af den inverse funktion er korrekt.Artikler om emnet "Find det omvendte af en andengradsligning"
Оцените, пожалуйста статью
Populær