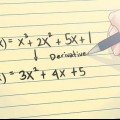(Skriv den oprindelige funktion ned.)
(Skriv den oprindelige funktion ned.) (Omskriv roden som en eksponent.)
(Omskriv roden som en eksponent.) (Find den afledede ved hjælp af potensreglen.)
(Find den afledede ved hjælp af potensreglen.) (Forenkle eksponenten.)
(Forenkle eksponenten.)
Fortsætter man med kvadratroden af funktionen x ovenfra, kan den afledede forenkles som følger: 




For eksempel: antag, at du har den afledte af  ønsker at finde. Definer derefter de to dele som følger:
ønsker at finde. Definer derefter de to dele som følger: 





Bestem derefter den afledede af den anden funktion: 







I funktionen  , er rodnummeret
, er rodnummeret  . Den afledte er
. Den afledte er  .
. I funktionen  , er rodnummeret
, er rodnummeret  . Den afledte er
. Den afledte er  .
. I funktionen  , er rodnummeret
, er rodnummeret  . Den afledte er
. Den afledte er  .
. 
hvis  , derefter
, derefter 
hvis  , derefter
, derefter 
hvis  , derefter
, derefter 

hvis  , derefter
, derefter 
hvis  , derefter
, derefter 
hvis  , derefter
, derefter 

hvis  , derefter
, derefter 
hvis  , derefter
, derefter 
hvis  , derefter
, derefter 
Find den afledede af kvadratroden af x
Indhold
Hvis du tog matematik i skolen, skal du have lært potensreglen til at bestemme den afledede af simple funktioner. Men når funktionen indeholder en kvadratrod eller radikal, som f.eks 
Trin
Metode 1 af 3: Anvendelse af magtreglen

1. Se igen på magtreglen for derivater. Den første regel, du sikkert har lært for at finde derivater, er magtens regel. Denne regel siger det for en variabel  i magten af et tal
i magten af et tal  , er den afledte og beregnes som følger:
, er den afledte og beregnes som følger:
 i magten af et tal
i magten af et tal  , er den afledte og beregnes som følger:
, er den afledte og beregnes som følger: - Tag et kig på følgende eksempelfunktioner og deres derivater:
- hvis
, derefter
- hvis
, derefter
- hvis
, derefter
- hvis
, derefter

2. Omskriv kvadratroden som eksponent. For at finde den afledede af en kvadratrodsfunktion skal du huske, at kvadratroden af et tal eller en variabel også kan skrives som en eksponent. Udtrykket under radikalet er skrevet som en base, og hæves til magten 1/2. Udtrykket bruges også som eksponent for kvadratroden. Se følgende eksempler igennem:




3. Anvend magtens regel. Hvis funktionen er den enkleste kvadratrod,  , Anvend derefter potensreglen som følger for at finde den afledede:
, Anvend derefter potensreglen som følger for at finde den afledede:
 , Anvend derefter potensreglen som følger for at finde den afledede:
, Anvend derefter potensreglen som følger for at finde den afledede: (Skriv den oprindelige funktion ned.)
(Skriv den oprindelige funktion ned.) (Omskriv roden som en eksponent.)
(Omskriv roden som en eksponent.) (Find den afledede ved hjælp af potensreglen.)
(Find den afledede ved hjælp af potensreglen.) (Forenkle eksponenten.)
(Forenkle eksponenten.)
4. Forenkle resultatet. På dette stadium skal du vide, at en negativ eksponent betyder, at du tager det omvendte af, hvad der ville være tallet med den positive eksponent. Eksponenten for  betyder, at kvadratroden af grundfladen bliver nævneren af en brøk.
betyder, at kvadratroden af grundfladen bliver nævneren af en brøk.
 betyder, at kvadratroden af grundfladen bliver nævneren af en brøk.
betyder, at kvadratroden af grundfladen bliver nævneren af en brøk.


Metode 2 af 3: Anvendelse af kædereglen for kvadratrodsfunktioner

1. Revider kædereglen for funktioner. Kædereglen er en regel for afledte værdier, som du bruger, når den oprindelige funktion kombinerer en funktion i en anden funktion. Det siger kædereglen for to funktioner  og
og  , den afledte af kombinationen af de to funktioner kan findes som følger:
, den afledte af kombinationen af de to funktioner kan findes som følger:
 og
og  , den afledte af kombinationen af de to funktioner kan findes som følger:
, den afledte af kombinationen af de to funktioner kan findes som følger: - hvis
, derefter
.

2. Definer kæderegelfunktionerne. Brug af kædereglen kræver, at du først definerer de to funktioner, der udgør din kombinerede funktion. For kvadratrodsfunktioner er den yderste funktion  kvadratrodsfunktionen og den inderste funktion
kvadratrodsfunktionen og den inderste funktion  funktionen under det radikale.
funktionen under det radikale.
 kvadratrodsfunktionen og den inderste funktion
kvadratrodsfunktionen og den inderste funktion  funktionen under det radikale.
funktionen under det radikale. ønsker at finde. Definer derefter de to dele som følger:
ønsker at finde. Definer derefter de to dele som følger:


3. Find de afledte funktioner af de to funktioner. For at anvende kædereglen på kvadratroden af en funktion, skal du først finde den afledede af den generelle kvadratrodsfunktion:






4. Kombiner funktionerne i kædereglen. Kædereglen er  . Kombiner derivaterne som følger:
. Kombiner derivaterne som følger:
 . Kombiner derivaterne som følger:
. Kombiner derivaterne som følger:


Metode 3 af 3: Find hurtigt de afledte rodfunktioner

1. Bestem afledte af en kvadratrodsfunktion ved hjælp af en hurtig metode. Når du vil finde den afledede af kvadratroden af en variabel eller en funktion, kan du anvende en simpel regel: Den afledede vil altid være den afledede af tallet under radikalet divideret med det dobbelte af den oprindelige kvadratrod. Symbolsk kan dette repræsenteres som:
- hvis
, derefter

2. Find den afledede af tallet under radikalet. Dette er et tal eller en funktion under kvadratrodstegnet. For at bruge denne hurtige metode skal du blot finde den afledede af tallet under radikalet. Tjek følgende eksempler:
 , er rodnummeret
, er rodnummeret  . Den afledte er
. Den afledte er  .
. , er rodnummeret
, er rodnummeret  . Den afledte er
. Den afledte er  .
. , er rodnummeret
, er rodnummeret  . Den afledte er
. Den afledte er  .
.
3. Skriv den afledede af rodtallet som tæller for en brøk. Den afledte af en kvadratrodsfunktion vil indeholde en brøk. Tælleren for denne brøk er den afledede af rodtallet. Så i eksempelfunktionerne ovenfor vil den første del af den afledede se sådan ud:
 , derefter
, derefter 
 , derefter
, derefter 
 , derefter
, derefter 

4. Skriv nævneren som dobbelt den oprindelige kvadratrod. Med denne hurtige metode er nævneren det dobbelte af den oprindelige kvadratrodsfunktion. Så i de tre eksempelfunktioner ovenfor er nævnerne for de afledte:
 , derefter
, derefter 
 , derefter
, derefter 
 , derefter
, derefter 

5. Kombiner tæller og nævner for at finde den afledede. Sæt de to halvdele af brøken sammen, og resultatet bliver den afledede af den oprindelige funktion.
 , derefter
, derefter 
 , derefter
, derefter 
 , derefter
, derefter 
Artikler om emnet "Find den afledede af kvadratroden af x"
Оцените, пожалуйста статью
Populær