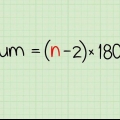Hvis du f.eks. vil beregne summen af serierne 10, 15, 20, 25, 30, så  , fordi der er fem tal i rækkefølgen.
, fordi der er fem tal i rækkefølgen. 
For eksempel i rækkefølgen 10, 15, 20, 25, 30  , og
, og  .
. 

For eksempel, hvis der er fem tal i din rækkefølge, hvor 10 er det første tal og 30 er det sidste tal, vil din formel se sådan ud:  .
. 
For eksempel:



For eksempel:


Så summen af serien (10, 15, 20, 25, 30) er lig med 100. 

Bestem antallet af tal ( ) i serien. Da du starter med tre, slutter med 24 og tilføjer syv hver gang, er talrækken 3, 10, 17, 24. (Differencefaktoren er forskellen mellem hvert tal i serien.) Det betyder at
) i serien. Da du starter med tre, slutter med 24 og tilføjer syv hver gang, er talrækken 3, 10, 17, 24. (Differencefaktoren er forskellen mellem hvert tal i serien.) Det betyder at 
Bestem den første ( ) og sidste (
) og sidste ( ) nummer i rækkefølgen. Da rækkefølgen er 3 til 24,
) nummer i rækkefølgen. Da rækkefølgen er 3 til 24,  og
og  .
. Find middelværdien af  og
og  :
:  .
. Gang middelværdien med  :
:  .
. 
Bestem antallet af led ( ) i serien. Fordi Mara sparer i 52 uger, (1 år),
) i serien. Fordi Mara sparer i 52 uger, (1 år),  .
. Bestem den første ( ) og sidste (
) og sidste ( ) nummer i rækkefølgen. Det første beløb, hun sparer, er fem euro, så
) nummer i rækkefølgen. Det første beløb, hun sparer, er fem euro, så  . For at beregne det samlede beløb, der er sparet i årets sidste uge, beregner vi
. For at beregne det samlede beløb, der er sparet i årets sidste uge, beregner vi  . så
. så  .
. Bestemmer middelværdien af  og
og  :
:  .
. Gang middelværdien med  :
:  . Så hun sparede €6890 i slutningen af året.
. Så hun sparede €6890 i slutningen af året.
Find summen af en aritmetisk rækkefølge
Indhold
En aritmetisk rækkefølge er en række tal, hvor hvert tal stiger med en konstant værdi. For summen af en aritmetisk rækkefølge kan du lægge alle tallene sammen. Dette er dog ikke rigtig praktisk, når sekvensen indeholder et stort antal led. I stedet kan du hurtigt finde summen af hver aritmetisk rækkefølge ved at gange gennemsnittet af det første og sidste tal med antallet af led i rækkefølgen.
Trin
Del 1 af 3: Analyse af din sekvens

1. Sørg for at have en aritmetisk rækkefølge. En aritmetisk rækkefølge er en ordnet liste af tal, hvor ændringen af tallene er konstant. Denne metode virker kun, hvis dit sæt tal er en aritmetisk rækkefølge.
- For at afgøre, om du har at gøre med en aritmetisk rækkefølge, skal du finde forskellen mellem det første eller sidste talpar. Sørg for, at forskellen altid er den samme.
- For eksempel er rækkefølgen af tallene 10, 15, 20, 25, 30 en aritmetisk rækkefølge, fordi forskellen mellem hvert tal konstant er fem.

2. Bestem antallet af led i din rækkefølge. Hvert tal er et led. Hvis kun ét tal er nævnt, kan du tælle dem. Hvis du kender det første tal, det sidste tal og differensfaktoren (forskellen mellem hvert tal), kan du bruge en formel til at bestemme antallet af tal. Dette tal præsenteres af variablen  .
.
 .
. , fordi der er fem tal i rækkefølgen.
, fordi der er fem tal i rækkefølgen.
3. Find det første og sidste tal i rækkefølgen. Du skal kende begge tal for at beregne summen af den aritmetiske rækkefølge. Ofte vil det første tal være et, men ikke altid. Indstil variablen  lig med det første tal i rækkefølgen, og
lig med det første tal i rækkefølgen, og  lig med det sidste tal i rækken.
lig med det sidste tal i rækken.
 lig med det første tal i rækkefølgen, og
lig med det første tal i rækkefølgen, og  lig med det sidste tal i rækken.
lig med det sidste tal i rækken. , og
, og  .
.Del 2 af 3: Beregn summen

1. Skriv formlen for at finde summen af en aritmetisk rækkefølge. Formlen er  , hvorved
, hvorved  er lig med summen af rækken.
er lig med summen af rækken.
 , hvorved
, hvorved  er lig med summen af rækken.
er lig med summen af rækken. - Bemærk, at denne formel angiver, at summen af den aritmetiske rækkefølge er lig med gennemsnittet af det første og sidste tal ganget med antallet af tal.

2. Indtast værdierne n  ,
, -en 1  og
og -en n  i formlen i. Sørg for at erstatte korrekt.
i formlen i. Sørg for at erstatte korrekt.
 ,
,  og
og  i formlen i. Sørg for at erstatte korrekt.
i formlen i. Sørg for at erstatte korrekt. .
.
3. Beregn gennemsnittet af det første og andet tal. Det gør du ved at lægge de to tal sammen og dividere med to.



4. Gang middelværdien med antallet af tal i serien. Dette giver dig summen af den aritmetiske rækkefølge.


Så summen af serien (10, 15, 20, 25, 30) er lig med 100.
Del 3 af 3: Fuldførelse af prøveproblemerne

1. Find summen af tallene fra 1 til 500. Medtag alle på hinanden følgende heltal i beregningen.
- Bestem antallet af led (
) i serien. Da du tæller alle på hinanden følgende heltal op til og med 500,
.
- Bestem den første (
) og sidste (
) nummer i rækkefølgen. Da vi antager serien 1 til 500, holder det det
og
.
- Find middelværdien af
og
:
.
- Gang middelværdien med
:
.

2. Find summen af den angivne aritmetiske rækkefølge. Det første tal i rækkefølgen er tre. Det sidste tal i rækken er 24. Forskellen er syv.
 ) i serien. Da du starter med tre, slutter med 24 og tilføjer syv hver gang, er talrækken 3, 10, 17, 24. (Differencefaktoren er forskellen mellem hvert tal i serien.) Det betyder at
) i serien. Da du starter med tre, slutter med 24 og tilføjer syv hver gang, er talrækken 3, 10, 17, 24. (Differencefaktoren er forskellen mellem hvert tal i serien.) Det betyder at 
 ) og sidste (
) og sidste ( ) nummer i rækkefølgen. Da rækkefølgen er 3 til 24,
) nummer i rækkefølgen. Da rækkefølgen er 3 til 24,  og
og  .
. og
og  :
:  .
. :
:  .
.
3. Løs følgende problem. Mara sparer 5 euro den første uge af året. Resten af året øger hun sin opsparing med 5 euro hver uge. Hvor mange penge sparede Mara i slutningen af året?
 ) i serien. Fordi Mara sparer i 52 uger, (1 år),
) i serien. Fordi Mara sparer i 52 uger, (1 år),  .
. ) og sidste (
) og sidste ( ) nummer i rækkefølgen. Det første beløb, hun sparer, er fem euro, så
) nummer i rækkefølgen. Det første beløb, hun sparer, er fem euro, så  . For at beregne det samlede beløb, der er sparet i årets sidste uge, beregner vi
. For at beregne det samlede beløb, der er sparet i årets sidste uge, beregner vi  . så
. så  .
. og
og  :
:  .
. :
:  . Så hun sparede €6890 i slutningen af året.
. Så hun sparede €6890 i slutningen af året.Artikler om emnet "Find summen af en aritmetisk rækkefølge"
Оцените, пожалуйста статью
Populær