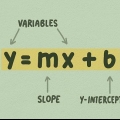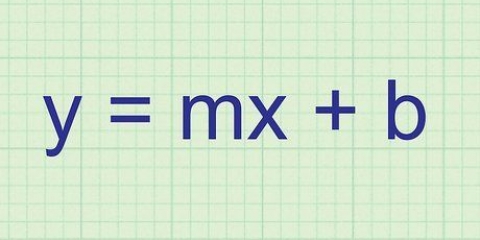Find skæringspunktet mellem en ligning og Y-aksen

Indhold

Trin
Tips

Y-skæringspunktet for en ligning er det punkt, hvor grafen for en ligning skærer y-aksen. Der er flere måder at finde dette vejkryds, afhængigt af informationen givet i begyndelsen af din kommando.

Trin

Metode 1 af 3: Find skæringspunktet med y-aksen ved hjælp af hældningen

1. Bemærk hældningen. Hældningen af `y over x` er et enkelt tal, der angiver hældningen af en linje. Denne type problemer giver dig også (x,y)-koordinat for et punkt på grafen. Hvis du ikke har begge disse detaljer, skal du fortsætte med de andre metoder nedenfor.

Eksempel 1: En lige linje med hældning 2 går igennem punktet (-3,4). Bestem skæringspunktet med denne linjes y-akse ved at bruge nedenstående trin.

Billede med titlen Find Y Intercept Trin 2

2. Lær den sædvanlige form for en lineær ligning. Enhver lige linje kan skrives som y = mx + b. Når ligningen er i denne form, er m hældningen og konstanten b skæringen med y-aksen.

Billede med titlen Find Y Intercept Trin 3

3. Erstat hældningen i denne ligning. Skriv den lineære ligning ned, men i stedet for m bruger du hældningen på din line.

Eksempel 1 (fortsat):y = mx + b
m = hældning = 2
y = 2x + b

Billede med titlen Find Y Intercept Trin 4

4. Erstat x og y med punktets koordinater. Hvis du har koordinaterne til et punkt på linjen, kan du x og y-erstatte koordinater for x og y i din lineære ligning. Gør dette for at sammenligne din opgave.

Eksempel 1 (fortsat): Punktet (3,4) er på denne linje. på dette tidspunkt, x = 3 og y = 4.
Erstat disse værdier i y = 2x +b:
4 = 2(3) + b

Billede med titlen Find Y Intercept Trin 5

5. Løs for b. Glem ikke, b er skæringspunktet med linjens y-akse. Nu b er den eneste variabel i ligningen, omarranger ligningen for at løse denne variabel og find svaret.

Eksempel 1 (fortsat):4 = 2(3) + b
4 = 6 + b
4 - 6 = b
-2 = b
Skæringspunktet mellem denne linje og y-aksen er -2.

Billede med titlen Find Y Intercept Trin 6

6. Skriv dette ned som en koordinat. Skæringspunktet med y-aksen er det punkt, hvor linjen skærer y-aksen. Da y-aksen går gennem punktet x = 0, er x-koordinaten for skæringspunktet med y-aksen altid 0.

Eksempel 1 (fortsat): Skæringspunktet med y-aksen er ved y = -2, så koordinatpunktet er (0, -2).

Metode 2 af 3: Brug af to punkter

Billede med titlen Find Y Intercept Trin 7

1. Bemærk koordinaterne for begge punkter. Denne metode behandler problemer, hvor der kun gives to punkter på en ret linje. Skriv hver koordinat på formen (x,y).

Billede med titlen Find Y Intercept Trin 8

2. Eksempel 2: En lige linje går gennem punkterne (1, 2) og (3, -4). Bestem skæringspunktet med denne linjes y-akse ved at bruge nedenstående trin.

Billede med titlen Find Y Intercept Trin 9

3. Beregn x- og y-værdierne. Hældningen eller hældningen er et mål for, hvor meget linjen bevæger sig i lodret retning for hvert trin i vandret retning. Du kender måske dette som `y over x` (

\frac{y}{x}

${frac{y}{x}}$ ). Sådan bestemmer du disse værdier ved hjælp af to punkter:

Ændringen af `y` er ændringen i lodret retning eller forskellen mellem y-værdier af de to punkter.

Ændringen af `x` er ændringen i vandret retning eller forskellen mellem x-værdier af de to punkter.

Eksempel 2 (fortsat): Y-værdierne for de to punkter er 2 og -4, så linjen stiger i lodret retning med (-4) - (2) = -6.
X-værdierne af de to punkter (i samme rækkefølge) er 1 og 3, så linjen øges vandret med 3 - 1 = 2.

Billede med titlen Find Y Intercept Trin 10

4. Divider y med x for at bestemme hældningen. Nu hvor du kender disse to værdier, kan du bruge dem i `

\frac{y}{x}

${frac{y}{x}}$ ` for at bestemme linjens hældning.

Eksempel 2 (fortsat):

s l O s e = \frac{y}{x} = - 6 2 =

$hældning={frac{y}{x}}={frac{-6}{2}}=$ -3.

Billede med titlen Find Y Intercept Trin 11

5. Tag endnu et kig på standardformen for en lineær ligning. Du kan beskrive en ret linje med formlen y = mx + b, hvorved m hældningen er og b skæringen med y-aksen. Nu hvor vi har hældningen m og et punkt (x,y), kan vi bruge denne ligning til at finde b at løse (skæringspunktet med y-aksen).

Billede med titlen Find Y Intercept Trin 12

6. Udfyld hældningen og punktet i ligningen. Tag ligningen i standardform og erstat den m ved den hældning du har beregnet. Udskift variablerne x og y ved koordinaterne for et enkelt punkt på linjen. Det er lige meget hvilket punkt du bruger.

Eksempel 2 (fortsat): y = mx + b
Hældning = m = -3, altså y = -3x + b
Linjen går gennem et punkt med (x,y)-koordinater (1,2), så 2 = -3(1) + b.

Billede med titlen Find Y Intercept Trin 13

7. Løs for b. Nu er den eneste variabel tilbage i ligningen b, skæringen med y-aksen. Omarranger ligningen så b på den ene side af ligningen, og du har dit svar. Husk at skæringspunktet med y-aksen altid har en x-koordinat på 0.

Eksempel 2 (fortsat): 2 = -3(1) + b
2 = -3 + b
5 = b
Skæringspunktet med y-aksen er (0,5).

Metode 3 af 3: Brug af en ligning

Billede med titlen Find Y Intercept Trin 14

1. Skriv linjens ligning ned. Hvis du har linjens ligning, kan du bestemme skæringspunktet med y-aksen med en lille algebra.

Eksempel 3: Hvad er skæringspunktet med linjens y-akse x + 4y = 16?
Bemærk: Eksempel 3 er en ret linje. Se slutningen af dette afsnit for et eksempel på en andengradsligning (ved brug af en variabel hævet til 2 potens).

Billede med titlen Find Y Intercept Trin 15

2. Erstat x med 0. Y-aksen er en lodret linje gennem x = 0. Det betyder, at ethvert punkt på y-aksen har en x-koordinat på 0, inklusive skæringspunktet mellem linjen og y-aksen. Indtast 0 for x i ligningen.

Eksempel 3 (fortsat): x + 4y = 16
x = 0
0 + 4 år = 16
4y = 16

Billede med titlen Find Y Intercept Trin 16

3. Løs for y. Svaret er skæringspunktet mellem linjen og y-aksen.

Eksempel 3 (fortsat): 4 år = 16

4 y 4 = \frac{16}{4}

${frac{4y}{4}}={frac{16}{4}}$
y = 4.
Skæringspunktet mellem linjen og y-aksen er 4.

Billede med titlen Find Y Intercept Trin 17

4. Bekræft dette ved at tegne en graf (valgfrit). Tjek dit svar ved at tegne ligningen så nøjagtigt som muligt. Det punkt, hvor linjen går gennem y-aksen, er skæringspunktet med y-aksen.

Billede med titlen Find Y Intercept Trin 18

5. Find skæringspunktet med y-aksen for en andengradsligning. En andengradsligning har en variabel (x eller y) hævet til anden potens. Ved at bruge den samme substitution kan du løse for y, men da andengradsligningen er en kurve, kan den skære y-aksen ved 0, 1 eller 2 punkter. Det betyder, at du ender med 0, 1 eller 2 svar.

Eksempel 4: For at finde skæringspunktet mellem

y 2 = x + 1

$y^{2}=x+1$ med y-aksen erstatter du x = 0 og løse andengradsligningen.
I dette tilfælde kan vi

y 2 = 0 + 1

$y^{2}=0+1$ løses ved at tage kvadratroden af begge sider. Husk, at du får to svar, når du tager kvadratrod: et negativt og et positivt svar.

\sqrt{y} 2 = \sqrt{1}

${sqrt{y^{2}}}={sqrt{1}}$
y = 1 eller y = -1. Disse er begge skæringspunkter med y-aksen af denne kurve.

Tips

Nogle lande bruger en c eller enhver anden variabel for b i ligningen y = mx + b. Dens betydning forbliver dog den samme; det er bare en anden notation.
For mere komplicerede ligninger kan du bruge begreberne med y isolere på den ene side af ligningen.
Når man beregner hældningen mellem to punkter, kan man x og y-trække koordinater fra i vilkårlig rækkefølge, så længe du sætter punktet i samme rækkefølge for både y og x. For eksempel kan hældningen mellem (1, 12) og (3, 7) beregnes på to forskellige måder:

Andet punkt – første punkt: $7 - 12 3 - 1 = - 5 2 = - 2.5$ ${frac{7-12}{3-1}}={frac{-5}{2}}=-2,5$
Første punkt – andet punkt: $12 - 7 1 - 3 = 5 - 2 = - 2.5$ ${frac{12-7}{1-3}}={frac{5}{-2}}=-2,5$