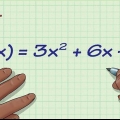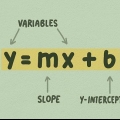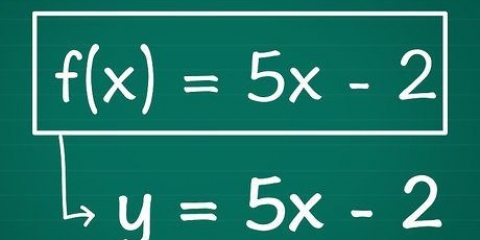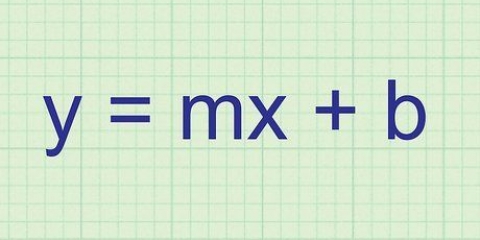Hvis hældningen er negativ, betyder det, at linjen går ned, når du går til højre. 





-1: -1 + 2 = 1 0: 0 +2 = 2 1: 1 + 2 = 3 




Gør F(x) lig med nul:
Løse:




Nogle kvadratiske funktioner, som f.eks  er aldrig negative. Så der er en asymptote ved 0.
er aldrig negative. Så der er en asymptote ved 0. Medmindre du arbejder med imaginære tal, er dette ikke muligt: 
Ligninger med komplekse eksponenter kan have mange asymptoter. 
Til sammenligningen  , kan du udfylde -1, 0, 1, -2, 2, -10 og 10. Dette giver dig et godt udvalg af tal at sammenligne.
, kan du udfylde -1, 0, 1, -2, 2, -10 og 10. Dette giver dig et godt udvalg af tal at sammenligne. Vær smart med at vælge tal. I eksemplet bemærker du hurtigt, at et negativt tegn er ligegyldigt -- for eksempel kan du stoppe med at teste -10, fordi det vil være det samme som 10. 
Antag to til fire store værdier for x, halv negativ og halv positiv, og tegn prikkerne. Hvad sker der, hvis du indsætter `uendeligt` for en variabel? Bliver funktionen uendeligt større eller mindre? Hvis graderne er ens i en brøk, som f.eks  , så dividerer du bare de to første koefficienter (
, så dividerer du bare de to første koefficienter ( for at få din endelige asymptote (-0,5).
for at få din endelige asymptote (-0,5). Hvis graderne i en brøk er forskellige, divideres ligningen i tælleren med ligningen i nævneren ved brug af polynomial lang division. 

Tegning af grafen for en funktion
Indhold
En graf for en funktion er en visuel repræsentation af en funktions opførsel på et x-y-plan. Grafer hjælper os med at forstå forskellige aspekter af funktionen, som ville være svære at forstå blot ved at se på selve funktionen. Du kan tegne tusindvis af ligninger, og der er forskellige formler for hver ligning. Der er dog altid måder at tegne en funktion på, hvis du har glemt de nøjagtige trin for den specifikke funktionstype.
Trin
Metode 1 af 3: Tegn en lineær ligning med en tangent

1. Vid at lineære funktioner er simple linjer, der er nemme at tegne, som f.eks y = 2 x + 5  . Der er én variabel og én konstant, skrevet som
. Der er én variabel og én konstant, skrevet som  i en lineær funktion, uden eksponenter, radikaler mv. Hvis du har sådan en simpel ligning, er grafen for funktionen også enkel. Andre eksempler på lineære funktioner er:
i en lineær funktion, uden eksponenter, radikaler mv. Hvis du har sådan en simpel ligning, er grafen for funktionen også enkel. Andre eksempler på lineære funktioner er:
 . Der er én variabel og én konstant, skrevet som
. Der er én variabel og én konstant, skrevet som  i en lineær funktion, uden eksponenter, radikaler mv. Hvis du har sådan en simpel ligning, er grafen for funktionen også enkel. Andre eksempler på lineære funktioner er:
i en lineær funktion, uden eksponenter, radikaler mv. Hvis du har sådan en simpel ligning, er grafen for funktionen også enkel. Andre eksempler på lineære funktioner er: 
2. Brug konstanten til at angive skæringspunktet med y-aksen. Skæringspunktet med y-aksen er det punkt, hvor funktionen krydser y-aksen på din graf. Det er med andre ord punktet hvor  . Så for at finde det skal du bare sætte x til nul og lade konstanten være i ligningen. I det foregående eksempel,
. Så for at finde det skal du bare sætte x til nul og lade konstanten være i ligningen. I det foregående eksempel,  , er skæringspunktet med y-aksen lig med y=5, dvs. punktet (0,5). Marker dette sted på dit diagram med en prik.
, er skæringspunktet med y-aksen lig med y=5, dvs. punktet (0,5). Marker dette sted på dit diagram med en prik.
 . Så for at finde det skal du bare sætte x til nul og lade konstanten være i ligningen. I det foregående eksempel,
. Så for at finde det skal du bare sætte x til nul og lade konstanten være i ligningen. I det foregående eksempel,  , er skæringspunktet med y-aksen lig med y=5, dvs. punktet (0,5). Marker dette sted på dit diagram med en prik.
, er skæringspunktet med y-aksen lig med y=5, dvs. punktet (0,5). Marker dette sted på dit diagram med en prik.
3. Find hældningen på din linje med tallet lige før variablen. I eksemplet,  , er hældningen `2`. Det er fordi 2 hører til variablen `x`. Hældningen angiver, hvor stejl en linje er, eller hvor høj linjen går, før den drejes til højre eller venstre. En større hældning betyder en stejlere linje.
, er hældningen `2`. Det er fordi 2 hører til variablen `x`. Hældningen angiver, hvor stejl en linje er, eller hvor høj linjen går, før den drejes til højre eller venstre. En større hældning betyder en stejlere linje.
 , er hældningen `2`. Det er fordi 2 hører til variablen `x`. Hældningen angiver, hvor stejl en linje er, eller hvor høj linjen går, før den drejes til højre eller venstre. En større hældning betyder en stejlere linje.
, er hældningen `2`. Det er fordi 2 hører til variablen `x`. Hældningen angiver, hvor stejl en linje er, eller hvor høj linjen går, før den drejes til højre eller venstre. En større hældning betyder en stejlere linje.
4. Lav en brøkdel af hældningen. Hældningen har at gøre med stejlheden, og stejlheden er simpelthen forskellen mellem bevægelsen op og ned, og venstre og højre. Hældningen er en brøkdel af ændringen af y sammenlignet med ændringen af x. Hvor meget skal linjen `ændre over y` før den `ændres over x`? I eksemplet kan hældningen `2` læses som  .
.
 .
.
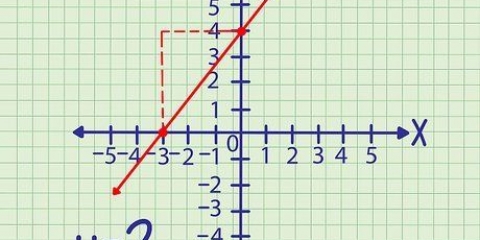
5. Start ved dit skæringspunkt med y-aksen og følg ændringerne over y og x for at tegne flere punkter. Når du kender hældningen, skal du bruge den til at tegne din lineære funktion. Start ved krydset med y-aksen, her (0,5), gå derefter 2 op og 1 til højre. Marker også dette punkt (1,7). Find yderligere 1-2 punkter for at tegne grafen.

6. Brug en lineal til at forbinde dine punkter og tegne grafen for din lineære funktion. For at undgå fejl eller grove grafer skal du finde og forbinde mindst tre separate punkter, selvom to vil være tilstrækkeligt i en nødsituation. Dette er grafen for din lineære ligning!
Metode 2 af 3: Estimering af point på en graf

1. Bestem funktionen. Tag formens funktion f(x), rigtigt y repræsenterer området, x repræsenterer domænet, og f funktionen. Som eksempel bruger vi y = x+2, hvorved f(x) = x+2.

2. Tegn to krydsede linjer på et ark papir. Den vandrette linje er dig x-aske. Den lodrette linje er dig y-aske.

3. Nummer dit diagram. Fremhæv både x-som om y-akse med tal lige langt fra hinanden. For x-akse er tallene positive til højre og negative til venstre. For y-akse er tallene positive i toppen og negative i bunden.

4. Beregn a y-værdi for 2-3 x-værdier. Overtag funktionen f(x) = x+2. Beregn nogle få værdier for y med de tilsvarende værdier for x synlig på aksen i funktionen. For mere komplicerede ligninger kan det være nødvendigt at forenkle funktionen ved først at isolere en variabel.

5. Tegn grafpunktet for hvert par. Tegn imaginære tynde lodrette linjer langs x-akse og vandret langs y-aske. Punktet, hvor disse linjer skærer hinanden, er et grafpunkt (eller brug blot millimeterpapir).

6. Fjern de imaginære linjer. Når du har tegnet alle grafpunkterne, kan du slette de imaginære linjer. Bemærk: grafen for f(x) = x ville være en linje parallel med den gennem origo (0,0), men f(x) = x+2 er forskudt to enheder (langs y-aksen) på gitteret på grund af +2 i ligningen.
Metode 3 af 3: Tegning af en kompleks funktion

1. Forstå, hvordan man grafisk repræsenterer almindelige ligningstyper. Der er lige så mange forskellige kortlægningsstrategier, som der er typer funktioner, alt for mange til at dække fuldt ud her. Hvis du synes, det er svært, og et skøn ikke virker, så tjek artikler om:
- Kvadratiske funktioner
- Rationelle funktioner
- Logaritmiske funktioner
- Uligheder (ingen funktioner, men nyttig information ikke desto mindre).

2.Bestem først nullerne. Nuller er de punkter, hvor grafen skærer den vandrette linje på grafen. Selvom ikke alle grafer har nuller, har de fleste det, og det er det første skridt, du skal tage for at få alt rigtigt. For at finde nuller skal du først sætte hele funktionen til nul og derefter løse den. For eksempel:







3. Find og marker eventuelle vandrette asymptoter (steder, hvor funktionen er umulig at nå) med en stiplet linje. Det er normalt punkter, hvor grafen ikke eksisterer, såsom hvor du dividerer med nul. Hvis din ligning har en variabel i en brøk, som f.eks  , start derefter med at nulstille bunden af brøken. Du kan kortlægge alle steder, hvor det er lig nul (i dette eksempel en stiplet linje ved x=2 og x=-2), fordi du aldrig kan dividere med nul. Brøker er dog ikke de eneste steder at finde asymptoter. Normalt er alt hvad du behøver, noget sund fornuft:
, start derefter med at nulstille bunden af brøken. Du kan kortlægge alle steder, hvor det er lig nul (i dette eksempel en stiplet linje ved x=2 og x=-2), fordi du aldrig kan dividere med nul. Brøker er dog ikke de eneste steder at finde asymptoter. Normalt er alt hvad du behøver, noget sund fornuft:
 , start derefter med at nulstille bunden af brøken. Du kan kortlægge alle steder, hvor det er lig nul (i dette eksempel en stiplet linje ved x=2 og x=-2), fordi du aldrig kan dividere med nul. Brøker er dog ikke de eneste steder at finde asymptoter. Normalt er alt hvad du behøver, noget sund fornuft:
, start derefter med at nulstille bunden af brøken. Du kan kortlægge alle steder, hvor det er lig nul (i dette eksempel en stiplet linje ved x=2 og x=-2), fordi du aldrig kan dividere med nul. Brøker er dog ikke de eneste steder at finde asymptoter. Normalt er alt hvad du behøver, noget sund fornuft: er aldrig negative. Så der er en asymptote ved 0.
er aldrig negative. Så der er en asymptote ved 0.

4. Anvend værdierne og tegn forskellige punkter. Vælg blot et par værdier for x og løs for funktionen. Lav derefter en graf over punkterne på din graf. Jo mere kompliceret grafen er, jo flere point har du brug for. Generelt er -1, 0 og 1 de nemmeste punkter at få, selvom du gerne vil have to eller tre mere på hver side af nullet for at få en god graf.
 , kan du udfylde -1, 0, 1, -2, 2, -10 og 10. Dette giver dig et godt udvalg af tal at sammenligne.
, kan du udfylde -1, 0, 1, -2, 2, -10 og 10. Dette giver dig et godt udvalg af tal at sammenligne.
5. Kortlæg funktionens slutadfærd for at se, hvad der sker, når den bliver rigtig stor. Dette giver dig en idé om den generelle retning af en funktion, normalt som en lodret asymptote. For eksempel: det ved du  til sidst bliver meget, meget stor. Bare et ekstra `x` (en million mod en million og en) gør y meget større. Der er et par måder at teste slutadfærden på, herunder:
til sidst bliver meget, meget stor. Bare et ekstra `x` (en million mod en million og en) gør y meget større. Der er et par måder at teste slutadfærden på, herunder:
 til sidst bliver meget, meget stor. Bare et ekstra `x` (en million mod en million og en) gør y meget større. Der er et par måder at teste slutadfærden på, herunder:
til sidst bliver meget, meget stor. Bare et ekstra `x` (en million mod en million og en) gør y meget større. Der er et par måder at teste slutadfærden på, herunder: , så dividerer du bare de to første koefficienter (
, så dividerer du bare de to første koefficienter ( for at få din endelige asymptote (-0,5).
for at få din endelige asymptote (-0,5).
6. Forbind prikkerne, undgå asymptotisk adfærd og slutadfærd for at estimere grafen. Når du har fem eller seks punkter, asymptoterne og en generel idé om slutadfærden, skal du bruge alle disse til at konstruere en omtrentlig version af grafen.

7. Giv perfekte grafer ved hjælp af en grafregner. Grafregnere er kraftfulde håndholdte computere, der kan levere nøjagtige grafer for enhver ligning. De giver dig mulighed for at lokalisere nøjagtige punkter, finde hældningslinjer og visualisere vanskelige ligninger med lethed. Indtast blot den nøjagtige ligning i grafafsnittet (normalt en knap mærket `F(x) = `) og tryk på grafknappen for at få en idé om funktionen.
Tips
- Grafregnere er en fantastisk måde at øve sig på. Prøv at lave en graf i hånden og brug derefter lommeregneren til at få et perfekt billede af grafen, og sammenlign derefter begge grafer.
- Hvis du virkelig ikke ved, hvad du skal gøre længere, skal du blot indtaste nogle punkter. Grundlæggende kunne du tegne hele funktionen sådan her, hvis du prøvede et uendeligt antal kombinationer af tal.
Artikler om emnet "Tegning af grafen for en funktion"
Оцените, пожалуйста статью
Lignende
Populær