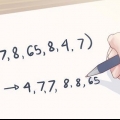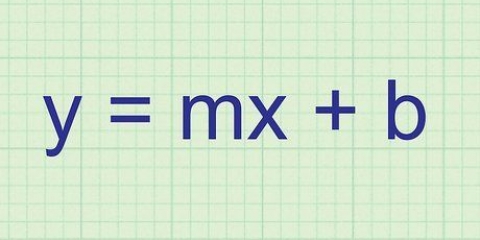Bestemmelse af omfanget af en funktion

Indhold

Trin
Tips

En funktions rækkevidde er det sæt af tal, som funktionen kan producere. Det er med andre ord det sæt af y-værdier, du får, når du indregner alle mulige x-værdier i funktionen. Dette sæt af x-værdier kaldes domænet. Hvis du vil vide, hvordan man beregner rækkevidden af en funktion, skal du følge nedenstående trin.

Trin

Metode 1 af 4: Bestemmelse af rækkevidden af en funktion med en given ligning

1. Skriv ligningen ned. Antag at du har følgende ligning: f(x) = 3x + 6x -2. Det betyder, at når du indtaster en værdi for x af ligningen, at du så har en y-får værdi. Dette er funktionen af en parabel.

Billede med titlen Find rækkevidden af en funktion i matematik trin 2

2. Find toppunktet for funktionen, hvis det er en andengradsligning. Hvis du har en ret linje eller en funktion med et polynomium eller et ulige tal, såsom f(x) = 6x+2x + 7, kan du springe dette trin over. Men hvis du har at gøre med en parabel eller en ligning, hvor x-koordinaten er i anden eller forøget med en lige potens, bliver du nødt til at tegne parablens toppunkt. For at gøre dette skal du bruge ligningen -b/2a for x-koordinaten for funktionen 3x + 6x -2, hvor 3 = a, 6 = b og -2 = c. I dette tilfælde, -b er -6 og 2a er 6, så x-koordinaten er -6/6 eller -1.

Bearbejd derefter -1 i funktionen for at få y-koordinaten. f(-1) = 3(-1) + 6(-1) -2 = 3 - 6 -2 = -5.

Parablens toppunkt er (-1,-5). Bearbejd dette i grafen ved at tegne et punkt ved x-koordinat -1 og y-koordinat -5. Dette bør være i den tredje kvadrant af grafen.

Billede med titlen Find rækkevidden af en funktion i matematik trin 3

3. Find nogle andre punkter i funktionen. For at få en fornemmelse af funktionen, bør du udfylde nogle andre værdier for x, så du kan få en idé om, hvordan funktionen ser ud, før du begynder at lede efter rækkevidden. Da det er en parabel og x er positivt, vil parablen pege opad (dalparablen). Men for at være sikker, indtaster vi et par flere værdier for x for at se, hvilke y-koordinater de giver:

f(-2) = 3(-2) + 6(-2) -2 = -2. Et punkt på grafen er (-2, -2)

f(0) = 3(0) + 6(0) -2 = -2. Et andet punkt på grafen er (0,-2)

f(1) = 3(1) + 6(1) -2 = 7. Et tredje punkt på grafen er (1, 7).

Billede med titlen Find rækkevidden af en funktion i matematik trin 4

4. Find diagrammets rækkevidde. Se nu på y-koordinaterne på grafen og find det laveste punkt, hvor grafen rører y-koordinaten. I dette tilfælde er den laveste y-koordinat i toppen af parablen, -5 og grafen strækker sig uendeligt ud over dette punkt. Det betyder, at rækkevidden af funktionen y = alle reelle tal ≥ -5.

Metode 2 af 4: Bestemmelse af rækkevidden af en funktion ved hjælp af en graf

Billede med titlen Find rækkevidden af en funktion i matematik trin 5

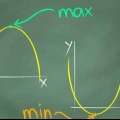
1. Find minimum af funktionen. Find den laveste y-koordinat for funktionen. Antag, at funktionen når sit laveste punkt ved -3. Denne funktion kan blive mindre og mindre, til det uendelige, så den har ikke noget fast laveste punkt - kun uendeligt.

Billede med titlen Find rækkevidden af en funktion i matematik trin 6

2. Find maksimum af funktionen. Antag at den højeste y-koordinat for funktionen er 10. Denne funktion kan også blive uendeligt meget større, så den har ikke noget fast højeste punkt – bare uendeligt.

Billede med titlen Find rækkevidden af en funktion i matematik trin 7

3. Angiv hvad rækkevidden er. Det betyder, at rækkevidden af funktionen eller området for y-koordinaterne er fra -3 til 10. Altså -3 ≤ f(x) ≤ 10. Det er funktionens omfang.

Men antag, at y = -3 er det laveste punkt på grafen, men stiger for evigt. Så er området f(x) ≥ -3, og ikke mere end det.

Antag, at grafen når sit højeste punkt ved y=10, men fortsætter derefter med at falde for evigt. Så er området f(x) ≤ 10.

Metode 3 af 4: Bestemmelse af omfanget af en relations funktion

Billede med titlen Find rækkevidden af en funktion i matematik trin 8

1. Skriv forholdet ned. En relation er et sæt ordnede par af x- og y-koordinater. Du kan se på et forhold og bestemme dets domæne og omfang. Antag, at du har at gøre med følgende relation: {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)}.

Billede med titlen Find rækkevidden af en funktion i matematik trin 9

2. Angiv y-koordinaterne for forholdet. For at bestemme forholdets rækkevidde nedskriver vi alle y-koordinater for hvert ordnet par: {-3, 6, -1, 6, 3}.

Billede med titlen Find rækkevidden af en funktion i matematik trin 10

3. Fjern alle duplikerede koordinater, så du kun har én af hver y-koordinat. Du har måske bemærket, at du har "6" to gange på listen. Fjern det, så du står tilbage med {-3, -1, 6, 3}.

Billede med titlen Find rækkevidden af en funktion i matematik trin 11

4. Skriv forholdets rækkevidde i stigende rækkefølge. Arranger derefter tallene i sættet fra mindste til største, og du har fundet rækkevidden. Området for relationen {(2, –3), (4, 6), (3, –1), (6, 6), (2, 3)} er {-3,-1, 3, 6}. Du er klar.

Billede med titlen Find rækkevidden af en funktion i matematik trin 12

5. Gør forholdet til en funktion er. For at en relation skal være en funktion, skal y-koordinaten være den samme, hver gang du indtaster et tal fra en x-koordinat. For eksempel er relationen {(2, 3) (2, 4) (6, 9)} ingen funktion, for hvis du udfylder 2`eren som x første gang, får du en 3`er som værdi, men anden gang du udfylder en 2`er, får du fire. En relation er kun en funktion, hvis du altid får det samme output for et bestemt input. Hvis du indtaster -7, bør du altid få den samme y-koordinat (hvad det end måtte være), hver gang.

Metode 4 af 4: Bestem omfanget af en funktion i en opgave

Billede med titlen Find rækkevidden af en funktion i matematik trin 13

1. Læs spørgsmålet. Antag, at du arbejder på følgende problem: "Becky sælger billetter til sin skoles talentshow for $5 hver. Det samlede beløb, hun rejser, er en funktion af antallet af billetter, hun sælger. Hvad er rækkevidden af funktionen?"

Billede med titlen Find rækkevidden af en funktion i matematik trin 14

2. Skriv opgaven som en funktion. I dette tilfælde m det beløb, der er indsamlet og t antallet af solgte billetter. Da hver billet koster 5 euro, skal du gange antallet af solgte billetter med 5 for at få det samlede beløb. Derfor kan funktionen skrives som M(t) = 5t.

For eksempel: Hvis hun sælger 2 billetter, skal du gange 2 med 5, med 10 som svaret, og dermed det samlede beløb.

Billede med titlen Find rækkevidden af en funktion i matematik trin 15

3. Bestem, hvad domænet er. For at finde rækkevidden skal du først have domænet. Domænet består af alle mulige værdier af t, der deltager i ligningen. I dette tilfælde kan Becky sælge 0 eller flere billetter – hun kan ikke sælge et negativt antal billetter. Da vi ikke kender antallet af pladser i skolens auditorium, kan vi antage, at hun i teorien kan sælge uendeligt mange billetter. Og hun kan kun sælge hele billetter, ikke en del af dem. Derfor er funktionens domæne t = ethvert positivt heltal.

Billede med titlen Find rækkevidden af en funktion i matematik trin 16

4. Bestem, hvad rækkevidden er. Intervallet er det mulige beløb, Becky kan rejse med salget. Du bliver nødt til at arbejde med domænet for at finde rækkevidden. Hvis du ved, at domænet består af et positivt heltal, og at ligningen M(t) = 5t så ved du også, at du kan indtaste et hvilket som helst positivt heltal i denne funktion for svaret eller området. For eksempel: Hvis hun sælger 5 billetter, så er M(5) = 5 x 5 eller 25 euro. Hvis hun sælger 100, så er M(100) = 5 x 100 eller 500 euro. Derfor rækkevidden af funktionen ethvert positivt heltal, der er et multiplum af fem.

Det vil sige, at ethvert positivt heltal, der er et multiplum af fem, er et muligt resultat af funktionen.

Tips

Se om du kan finde det omvendte af funktionen. Domænet for det omvendte af en funktion er lig med området for denne funktion.
I de mere vanskelige tilfælde kan det være lettere først at plotte grafen ved hjælp af domænet (hvis nødvendigt) og derefter aflæse området fra grafen.
Tjek om funktionen gentager sig. Enhver funktion, der gentager sig langs x-aksen, vil have det samme område for hele funktionen. For eksempel: f(x) = sin(x) har et interval mellem -1 og 1.