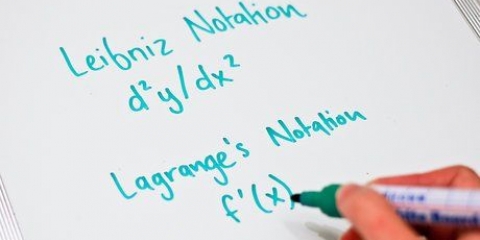Bestemmelse af maksimum- og minimumværdier for en kvadratfunktion

Indhold

Trin
Tips

Y-koordinaten for toppen eller dalen af en parabel (normalt repræsenteret ved k) er også maksimum- eller minimumværdien af andengradsligningen som repræsenteret af parablen. Lad os se, hvordan man bestemmer det!

Trin

Metode 1 af 4: For en andengradsligning på formen y = ax + bx + c

1. Beslut om du vil bestemme maksimumværdien eller minimumsværdien. Det er det ene eller det andet, du kan ikke gøre begge dele.

Den maksimale eller minimale værdi af en andengradsligning er den samme som toppen eller dalen for den funktion.
Funktionen y = ax + bx + c,
(c - b/4a) returnerer y-værdien (værdien af funktionen) som toppunktet.

Billede med titlen Find den maksimale eller minimale værdi af en kvadratisk funktion nemt Trin 1Bullet1

Hvis værdien af -en er positiv, så får du minimumsværdien, fordi parablen øverst er åben (toppunktet er det laveste punkt på grafen).

Billede med titlen Find den maksimale eller minimale værdi af en kvadratisk funktion nemt Trin 1Bullet2

Hvis værdien af -en er negativ, vil du finde den maksimale værdi, fordi parablen i bunden er åben (toppunktet er det højeste punkt på grafen).

Billede med titlen Find den maksimale eller minimale værdi af en kvadratisk funktion nemt Trin 1Bullet3

Værdien af -en kan ikke være nul, ellers har vi ikke at gøre med en andengradsligning, vel?

Billede med titlen Find den maksimale eller minimale værdi af en kvadratisk funktion nemt Trin 1Bullet4

Metode 2 af 4: For en andengradsligning på formen y = a(x-h) + k

Billede med titlen Find nemt den maksimale eller minimale værdi af en kvadratisk funktion Trin 2

1. For y = a(x-h) + k, k er værdien af funktionen i toppunktet.

k giver os maksimum- eller minimumværdien af andengradsligningen når -en er henholdsvis negativ eller positiv.

Billede med titlen Find den maksimale eller minimale værdi af en kvadratisk funktion nemt Trin 2Bullet1

Metode 3 af 4: Differentier på en andengradsligning på formen y = ax^2 + bx + c

Billede med titlen Find nemt den maksimale eller minimale værdi af en kvadratisk funktion Trin 3

1. Differentier y for x. dy/dx = 2ax + b

Billede med titlen Find nemt den maksimale eller minimale værdi af en kvadratisk funktion Trin 4

2. Bestem, hvad de afledte værdier er i form af dy/dx. Da dy/dx er den afledte funktion af en kurve, kan den afledede af en kurve bestemmes på ethvert givet tidspunkt. Den maksimale/minimum værdi kan derfor bestemmes ved at sætte disse værdier lig med 0, og derefter bestemme de tilsvarende værdier. dy/dx = 0, 2ax+b = 0, x = -b/2a