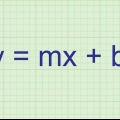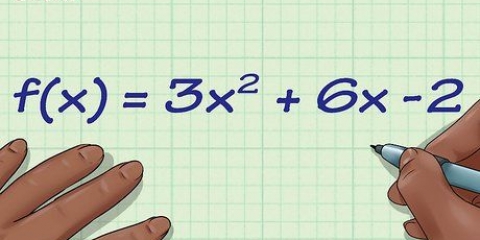At finde en derivat

Indhold

Trin
Tips
Advarsler

Derivater kan bruges til at bestemme nyttige karakteristika for en graf, såsom maksima, minima, toppe og dale og skråninger. Du kan endda bruge dem til at tegne komplekse ligninger uden en grafregner! Desværre er det ofte en vanskelig opgave at bestemme den afledede af en ligning, men denne artikel vil hjælpe dig med en række tips og tricks.

Trin

Billede med titlen Take derivatives in Calculus Step 1

1. Forstå notationen af en afledt. De følgende to måder at notere på er de mest almindelige, men der kan findes adskillige andre måder på Wikipedia.

Leibniz Notation Denne notation bruges mest, når ligningen indeholder ay og x. Dy/dx betyder bogstaveligt "den afledte af y med hensyn til x". Prøv at tænke på det som Δy/Δx for værdierne af x og y, hvor forskellen er uendelig. Denne forklaring giver naturligvis definitionen af en grænse med hensyn til den afledte: lim_h->0 (f(x+h)-f(x))/h. Anvend denne notation til den anden afledede, skriv: dy/dx.
Lagranges notation Den afledede af en funktion f skrives også som f`(x). Denne notation udtales som "funktionen f af x". Denne notation er kortere end Leibniz og bruges, når man betragter en afledt som en funktion. For højere derivater skal du blot tilføje en anden " ` " klar til "f", får den anden afledede til at ligne f``(x).

Billede med titlen Take derivatives in Calculus Step 2

2. Forstå, hvad et derivat er, og hvad det bruges til. Først, for at finde hældningen af en lineær graf, tages to punkter på linjen, og disse koordinater indsættes i ligningen (y₂ - y₁)/(X₂ - x₁). Men dette er kun muligt med lineære grafer. For andengradsligninger og derover er grafen en kurve, så forskellen mellem to punkter er ikke nøjagtig nok. For at finde hældningen af en tangent til en parabel, tages to punkter og udfyldes i ligningen for at bestemme hældningen af en buet linje: [f(x + dx) - f(x)]/dx. Dx betyder"delta x," hvad er forskellen mellem de to x-koordinater til grafens to punkter. Bemærk, at denne ligning er den samme som (y₂ - y₁)/(X₂ - x₁), men i en anden form. Da det allerede er kendt, at resultatet ikke vil være nøjagtigt, vælges en indirekte tilnærmelse. For at finde hældningen af tangenten i punktet (x, f(x)), skal dx nærme sig 0, så de to valgte punkter er næsten ens.Men du kan ikke dividere med 0, så efter at have udfyldt værdierne af de to punkter skal du eliminere dedx i nævneren. Hvis dette lykkes, gør dx lig med 0 og løs. Dette er hældningen af tangenten ved (x, f(x)). Den afledede af en ligning er den generelle ligning til at finde hældningen af enhver tangent på en graf. Dette kan virke meget svært, men eksemplerne nedenfor viser dig, hvordan du bestemmer den afledte.

Metode 1 af 4: Eksplicit differentiering

Billede med titlen Take derivatives in Calculus Trin 3

1. Brug eksplicit differentiering, hvis y allerede er på den ene side af ligningen.

Billede med titlen Take derivatives in Calculus Step 4

2. Erstat en ligning med en anden ligning [f(x + dx) - f(x)]/dx. For eksempel ligningen y = x, hvis afledede er [(x + dx) - x]/dx.

Billede med titlen Take derivatives in Calculus Step 5

3. Udvid dx yderligere for at få ligningen [dx(2x + dx)]/dx. Nu er det muligt at eliminere dx i tæller og nævner. Resultatet er 2x + dx, og når dx nærmer sig 0, bliver den afledte 2x. Dette er hældningen af enhver tangent til grafen y = x er 2x. Indtast blot værdien af et givet punkt x, som du vil finde tangenten af i ligningen.

Billede med titlen Take derivatives in Calculus Step 6

4. Lær at genkende mønstrene i den samme slags ligninger. Nedenfor finder du nogle.

Den afledte af en eksponent er eksponenten gange -1 potensen af et tal. Så den afledede af x er 5x, og den afledede af x er 3.5x. Hvis der allerede er et tal foran x, ganges det med eksponenten. For eksempel: den afledte af 3x er 12x.

Den afledte af enhver konstant er nul. Så den afledede af 8 er 0.

Den afledte sum er summen af hver enkelt afledt. For eksempel: den afledte af x + 3x er 3x + 6x.

Den afledte af et produkt er den første faktor gange den afledte af den anden faktor plus den anden faktor gange den afledte af den første. For eksempel er den afledte af x(2x + 1) x(2) + (2x + 1)3x, hvilket er lig med 8x + 3x.

Afledt af en kvotient (f.eks. f/g) er [g(afledt af f) - f(afledt af g)]/g. For eksempel: den afledte af (x + 2x - 21)/(x - 3) er (x - 6x + 15)/(x - 3).

Metode 2 af 4: Implicit differentiering

Billede med titlen Take derivatives in Calculus Step 7

1. Brug implicit differentiering, når din ligning ikke bare kan skrives med y på den ene side af lighedstegnet. Selvom du skriver det med y på den ene side, ville det stadig være en opgave at beregne dy/dx. Nedenfor er et eksempel på, hvordan man løser denne form for ligning.

Billede med titlen Take derivatives in Calculus Step 8

2. I dette eksempel, xy + 2y = 3x + 2y, erstatter du jey med f(x), så det er tydeligt, at dette faktisk er en funktion. Ligningen bliver så xf(x) + 2[f(x)] = 3x + 2f(x).

Billede med titlen Take derivatives in Calculus Step 9

3. For at finde den afledede af denne ligning skal du differentiere (et imponerende ord for at finde den afledede) dine begge sider af ligningen med hensyn til x. Ligningen bliver så xf`(x) + 2xf(x) + 6[f(x)]f`(x) = 3 + 2f`(x).

Billede med titlen Take derivatives in Calculus Step 10

4. Erstat f(x) igen med y. Pas på ikke at gøre dette med f`(x), da dette er meget forskelligt fra f(x).

Billede med titlen Take derivatives in Calculus Step 11

5. Løs for f`(x). Svaret i dette eksempel er (3 - 2xy)/(x + 6y - 2).

Metode 3 af 4: Højere derivater

Billede med titlen Take derivatives in Calculus Step 12

1. At tage den højere afledede af en funktion betyder blot at tage den afledede af den afledte. For eksempel, hvis den tredje afledte bliver spurgt, tager du den afledte af den afledte afledte. For nogle ligninger bliver en højere afledt lig med 0.

Metode 4 af 4: Kædereglen

Billede med titlen Take derivatives in Calculus Step 13

1. Hvis y er en differentierbar funktion af z, og z er en differentierbar funktion af x, så er y en sammensat funktion af x, og den afledede af y med hensyn til x (dy/dx) er (dy/du)*(du) /dx). Kædereglen kan også være en sammensat ligning, som denne: (2x - x). For at finde den afledte af dette; tænk bare på samme måde, som du gør med produktlinjen. Multiplicer ligningen med eksponenten og reducer eksponenten med 1. Gang derefter ligningen med den afledede, der falder ind under eksponenten (i dette tilfælde 2x^4 - x). Svaret på dette problem bliver så 3(2x - x)(8x - 1).

Tips

Når du ser et tilsyneladende uløseligt problem, skal du ikke bekymre dig. Prøv at dele problemet op i mindre dele ved at anvende produktreglerne, kvotientreglen mv. Derefter differentieres de enkelte dele.
Øv produktreglen, kvotientreglen, kædereglen og vigtigst af alt implicit differentiering, da disse kan være ret vanskelige ud fra calculus.
Kend din lommeregner; prøv de forskellige funktioner i din lommeregner for at lære, hvordan de fungerer. Det er bestemt værdifuldt at vide, hvordan man bruger tangent- og afledte funktioner, hvis din lommeregner har dem.
Lær de mest almindeligt anvendte trigonometriske derivater udenad, og hvordan man arbejder med dem.