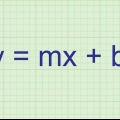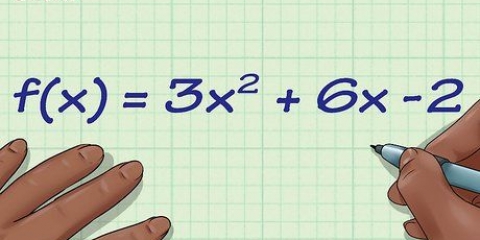(3-5)/(8-2) = -2/6 = -1/3 Linjens hældning er -1/3. For at finde denne hældning skal du forenkle 2/6 til dens mindste værdier, 1/3, da både 2 og 6 er delelige med 2. 
Den negative reciproke af -1/3 er 3, fordi 3/1 er den reciproke af 1/3 og tegnet er ændret fra negativ til positiv. 

3 --> y = mx + b = y = 3x + b 
(5, 4) --->y = 3x + b = 4 = 3(5) + b = 4 = 15 + b 
4 = 15 + b = -11 = b b = -11 
y = mx + b y = 3x - 11 Ligningen for den vinkelrette halveringslinje gennem punkterne (2, 5) og (8, 3) er y = 3 x - 11.
Bestemmelse af den vinkelrette halveringslinje af to punkter
En halveringslinje er en linje, der halverer et segment, der er forbundet med to punkter i en vinkel på 90 grader. For at finde den vinkelrette halveringslinje af to punkter, skal du blot finde deres midtpunkter og den reciproke og derefter anvende svarene på ligningen for en linje med formen y = mx + b. Hvis du vil vide, hvordan du finder den vinkelrette halveringslinje af to punkter, skal du følge trinene nedenfor.
Trin
Metode 1 af 2: Indsaml information

1. Find midten af de to punkter. Find midtpunktet af to punkter ved at anvende punkterne på midtpunktsformlen: [(X1 + x2)/2,( y1 + y2)/2]. Det betyder, at du tager et gennemsnit af x- og y-koordinaterne for de to punkter, hvilket giver dig midten af de to koordinater. Antag, at vi arbejder med koordinaterne (x1, y1) af (2, 5) og koordinaterne (x2, y2) fra (8, 3). Du bestemmer midten af de to punkter som følger:
- [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- Koordinaterne for midten af (2, 5) og (8, 3) er (5, 4).

2. Find hældningen af de to punkter. For at finde hældningen (hældningen) af de to punkter skal du anvende punkterne på hældningsformlen: (y2 - y1) / (x2 - x1). Hældningen af en linje er afstanden af en lodret ændring over afstanden af en tilsvarende vandret ændring. Du bestemmer linjens hældning gennem punkterne (2, 5) og (8, 3) som følger:

3. Find den negative reciproke af hældningen af de to punkter. For at finde den negative reciproke af en hældning, tag den reciproke af hældningen og skift tegnet. Du kan finde den reciproke af et tal ved at invertere x- og y-koordinaterne. Den negative reciproke på 1/2 er -2/1, eller kun -2; den gensidige på -4 er 1/4.
Metode 2 af 2: Beregn linjens ligning

1. Skriv ligningen for en linje på formen y = mx + b. Ligningen for en linje gennem to punkter har formen `y = mx + b ` hvor x- og y-koordinaterne på linjen er repræsenteret af `x` og `y`, `m` repræsenterer linjens hældning, og `b` repræsenterer linjens skæringspunkt med y-aksen. Når du har skrevet denne ligning, kan du begynde at finde ligningen for den vinkelrette halveringslinje af de to punkter.

2. Anvend den negative reciproke af den oprindelige hældning på ligningen. Den negative reciproke af hældningen af punkterne (2, 5) og (8, 3) var 3. `m` i ligningen repræsenterer hældningen, så indtast 3 for `m` i ligningen for en ret linje, y = mx + b.

3. Anvend midtpunktet på linjen. Du ved allerede, at midtpunkterne i punkterne (2, 5) og (8, 3) er lig med (5, 4). Da den vinkelrette halveringslinje går gennem midtpunkterne på de to linjer, kan du anvende koordinaterne for midtpunkterne på linjens ligning. Du skal blot udfylde (5, 4) i stedet for linjens x- og y-koordinater.

4. Løs for krydset. Du har fundet tre af de fire variable i linjens ligning. Nu har du nok information til at bestemme den resterende variabel `b`, skæringspunktet mellem denne linje og y-aksen. Isoler variablen `b` for at bestemme dens værdi. Træk 15 fra begge sider af ligningen.

5. Skriv ligningen for den vinkelrette halveringslinje. For at skrive ligningen for den vinkelrette halveringslinje erstatter du hældningen af linjen (3) og skæringspunktet med y-aksen (-11) i ligningen på formen y = mx + b. Indtast ikke noget for x- og y-koordinaterne, for med denne ligning kan du finde en hvilken som helst koordinat på linjen ved at udfylde en x- eller en y-koordinat.
Artikler om emnet "Bestemmelse af den vinkelrette halveringslinje af to punkter"
Оцените, пожалуйста статью
Lignende
Populær