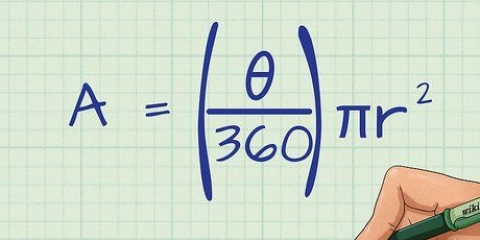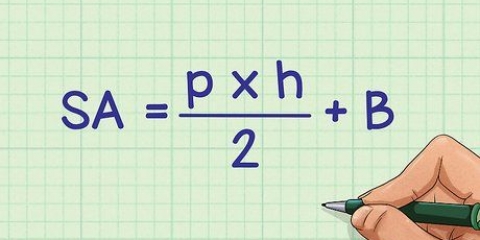Hvis du vil beregne arealet af en firkant, kan du spare tid ved at bruge en lommeregner og kvadrere en side. Så hvis den ene side er fire meter, skal du klikke på 4 og derefter på den firkantede knap på din lommeregner for at få svaret. Kvadring multiplicerer et tal med sig selv. 
Dette omtales også som cm i kvadrat eller skrevet med et lille `2` øverst til højre på enheden i stedet for ordet `firkantet`. 


























Bestemmelse af arealet af en form
Indhold
Der er mange forskellige former og lige så mange grunde til, at du gerne vil kende deres overfladeareal! Uanset om du laver dit hjemmearbejde eller prøver at finde ud af, hvor meget maling du skal bruge for at male din stue om, kan wikiHow hjælpe! Bare start med trin 1 nedenfor for at lære, hvordan man beregner arealet af en form.
Trin
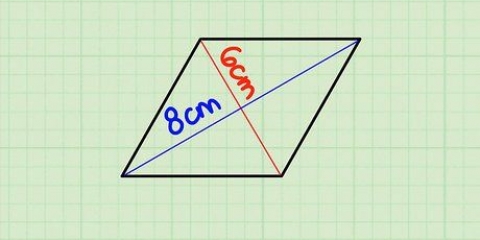
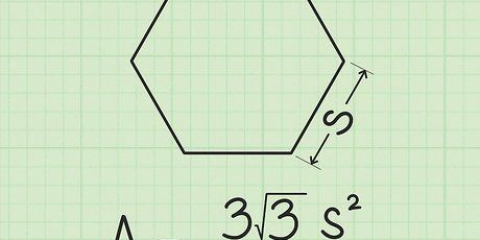
Metode 1 af 7: Firkanter, rektangler og parallellogrammer

1. Mål bredden og højden. Start med at bestemme bredden og højden af formen (med andre ord ved at bestemme længden af to tilstødende sider).
- For et parallelogram skal du bruge basen og den lodrette højde, men de er de samme som bredden og højden.
- I den virkelige verden skal du selv måle dette, men til dit hjemmearbejde vil disse mål blive givet sammen med formen.

2. Multiplicer siderne. Multiplicer siderne sammen. For eksempel, hvis du har et rektangel med en højde på 16 cm og en bredde på 42 cm, skal du gange 16 x 42.

3. Bestem resultatet. Det resulterende tal fra multiplikationen er arealet af din form, skrevet som `kvadratenheder`. Så arealet af vores rektangel er 672 kvadrat cm.
Metode 2 af 7: Trapez

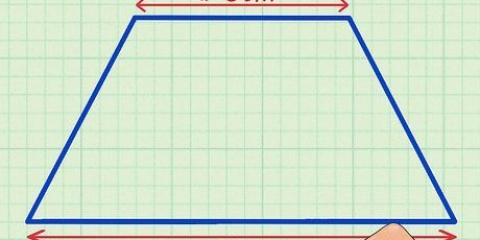
1. Tag dine mål. Du skal bruge målene fra bunden, toppen og den lodrette højde. Basen og toppen er parallelle, mens højden er målt langs en af siderne med vinklen.
- I den virkelige verden skal du selv måle dette, men til dit hjemmearbejde vil disse mål blive givet sammen med formen.

2. Læg længden af højden og basen sammen. Antag, at højden er 5 cm og bunden er 7 cm. Dette giver os en værdi på 12.

3. Gang denne værdi med 1/2. dette giver os en værdi på 6.

4. Gang denne værdi med højden. Antag, at vi har et trapez på 6 cm. Dette giver os en værdi på 36.

5. Bestem resultatet. Det resulterende tal efter multiplikation med højden er arealet af trapez. Så med en trapez på 5 x 6 x 7 er arealet 36 cm.
Metode 3 af 7: Cirkel

1. Bestem radius. For at finde arealet af en cirkel skal du kende dens radius. Dette er afstanden fra midten af cirklen til kanten. Det kan du også bestemme med diameteren, eller bredden af cirklen, hvorefter du dividerer den med to.
- I den virkelige verden skal du selv måle dette, men til dit hjemmearbejde vil disse mål blive givet sammen med formen.

2. Firkant radius. Multiplicer radius med sig selv. Antag, at vi har en radius på 8 meter, dette giver os en værdi på 64.

3. Gang med pi. Pi (π) er et tal med mange decimaler, og bruges i mange beregninger. Hvis du bruger en lommeregner, skal du bruge pi-funktionen for at få et meget præcist resultat. Hvis ikke, kan du afrunde pi (og ignorere de fleste decimaler) til 3,14159. Dette giver os et produkt efter at have ganget 201,06176.

4. Bestem resultatet. Det resulterende tal (201.06176 i dette tilfælde) er arealet af cirklen. Så vi får et resultat på 201,06176 m.
Metode 4 af 7: Segmenter

1. Bestem dimensionerne. Segmenter er dele af en cirkel, der ligner vifter. Du måler radius af den oprindelige cirkel, eller den ene side af din `fan`, samt vinklen på punktet. Antag, at du har en radius på 14 cm og en vinkel på 60.
- I den virkelige verden skal du selv måle dette, men til dit hjemmearbejde vil disse mål blive givet sammen med formen.

2. Firkant radius. Multiplicer radius med sig selv. Dette giver os en værdi på 196 (14x14).

3. Gang med pi. Pi (π) er et tal med mange decimaler, og bruges i mange beregninger. Hvis du bruger en lommeregner, skal du bruge pi-funktionen for at få et meget præcist resultat. Hvis ikke, kan du afrunde pi`en (og ignorere de fleste decimaler) og kun gange med 3,14159. Dette giver os en værdi på 615,75164.

4. Divider vinklen med 360. Så tager du vinklen på punktet og dividerer det tal med 360 (antallet af grader i en cirkel). I dette tilfælde får vi en værdi på omkring 0,166. Dette er teknisk set et gentaget tal, men vi vil runde det op for at gøre matematikken lidt nemmere.

5. Gang det resulterende tal med det tal, du beregnede tidligere. Gang det tal, du får, når du dividerer med 360 med det tal, du beregnede tidligere efter at have ganget med pi. I dette tilfælde er resultatet omkring 102.214.

6. Beregn resultatet. Det endelige tal er arealet af dit segment, hvilket giver segmenter på 102.214 cm.
Metode 5 af 7: Ellipser

1. Bestem dimensionerne. For at finde arealet af en ellipse skal du kende de to `stråler`, som du kan tænke på som bredden og højden, hver divideret med. Disse er målene fra midten til midten af den lange side, og fra midten til midten af den korteste side. Målelinjerne skærer hinanden i rette vinkler.
- I den virkelige verden skal du selv måle dette, men til dit hjemmearbejde vil disse mål blive givet sammen med formen.

2. Multiplicer de to stråler. Antag, at ellipsen er 6 cm bred og 4 cm høj. Dette giver os radier på 3 cm og 2 cm. Nu gange vi disse tal sammen, og vi får produktet 6 (3x2).

3. Gang dette tal med pi. Pi (π) er et usædvanligt langt tal og bruges i mange beregninger. Hvis du bruger en lommeregner, skal du bruge pi-funktionen for at få et meget præcist resultat. Hvis ikke, kan du afrunde pi`en (og ignorere de fleste decimaler) og kun gange med 3,14159. Dette giver os en værdi på 18,84954.

4. Bestem resultatet. Det resulterende tal er arealet af din ellipse. I dette tilfælde betyder det, at vores ellipse er 18.84954 cm.
Metode 6 af 7: Trekant

1. Bestem dine dimensioner. Du skal kende dimensionerne af trekantens base såvel som højden. Basen kan være en hvilken som helst side af trekanten, så længe du kan måle højden. Antag, at vi har en trekant med en base på 3 meter og en højde på 1 meter.
- I den virkelige verden skal du selv måle dette, men til dit hjemmearbejde vil disse mål blive givet sammen med formen.

2. Gang basen med højden. I dette tilfælde får vi en værdi på 3 (3x1).

3. Gang denne værdi med 1/2. Dette giver os en værdi på 1,5.

4. Bestem resultatet. Den resulterende værdi er arealet af trekanten. Så vi får et resultat på 1,5 m.
Metode 7 af 7: Komplekse former

1. Bryd formen op i sektioner. Du starter med at bestemme arealet for komplekse former ved at bryde formen op i geometriske figurer, som vist ovenfor. I hjemmeopgaver vil det være indlysende, hvilke former det vil være, men i den virkelige verden bliver du nødt til at dele et fly op i mange forskellige former for at få et præcist resultat.
- Et godt sted at starte er ved at lede efter rette vinkler og parallelle linjer. Disse danner grundlaget for mange former.

2. Beregn arealet af de enkelte figurer. Brug instruktionerne ovenfor til at bestemme arealet af de forskellige former.

3. Tilføj figurerne sammen. Tilføj de resulterende områder sammen for at finde det samlede areal af din form.

4. Brug alternative metoder. Der er andre tricks, du også kan prøve afhængigt af formen. Du kan også valgfrit tilføje et imaginært rum for at gøre formen til en standard geometrisk form, og derefter trække arealet af det imaginære rum efter at have bestemt resultatet.
Tips
- Brug denne lommeregner hvis du har brug for mere hjælp og vil vide, hvordan matematikken fungerer.
- Hvis du synes, det er svært, så spørg nogen om hjælp!
Advarsler
- Hold enhederne for dine aflæsninger de samme. Det er ikke meningen, at tal skal blandes sammen!
- Det er altid en god idé at dobbelttjekke dit svar!
Artikler om emnet "Bestemmelse af arealet af en form"
Оцените, пожалуйста статью
Populær