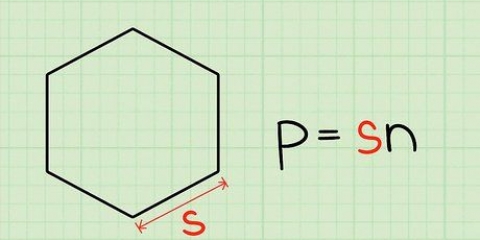
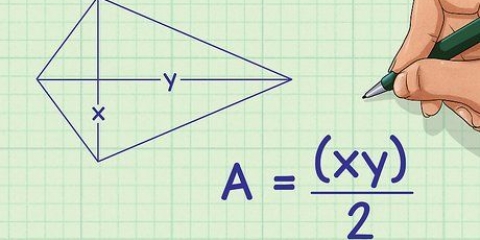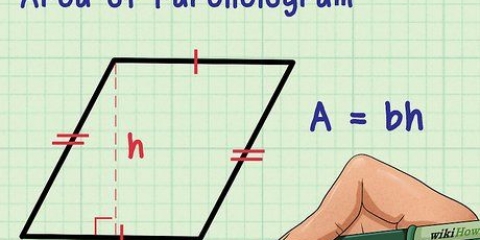Hvis du kender omkredsen, skal du dividere den med 6 for at beregne længden af en side. For eksempel: længden af omkredsen er 54 cm; divider dette med 6 og du får 9 cm som svar på længden af siden.
Hvis du kun kender apotemet, så kan du finde længden af en side ved at indtaste apotemets værdi i formlen a = x√3 og gang svaret med 2. Dette skyldes, at apotemet danner siden af en 30-60-90 trekant. For eksempel, hvis apotemet er 10√3, så er x lig med 10 og længden af en side er 10 x 2 = 20. 

(3√3 x 9)/2 = (3√3 x 81)/2 = (243√3)/2 = 420.8/2 = 210.4 cm 


Apotemet er siden x√3. Derfor kan du indtaste denne værdi i formlen a = x√3. For eksempel, hvis længden af apotemet er 5√3, så ifølge formlen: 5√3 cm = x√3 eller x = 5 cm. Ved at løse x har du fundet længden af trekantens korte side, x = 5. Da det er halvdelen af længden af den ene side af sekskanten, kan du gange dette med 2 for at få den fulde længde af siden. 5 cm x 2 = 10 cm. Nu hvor du ved, at den fulde længde af den ene side er lig med 10, skal du bare gange den med 6 for at få omkredsen af sekskanten. 10 cm x 6 = 60 cm 
Areal = 1/2 x omkreds x apotem Areal = 1/2 x 60 cm x 5√3 cm 
1/2 x 60 cm x 5√3 cm = 30 x 5√3 cm = 150√3 cm = 259. 8 cm 

4 x 7 = 28 9 x 2 = 18 11 x 2 = 22 2 x 5 = 10 1 x 7 = 7 4 x 10 = 40 28 + 18 + 22 + 10 + 7 + 40 = 125 
10 x 9 = 90 7 x 11 = 77 2 x 2 = 4 2 x 1 = 2 5 x 4 = 20 7 x 4 = 28 90 + 77 + 4 + 2 + 20 + 28 = 221 




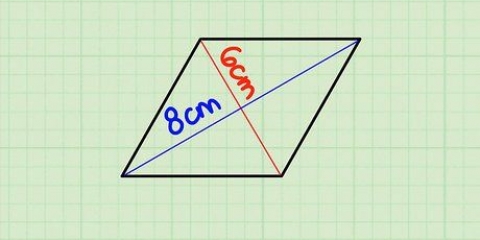
En bestemt type uregelmæssig sekskant består af to parallelogrammer. For at beregne arealer af disse skal du gange grundtallet gange højden, ligesom et rektangel, og derefter lægge deres arealer sammen.
Beregn arealet af en sekskant
Indhold
En sekskant eller sekskant er en polygon med seks sider og vinkler. En regulær sekskant har seks lige store sider og vinkler og består af seks ligesidede trekanter. Der er en række måder at beregne arealet af en uregelmæssig eller regulær sekskant. Hvis du vil vide hvordan, skal du følge disse trin.
Trin
Metode 1 af 4: Arealet af en regulær sekskant med en given side

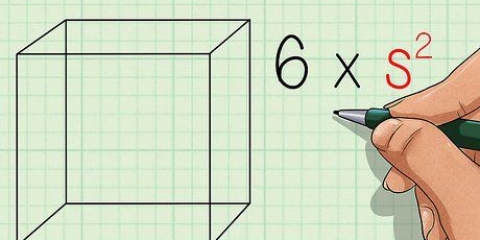
1. Skriv formlen ned for at beregne arealet af en sekskant, hvis du kender længden af en side. Da en regulær sekskant består af seks ligesidede trekanter, er formlen for at finde arealet af en sekskant afledt af formlen til beregning af arealet af en ligesidet trekant. Formlen for dette er: Areal = (3√3 s)/ 2 hvor er` er længden af den ene side af den regulære sekskant.

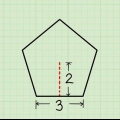
2. Bestem længden af siden. Hvis du allerede kender længden, så skriv den ned. I dette tilfælde er længden af den ene side 9 cm. Hvis du ikke kender længden, men ved hvor lang omkredsen er, eller du kender deapothema (længden af linjen fra midten af sekskanten, der er vinkelret på en side), kan du stadig få længden af siden af en beregnet sekskant. Sådan gør du det:

3. Indtast længden af siden i formlen. Da du ved, at længden af den ene side af trekanten er 9, kan du bare sætte dette ind i den originale formel. Det ser sådan ud: Areal = (3√3 x 9)/2

4. Forenkle dit svar. Find værdien af ligningen og skriv dit svar ned. Husk, da du beregner arealet, skal svaret være i kvadratmeter. Her kan du læse, hvordan du gør
Metode 2 af 4: Arealet af en regulær sekskant med et kendt apotem

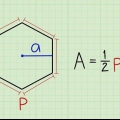
1. Skriv ned formlen for at beregne arealet af en sekskant med en given apotem. Formlen er enkel: Areal = 1/2 * omkreds* apotem.

2. Bemærk apotemet. Antag, at apotemet er 5√3 cm.

3. Brug apotemet til at finde omkredsen. Da apotemet er vinkelret på siden af sekskanten, danner det den ene side af en 30-60-90 trekant. Siderne i en 30-60-90 trekant har forholdet: xx√3-2x, hvor x er længden af den korteste side (modsat vinklen på 30 grader), x√3 er længden af den lange side (modsat vinklen på 60 grader) og 2x hypotenusen.

4. Indtast alle kendte værdier i formlen. At beregne omkredsen var den sværeste del. Nu skal du bare løse apotemet og omkredsen ved hjælp af formlen:

5. Forenkle dit svar. Forenkle udtrykket, indtil du har fjernet alle kvadratrødder fra ligningen. Sørg for, at dit endelige svar er i kvadratmeter.
Metode 3 af 4: Beregn arealet af en ujævn sekskant med givne hjørner

1. Angiv x- og y-koordinaterne for alle hjørner. Hvis du kender hjørnerne af sekskanten, er det første du gør en tabel med to kolonner og syv rækker. Hver række er opkaldt efter de seks punkter (punkt A, punkt B, punkt C osv.), og hver kolonne er opkaldt efter x- eller y-koordinaterne for disse punkter. Angiv x- og y-koordinaterne fra punkt A til punkt F. Gentag koordinaterne for punkt A i slutningen af listen. Lad os tage følgende eksempel med formatet Navn:(x,y):
- A: (4, 10)
- B: (9, 7)
- C: (11, 2)
- D: (2, 2)
- E: (1, 5)
- F: (4, 7)
- A (igen): (4, 10)

2. Multiplicer x-koordinaten for hvert punkt med y-koordinaten for det næste punkt. Placer resultaterne til højre for tabellen. Læg derefter resultaterne sammen.

3. Multiplicer y-koordinaten for hvert punkt med x-koordinaten for det næste punkt. Læg resultaterne sammen.

4. Træk den anden sum fra den første sum. Træk 221 fra 125. 125 - 221 = -96. Tag nu den absolutte værdi af dette svar: 96. Område kan kun være positivt.

5. Divider den beregnede forskel med to. At dividere 96 med 2 giver arealet af den uregelmæssige sekskant. 96/2 = 48. Husk at enheden for dit svar er kvadratmeteren. Svaret på spørgsmålet er derfor 48 m.
Metode 4 af 4: Andre metoder til beregning af arealet af en sekskant

1. At finde arealet af en sekskant, hvor et toppunkt er ukendt. Hvis du ved, du har at gøre med en regulær sekskant med manglende trekanter, er det første du gør, at beregne arealet, som om sekskanten var komplet. Beregn derefter bare arealet af trekanter dannet af hjørnerne og træk det fra det samlede areal. Dette returnerer arealet af den uregelmæssige sekskant.
- Et eksempel: Hvis du har beregnet, at arealet af den regulære sekskant er 60 cm, og du ved, at arealet af de manglende trekanter er 10 cm, så er arealet af den uregelmæssige sekskant: 60 cm - 10 cm = 50 cm.
- Hvis du ved, at sekskanten mangler præcis én trekant, er det også muligt at finde arealet af den uregelmæssige sekskant ved at gange arealet af den regulære sekskant eller det samlede areal med 5/6, fordi den uregelmæssige sekskant optager et område, der eksisterer fra 5 af de 6 trekanter i den regulære sekskant. Hvis der mangler to, ganges med 4/6, og så videre.

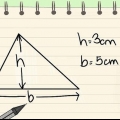
2. Bryd en uregelmæssig sekskant i andre trekanter. Det kan være, at den uregelmæssige sekskant består af fire trekanter med uens form. For at finde hele arealet af denne sekskant skal du finde arealet af hver enkelt trekant og derefter lægge dem sammen. Der er flere måder at finde arealet af en trekant på, afhængigt af hvad du ved.

3. Se efter andre former i den uregelmæssige sekskant. Hvis du ikke kan finde trekanter, så se om du kan finde andre former - måske en firkant eller et rektangel. Når du har opdaget de andre former, skal du lægge områderne sammen for at beregne det for hele sekskanten.
Artikler om emnet "Beregn arealet af en sekskant"
Оцените, пожалуйста статью
Populær