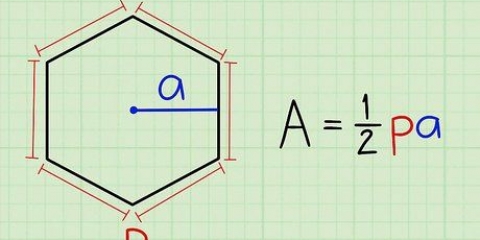
For eksempel, hvis en ligebenet trekant har sider på 5 cm, 5 cm og 6 cm, så er siden på 6 cm basis. Hvis en trekant har tre lige store sider (og derfor er ligesidet), så kan du vælge en hvilken som helst side som basis. En ligesidet trekant er en speciel slags ligebenet trekant, men du kan finde dens areal på samme måde. 
I en ligebenet trekant rører denne linje altid basen i sit nøjagtige centrum. 
En af de korte sider er lig med halvdelen af basen:  .
. Den anden korte side er højden h. Hypotenusen (hypotenusen) i den retvinklede trekant er en af de to lige store sider af den ligebenede trekant. Lad os få det her s at nævne. 
Du har sikkert lært Pythagoras sætning if  . At skrive dette som `sider` og `hypotenuse` forhindrer dig i at forveksle disse med variablerne i trekanten.
. At skrive dette som `sider` og `hypotenuse` forhindrer dig i at forveksle disse med variablerne i trekanten. 


 .
.
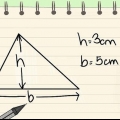
For eksempel har du en ligebenet trekant med siderne 5 cm, 5 cm og 6 cm. b = 6 og s = 5. Brug disse værdier i din formel:





 cm.
cm. 
For at fortsætte med eksemplet: 5-5-6 trekanten har en base på 6 cm og en højde på 4 cm. A = bh
A = ½ (6 cm) (4 cm)
A = 12 cm. 
Hvad er arealet af en trekant med siderne 8 cm, 8 cm og 4 cm? Den ujævne side er 4 cm, og bunden b. Højden 


Forenkle kvadratroden ved at faktorisere: 
Overflade 


Lad dette svar være som nævnt, eller brug en lommeregner til et decimalestimat (ca. 15,49 cm2). 

Denne linje deler θ perfekt i halvdelen. Hver retvinklet trekant har en vinkel på ½θ, eller i dette tilfælde (½)(120) = 60 grader. 
cos(θ/2) = h/s cos(60º) = h / 10 h = 10cos(60º) 
sin(θ/2) = x/s sin(60º) = x / 10 x = 10sin(60º) 





Ved hjælp af en lommeregner (indstillet til grader) får du cirka 43,3 cm2 som svar. Alternativt kan du bruge egenskaberne for trigonometri til at forenkle dem til A = 50sin(1200). 

s er længden af en af de to lige store sider. Θ er vinklen mellem de to lige store sider.
Beregn arealet af en ligebenet trekant
Indhold
En ligebenet trekant er en trekant med to sider af samme længde. Disse to lige store sider har altid samme vinkel til basen (den tredje side) og mødes direkte over midten af basen. Du kan selv teste dette med en lineal og to blyanter af samme længde: Hvis du forsøger at vippe trekanten i én retning, vil enderne af blyanterne ikke mødes. Med disse specielle egenskaber ved den ligebenede trekant kan arealet beregnes med blot nogle få stykker data.
Trin
Metode 1 af 2: Bestemmelse af arealet ved hjælp af længderne af hver side

1. Tag arealet af et parallelogram. Firkanter og rektangler er parallellogrammer, ligesom enhver firesidet form, hvor to par sider er parallelle med hinanden. Alle parallelogrammer har en simpel arealformel: areal er lig med base ganget med højde, eller A = bh. Hvis du placerer et imaginært parallelogram opretstående på en vandret flade, er bunden længden af den side, figuren er på. Højden er afstanden fra basen til det højeste punkt (som du ville forvente); dvs afstanden fra basen til den modsatte side. Mål altid højden i en ret vinkel (90 grader) i forhold til basen.
- For firkanter og rektangler er højden lig med længden af en lodret side, da disse sider er vinkelret på jorden.

2. Sammenlign trekanter og parallellogrammer. Der er et simpelt forhold mellem disse to former. Ved at skære et parallelogram i to langs diagonalen opdeles det i to lige store trekanter. Ligeledes kan du forbinde to identiske trekanter sammen for at danne et parallelogram. Det betyder, at arealet af en trekant kan skrives som A = bh, nøjagtig halvdelen af størrelsen af et tilsvarende parallelogram.

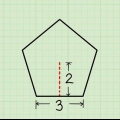
3. Find bunden af den ligebenede trekant. Nu har du formlen, men hvad er `basen` og `højden` af en ligebenet trekant præcist? Basen er den nemme del: Tag bare den tredje, ulige side af den ligebenede trekant.

4. Tegn en linje mellem basen og det modsatte toppunkt. Sørg for, at linjen rører basen i en ret vinkel. Længden af denne linje er højden af trekanten og er derfor mærket h. Når du får værdien af h beregnet, kan du bestemme arealet.

5. Se den ene halvdel af den ligebenede trekant. Bemærk, at højden deler den ligebenede trekant i to ens retvinklede trekanter. Se på en af dem og peg på de tre sider:
 .
.
6.Brug Pythagoras sætning. Hvis du kender to sider af en retvinklet trekant og vil finde den tredje, kan du bruge Pythagoras sætning: (side 1) + (side 2) = (hypotenus) Erstat de variable, vi bruger i denne opgave, og du får  .
.
 .
. . At skrive dette som `sider` og `hypotenuse` forhindrer dig i at forveksle disse med variablerne i trekanten.
. At skrive dette som `sider` og `hypotenuse` forhindrer dig i at forveksle disse med variablerne i trekanten.
7. Løs for h. Husk at du har arealformlen b og h brugt, men som du ikke kender værdien af h ved det ikke endnu. Omskriv formlen h at løse:


 .
.
8. Erstat værdierne af din trekant med h Nu hvor du kender denne formel, kan du bruge den til en ligebenet trekant, hvis sider du kender. Indtast blot længden af basen for b og længden af en af de lige sider for s, og beregn bagefter h.





 cm.
cm.
9. Brug basis- og højdeværdierne i arealformlen. Nu har du, hvad du skal bruge for at bruge formlen fra begyndelsen af dette afsnit: Areal = ½bh. Erstat værdierne for b og h i denne formel og beregn svaret. Glem ikke at skrive dit svar i kvadratiske enheder.
A = ½ (6 cm) (4 cm)
A = 12 cm.

10. Prøv et sværere eksempel. De fleste ligebenede trekanter er sværere at arbejde med end i det foregående eksempel. Højde indeholder ofte en kvadratrod, der ikke kan forenkles til et heltal. Hvis dette er tilfældet, lad højden være kvadratroden i enkleste form at stå. Her er et eksempel:







Metode 2 af 2: Brug af trigonometri

1. Start med en side og et hjørne. Hvis du er fortrolig med trigonometri, så kan du finde arealet af en ligebenet trekant, selvom ingen af længderne af dens sider er kendt. Her er et eksempel på et problem, hvor kun følgende er kendt:
- Længden s af de to lige store sider er 10 cm.
- Vinklen θ mellem de to lige store sider er 120 grader.

2. Del den ligebenede trekant i to retvinklede trekanter. Tegn en linje ned fra toppunktet mellem de to lige store sider, der skærer basen i en ret vinkel. Du har nu to lige retvinklede trekanter.

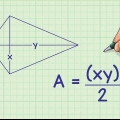
3. Brug trigonometri til at bestemme værdien af h. Nu hvor du har en retvinklet trekant, kan du anvende de trigonometriske funktioner (sinus, cosinus og tangens). I eksempelopgaven ved du hvad hypotenusen er, og du vil have værdien af h kender, siden ved siden af den kendte vinkel. Brug det faktum, at cosinus = tilstødende / hypotenusen til h at løse:

4. Bestem værdien af den resterende side. Der er en endnu ukendt side af den retvinklede trekant, som du x kan navngive. Løs dette med definitionen sinus = modsat / hypotenusen:

5. Brug forholdet mellem x og bunden af den ligebenede trekant. Du kan nu `zoome ud` til den pågældende ligebenede trekant. Basen b af denne vinkel er lig med 2x, da det var opdelt i to segmenter, hver med en længde x.

6. Brug værdierne h og b i arealformlen for trekanten. Nu hvor du kender basen og højden, kan du anvende standardformlen A = ½bh:





7. Omskriv dette som en universel formel. Nu hvor du ved, hvordan du løser dette, kan du anvende den generelle formel uden at gennemgå hele processen hver gang. Her er, hvad du får, hvis du gentager denne proces uden at bruge specifikke værdier (og forenkle brugen af trigonometriegenskaberne):

Tips
- Hvis du har at gøre med en ligebenet retvinklet trekant (to lige store sider og en vinkel på 90 grader), er det meget nemmere at finde arealet. Bruger du en af de korte sider som underlag, er den anden korte side højden. Nu kan formlen A = ½ b * h simplificeres til ½s, hvor s er længden af en kort side.
- Kvadratrødder har to løsninger, en positiv og en negativ, men du kan ignorere den negative i geometri. For eksempel kan du ikke have en trekant med en `negativ højde`.
- Nogle trigonometriske problemer giver dig andre oplysninger til at starte med, såsom længden af basen og en vinkel (og det faktum, at trekanten er ligebenet). Den grundlæggende strategi forbliver den samme: opdel den ligebenede trekant i retvinklede trekanter og regn dem ud for højden ved hjælp af trigonometriske funktioner.
Artikler om emnet "Beregn arealet af en ligebenet trekant"
Оцените, пожалуйста статью
Populær