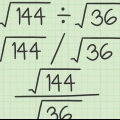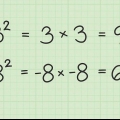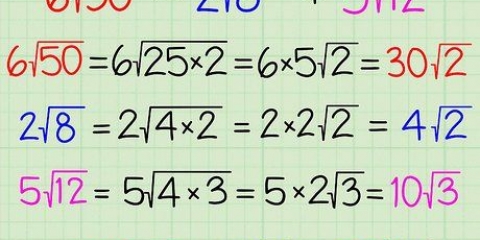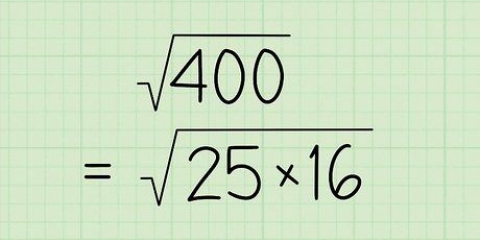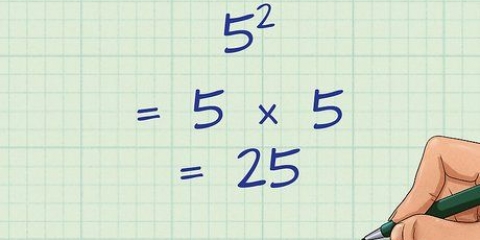Forenkling af kvadratrødder

Indhold

Trin
Tips
Advarsler

At forenkle en kvadratrod er ikke så svært, som det ser ud til. For at forenkle en kvadratrod skal du blot faktorisere antallet af kvadratroden og prøve at tage kvadratroden af en eller begge faktorer. Når du kender nogle almindelige kvadrattal og ved, hvordan man opdeler et tal i faktorer, er du godt på vej til at forenkle en kvadratrod. Sådan kan du hurtigt lære det.

Trin

Metode 1 af 4: Simplificering af kvadratroden af et tal

1. Lær nogle kvadrattal og deres rødder. Kvadring, multiplicering af et tal med sig selv, giver et kvadratisk tal (helt kvadratisk). For eksempel: 25 er et tal i anden kvadrat, fordi 5 x 5 eller 5 er lig med 25. At kende mindst de første 10 ti kvadratiske tal kan hjælpe med at genkende og forenkle kvadratrødder. Her er de første ti kvadratiske tal:

1 = 1
2 = 4
3 = 9
4 = 16
5 = 25
6 = 36
7 = 49
8 = 64
9 = 81
10 = 100

2. Find kvadratroden af et kvadrattal. Hvis du ser et kvadrattal under et radikal, så skal du bare fjerne radikalet (√ ), og skrive kvadratroden af kvadrattallet. Hvis du allerede havde lært dette udenad, så er du færdig. Hvis tallet er for stort, og du ikke er sikker på, om det er et kvadrattal, så prøv at finde kvadratroden med din lommeregner for at kontrollere, om det giver et pænt rundt tal. For eksempel: ved √25 ved du, at svaret er lig med 5, fordi 25 er et tal i anden.

Metode 2 af 4: Simplificering af en kvadratrod ved faktorisering

Billede med titlen Simplify a Square Root Trin 4

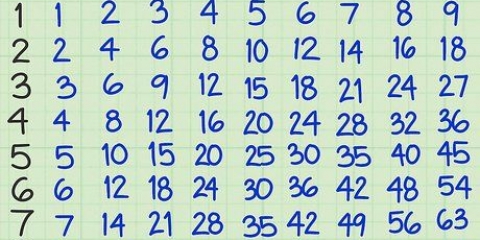
1. Hvis tallet er lige, divideres det med 2. At finde faktorerne for et tal involverer at finde alle tal, der ganges sammen producerer dette tal, hvilket gør det lettere at bestemme dets kvadratrod. Hvis det er et lige tal, så er det første du kan gøre at dividere tallet med 2. I dette eksempel kan du opdele √98 i √(2x49), fordi 98 : 2 =49. Hvis tallet ikke er deleligt med 2, prøv 3, 4, 5 og så videre, indtil du finder den rigtige kombination.

Billede med titlen Simplify a Square Root Trin 5

2. Opdel disse faktorer tilbage i faktorer for at finde yderligere kvadrattal. Se om du kan blive ved med at opdele tallet i faktorer. 2 er primtal og har kun sig selv og 1 som divisor. Men 49, den anden faktor, kan stadig opdeles i 7 x 7, fordi det er et kvadrattal. Så du kan omskrive roden √(2x49) som √(2x7x7), eller √[2(7)], hvilket betyder, at vi allerede har fundet det kvadrattal, vi ledte efter.

Billede med titlen Simplify a Square Root Trin 6

3. Forenkle kvadratroden. Da √98= √[2(7)], er det muligt at placere et 7 uden for radikalet og forenkle svaret til 7√2. Så √49 eller også (7 x 7), bliver så 7, så snart du placerer det uden for radikalen. Hvis du placerer 7`eren tilbage igen, bliver det et kvadrattal igen og derfor 49. Så √98 = 7√2.

Metode 3 af 4: Andre metoder til at forenkle en kvadratrod

1. Hvis det ikke umiddelbart lykkes dig at finde et kvadrattal, så divider tallet yderligere. For eksempel, hvis problemet er √48, fortsætter du med at dividere, indtil du ikke kan gå ud over 2x2, så 4 bliver en koefficient for radikalet og 3 forbliver inde i radikalet. Sådan fungerer det:

√48 = √(2 x 24)
√(2 x 24) = √(2 x 12 x 2)
√(2 x 12 x 2) = √(2 x 6 x 2 x 2)
√(2 x 6 x 2 x 2) = √(2 x 3 x 2 x 2 x 2)
√(2 x 3 x 2 x 2 x 2) = √(2 x 3)
√(2 x 3)= 4√3
√48 = 4√3

2. Husk at du ikke kan forenkle et primtal. Det er fordi faktorerne her er 1 og selve primtallet. For eksempel: √17 kan ikke forenkles, fordi 17 er primtal.

3. Opdeling i faktorer med mere end et kvadrattal. Hvis tallets faktorer indeholder mere end ét kvadrattal, skal du tage dem alle uden for radikalen. Hvis du har fundet flere firkanter, mens du simplificerer, skal du tage dem alle uden for radikalen og gange dem. For eksempel: Lad os antage, at du vil forenkle tallet √32, og opdele det derefter i faktorerne 4 x 4 x 2, idet du bemærker, at kvadrattallet 4 forekommer to gange. Lav denne 16√2, som til sidst vil give 4√2.

4. Forveksle ikke koefficienten med en højere magtrod. 3√125, for eksempel, er lig med 3 x √125, men √125 er terningroden af 125. (fordi 5 x 5 x 5 = 125, √125 = 5.)

Metode 4 af 4: At kende terminologien

1. Husk at radikalet (√) er symbolet for kvadratroden. For eksempel i opgaven √25, "√" det radikale tegn.

2. Husk, at det radikale er tallet under det radikale. Find kvadratroden af dette tal. For eksempel: ved √25 er "25" rodnummeret.

3. Husk at koefficienten er tallet uden for radikalet. Dette tal multiplicerer kvadratroden; Dette kan findes til venstre for det radikale tegn, √-symbolet. For eksempel: ved 7√2, "7" koefficienten.

4. Husk, at en faktor er et tal, der går helt ind i et andet tal. For eksempel: 2 er en faktor på 8, fordi 8 ÷ 4 = 2, men 3 er ikke en faktor på 8, fordi 8÷3 ikke svarer til et heltal. For eksempel: 5 er en faktor på 25, fordi 5 x 5 = 25.

5. Forstå betydningen af at forenkle en kvadratrod. At forenkle en kvadratrod indebærer simpelthen at opdele kvadratroden i faktorer, og derefter flytte den til venstre for radikalen og efterlade den anden faktor inde i radikalen. Hvis tallet er et kvadrattal, kan du fjerne det radikale tegn, så snart du har skrevet dets kvadratrod. For eksempel: √98 kan forenkles til 7√2.

Tips

En måde at finde kvadrater til at dividere dine kvadrattal på er at slå kvadrater op på din liste begyndende med det mindste tal efter dit kvadrattal. For eksempel: hvis du leder efter kvadrattallet 27, så start ved 25 og stop ved 9, fordi du har fundet den største divisor, der er et kvadrattal.

Advarsler

Brug ikke lommeregnere undtagen i det trin, hvor du forsøger at finde ud af, hvor mange gange kvadratet går ind i kvadratroden.
At forenkle er ikke det samme som at sætte værdier i en ligning.Intet sted i hele processen kan et decimaltal optræde nogen steder!