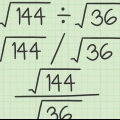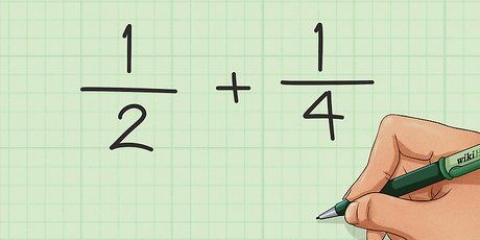Tilføj og fratræk kvadratrødder: 9 trin (med billeder)

Indhold

Trin
- Del 1 af 2: Mestring af det grundlæggende
- Del 2 af 2: Mere motion
Tips
Advarsler

For at tilføje og trække kvadratrødder fra, skal du kombinere kvadratrødder med den samme rod. Det betyder, at du kan tilføje (eller trække fra) 2√3 til 4√3, men du kan ikke tilføje 2√3 og 2√5. Der er mange tilfælde, hvor du kan forenkle tallet under radikalet for at være i stand til at kombinere ens udtryk og frit addere og subtrahere kvadratrødder.

Trin

Del 1 af 2: Mestring af det grundlæggende

1. Forenkle vilkårene under radikalerne, hvis det er muligt. For at forenkle termerne under radikalerne, prøv at indregne dem i mindst én perfekt firkant, såsom 25 (5 x 5) eller 9 (3 x 3). Når du har gjort dette, kan du tage kvadratroden af det perfekte kvadrat og placere det uden for radikalerne, så den resterende faktor efterlades under radikalen. I dette eksempel tager vi udgangspunkt i problemet 6√50 - 2√8 + 5√12. Tallene uden for det radikale er koefficienter og numrene under det kalder vi for rodnumre. Sådan forenkler du vilkårene:

6√50 = 6√(25 x 2) = (6 x 5)√2 = 30√2. Du opløste `50` til `25 x 2` og placerede derefter `5` uden for roden (roden af `25`), hvorefter `2` forbliver under radikalen. Så gange du `5` med `6`, det tal, der allerede var uden for radikalet, og du får 30 som den nye koefficient.
2√8 = 2√(4 x 2) = (2 x 2)√2 = 4√2. Her har du indregnet `8` til `4 x 2` og derefter trukket kvadratroden af 4 fra, så du står tilbage med `2` uden for radikalen og en `2` under radikalen. Så gange du `2` med `2`, det tal, der allerede var uden for radikalet, og du får 4 som den nye koefficient.
5√12 = 5√(4 x 3) = (5 x 2)√3 = 10√3. Her har du indregnet `12` til `4 x 3` og derefter trukket kvadratroden af 4 fra, så du står tilbage med `2` uden for radikalen og en `3` under radikalen. Så gange du `2` med `5`, det tal, der allerede var uden for radikalet, og du får 10 som den nye koefficient.

Billede med titlen Tilføj og fratræk kvadratrødder Trin 2

2. Sæt en cirkel om ethvert led med tilsvarende rodnumre. Når du har forenklet rodnumrene for de givne led, står du tilbage med følgende ligning: 30√2 - 4√2 + 10√3. Da du kun kan tilføje eller trække lignende rødder, skal du sætte en cirkel om disse udtryk med samme rod, i dette eksempel: 30√2 og 4√2. Du kan sammenligne dette med at lægge til eller trække brøker fra, hvor du kun kan addere eller fratrække led, hvis nævnerne er lige store.

Billede med titlen Tilføj og fratræk kvadratrødder Trin 3

3. Hvis du arbejder med en længere ligning, og der er flere par af matchende rodnumre, kan du cirkle om det første par, understrege det andet, stjerne det tredje, og så videre. At sætte ens ord i rækkefølge vil gøre det nemmere for dig at visualisere løsningen.

Billede med titlen Tilføj og fratræk kvadratrødder Trin 4

4. Beregn summen af koefficienterne for led med lige store rødder. Nu skal du bare beregne summen af koefficienterne af led med lige store rødder og ignorere de andre led i ligningen. Rodnumrene forbliver uændrede. Tanken er, at du angiver, hvor mange af den type rodnummer, der er i alt. De uoverensstemmende udtryk kan forblive, som de er. Her er hvad du gør:

30√2 - 4√2 + 10√3 =

(30 - 4)√2 + 10√3 =

26√2 + 10√3

Del 2 af 2: Mere motion

Billede med titlen Tilføj og fratræk kvadratrødder Trin 5

1. Gør eksempel 1. I dette eksempel tilføjer du følgende kvadratrødder: √(45) + 4√5. Du skal gøre følgende:

Forenkle (45). Først kan du frigøre den sådan her √(9 x 5).
Så tager du kvadratroden af ni og du får `3`, som du så placerer uden for kvadratroden. Så, √(45) = 3√5.
Tilføj nu koefficienterne for de to led med matchende rødder for at få dit svar. 3√5 + 4√5 = 7√5

Billede med titlen Tilføj og fratræk kvadratrødder Trin 6

2. Gør eksempel 2. Følgende eksempel er denne opgave: 6√(40) - 3√(10) + √5. Du skal gøre følgende for at rette dette:

Forenkle 6√(40). Først kan du opløse `40` til `4 x 10`, og du får 6√(40) = 6√(4×10).

Derefter beregner du `2` ud fra kvadratet `4`, og du ganger dette med den aktuelle koefficient. Nu har du 6√(4×10) = (6 x 2)√10.

Gang de to koefficienter og du får 12√10`.`

Opgaven lyder nu som følger: 12√10 - 3√(10) + √5. Da de to første led har samme rod, kan du trække det andet led fra det første og lade det tredje være som det er.

du elsker nu (12-3)√10 + √5 om, hvilket kan forenkles til 9√10 + √5.

3. Gør eksempel 3. Dette eksempel lyder sådan her: 9√5 -2√3 - 4√5. Ingen af rødderne indeholder et kvadrat, så ingen forenkling er mulig. Det første og tredje led har lige store rødder, så deres koefficienter kan trækkes fra (9 - 4). Rodnummeret forbliver det samme. De resterende vilkår er ikke ens, så problemet kan forenkles til5√5 - 2√3`.`

Billede med titlen Tilføj og fratræk kvadratrødder Trin 7

Billede med titlen Tilføj og fratræk kvadratrødder Trin 8

4. Gør eksempel 4. Antag, at du har at gøre med følgende problem: √9 + √4 - 3√2 Du skal nu gøre følgende:

Fordi √9 lige med √(3x3), kan du forenkle dette: √9 er ved at blive 3.

Fordi √4 lige med √(2x2), kan du forenkle dette: √4 bliver til 2.

Nu er summen 3 + 2 = 5.

Fordi 5 og 3√2 er ikke lige vilkår, er der ikke mere at gøre nu. Dit endelige svar er 5 - 3√2.

Billede med titlen Tilføj og fratræk kvadratrødder Trin 9

5. Gør eksempel 5. Lad os prøve at tage summen af kvadratrødder, der er en del af en brøk. Ligesom en almindelig brøk, kan du nu kun beregne summen af brøker med samme tæller eller nævner. Lad os sige, at du arbejder med dette problem: (√2)/4 + (√2)/2, Gør nu følgende:

Sørg for, at disse udtryk har samme nævner. Den mindste fællesnævner eller nævner, der kan divideres med både `4` og `2` er `4`.

Så for at gøre det andet led ((√2)/2) med en nævner 4, skal du gange både tælleren og nævneren med 2/2. (√2)/2 x 2/2 = (2√2)/4.

Læg nævneren af brøkerne sammen, mens nævneren holdes den samme. Bare gør, hvad du ville, hvis du tilføjede brøker. (√2)/4 + (2√2)/4 = 3√2)/4`.`