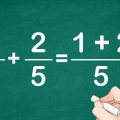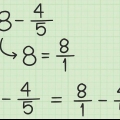du bliver nødt til "at låne" af de 3 tommer "32" for at gøre 2 til 12. Kryds de 3 af "32" og gør det til en 2, så gør enheden 2 til en 12. Nu har du 12 – 7 = 5. Skriv et 5-tal under enhedskolonnen. 



Så i den første sum, 15 - 9, bliver svaret positivt, fordi 15 er større end 9. Så i den anden sum, 2 - 30, bliver svaret negativt, fordi 2 er mindre end 30. 
For opgave 15 - 9, tag 15 mønter. Fjern 9 og tæl hvor mange der er tilbage (6). Så 15 - 9 = 6. Eller brug en tallinje og træk tallene 1 til 15 langs linjen, og streg derefter 9 ud fra 15 og ned for at komme til 6. Med summen 2 – 30 er det nemmere at vende tallene om, og gøre svaret negativt. Så 30 - 2 = 28, og dermed er 2 - 30 -28. 

Glem ikke at inkludere decimaltegnet (kommaet) i svaret. Det ser nu sådan ud: ,2. 




Bemærk, at to tals lcm ikke altid er et af de to tal. For eksempel ved 3 og 2 er LCF 6, fordi der ikke er et tal mindre end 6, som er et multiplum af hvert af tallene. 
Så den nye opgave bliver: 13/10 - 6/10. 









3x - 2x = x -5x - 2x = -7x 2y - y = y -z - 0 = -z 
3x - 5x + 2y - z - (2x + 2x + y) = x - 7x + y - z
Træk tal fra
Indhold
Subtraktioner er de summer, hvor du trækker to tal fra hinanden. Det er ret simpelt, hvis du vil trække hele tal fra hinanden, men det bliver lidt mere kompliceret, når du arbejder med brøker eller decimaler. Når du har mestret subtraktion, kan du gå videre til de mere komplicerede matematiske begreber, og det vil være meget lettere at lægge, gange og dividere tal.
Trin
Metode 1 af 6: Træk store heltal fra ved at låne

1. Skriv det større tal ned. Antag, at du arbejder med summen 32 - 17. Skriv først 32 ned.

2. Skriv det mindste tal direkte under det. Sørg for, at tiere og enere står pænt på linje, så de 3 tommer "32" direkte over 1 tommer "17" tilstand, og de 2 tommer "32" direkte over "7" klokken 17.

3. Træk det nederste tal fra toppen. Dette kan blive en smule vanskeligt, hvis det nederste tal er større end det øverste. I dette tilfælde er 7 større end 2. Her er hvad du skal gøre:

4. Træk de ti i det nederste tal fra de ti i det øverste tal. Glem ikke, at 3 af 32 er blevet til en 2. Træk nu 1 ud af 17 fra 2 over det, så 2-1= 1. Skriv 1 under tierkolonnen. Hvis alt er godt, har du nu 15 som svar, så 32 - 17 = 15.

5. Tjek dit arbejde. Hvis du vil sikre dig, at du har lavet udregningen korrekt, skal du blot tilføje svaret til det mindste tal for at få det største tal tilbage. Så for at tjekke: 15 + 17 = 32, så du gjorde det rigtigt. Fremragende!
Metode 2 af 6: Træk små heltal fra

1. Bestem hvilket tal der er størst. En øvelse som 15 - 9 kræver en anden tilgang end 2 - 30.
- I summen 15 - 9 er det første tal, 15, det største.
- I summen 2 - 30, det andet tal, er 30 det største.

2. Beslut om dit svar skal være positivt eller negativt. Hvis det første tal er det største, så er svaret positivt. Hvis det andet tal er det største, er svaret negativt.

3. Find forskellen mellem de to tal. For at trække to tal fra skal du beregne forskellen mellem dem.
Metode 3 af 6: Subtrahering af decimaler

1. Skriv det største tal over det mindre tal, så decimalerne er justeret. Antag at du har følgende problem: 10.5 - 8.3. Skriv 10,5 over 8,3 på en sådan måde, at kommaerne er over hinanden.
- Hvis du har et problem, hvor det ene tal har flere decimaler end det andet, skal du udfylde det tomme felt med nuller. For eksempel, hvis du har problemet 5.32 - 4.2, kan du omskrive det til 5.32 = 4.20. Dette ændrer ikke på værdien af et tal, men du sørger for, at begge tal lettere kan trækkes fra hinanden.

2. Træk tiendedelene fra hinanden. Subtraktion fra disse tal er det samme som med heltal, bortset fra at du skal være opmærksom på decimaltegnet, justeret og inkluderet i svaret. I dette tilfælde skal du trække 3 fra 5. 5 - 3 = 2, så du skriver en 2`er under 3`eren i 8.3.

3. Træk nu enhederne fra hinanden. Træk nu 8 fra 0. Lån et dusin af 1`eren (ved siden af 0`eren) for at få 10, træk nu 8 fra 10. Du kan også med det samme beregne summen 10 – 8 = 2, uden det mellemliggende trin med lån, fordi det nederste tal ikke har en ti. Skriv svaret under 8.

4. Så det endelige svar bliver 2.2.

5. Tjek dit arbejde. Hvis du vil sikre dig, at du har lavet udregningen korrekt, skal du blot tilføje svaret til det mindste tal for at få det største tal tilbage. 2,2 + 8,3 = 10,5, så du er klar.
Metode 4 af 6: Fratræk af brøker

1. Sæt tællere og nævnere sammen. Antag, at du arbejder med problemet 13/10 - 3/5. Skriv denne opgave, så begge tællere, 13 og 3, og begge nævnere, 10 og 5, er ved siden af hinanden, adskilt af et minustegn. Det giver dig et bedre overblik over problemet og gør det nemmere at finde en løsning.

2. Find det mindste fælles multiplum. Dette er det mindste multiplum af to tal. LCF på 10 og 5 i dette eksempel er 10.

3. Omskriv brøkerne med de samme nævnere. Brøken 13/10 kan forblive uændret, fordi nævneren ikke har ændret sig, men brøken 3/5 bliver lig med 6/10, fordi nævneren går to gange ind i det fælles multiplum af 10. Nu har du udlignet begge brøker. 3/5 er lig med 6/10, men med den forskel, at det nu ikke længere er et problem at trække begge brøker fra hinanden.

4. Træk begge tællere fra hinanden. Så 13 - 6 = 7. Træk ikke nævnerne fra.

5. Placer den nye tæller over den nye nævner (den tidligere beregnede LCF) for det endelige svar. Den nye tæller er 7, og nævneren for begge brøker er 10. Så det endelige svar er 7/10.

6. Tjek dit arbejde. Hvis du vil sikre dig, at du har lavet udregningen korrekt, skal du blot tilføje svaret til det mindste tal for at få det største tal tilbage. Så for at kontrollere: 7/10 + 6/10 = 13/10. Du er nu klar.
Metode 5 af 6: Træk en brøk fra et helt tal

1. Skriv opgaven. Antag, at vi har følgende problem: 5 - 3/4. Bemærk dette.

2. Konverter hele tallet til en brøk med samme nævner som den givne brøk. Lav en brøkdel af de 5 med nævneren 4. Overvej først, at 5 er lig med brøken 5/1. Så gange du både tælleren og nævneren for den nye brøk med 4 for at få to brøker med samme nævner. Dette holder værdien af brøken den samme, men med forskellige tal. Så 5/1 x 4/4 = 20/4.

3. Omskriv opgaven. Dette kan nu skrives som: 20/4 - 3/4.

4. Træk brøkernes tællere fra og hold brøkerne lige. Så 20 - 3 = 17. Så den endelige tæller bliver 17 og nævneren er 4.

5. Så svaret på problemet er 17/4. For at konvertere denne uægte fraktion til en sammensat fraktion skal du dividere 17 med 4 for at få tallet 4 med en resterende del af 1. Svaret ser så således ud: 4 1/4.
Metode 6 af 6: Subtrahering af variable

1. Skriv opgaven. Antag, at du arbejder på følgende problem: 3x - 5x + 2y - z - (2x + 2x + y). Skriv den første ligning over den anden.

2. Træk alle ens udtryk fra hinanden. Når du arbejder med variable, kan du kun trække led med samme variabel fra og med samme kraft. Det betyder, at du kan lave 4x -7x, men ikke 4x -7x. Så du kan opdele denne opgave sådan her:

3. Giv dit endelige svar. Nu hvor du har trukket alle lige vilkår fra, kan du straks give dit endelige svar. Her er svaret:
Tips
- Del større tal i mindre bidder. Tag: 63 - 25.Ingen siger, at du skal trække alle 25 fra på én gang. Du kan først trække 3 fra for at få 60; træk derefter 20 fra for at få 40 og derefter de sidste 2. Resultat: 38. Og nu behøver du ikke låne.
Advarsler
- Hvis du har en blanding af positive og negative tal, bliver tingene meget vanskeligere.Bliv ved med at lede efter artikler, der kan hjælpe dig med dette.
Artikler om emnet "Træk tal fra"
Оцените, пожалуйста статью
Populær