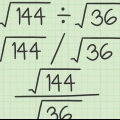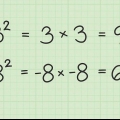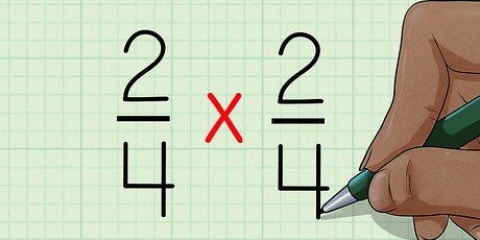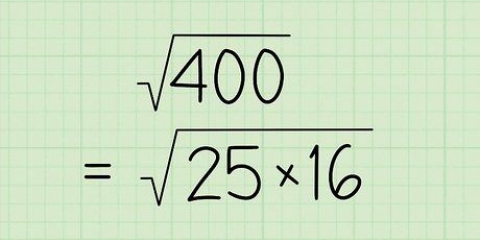Multiplicering af kvadratrødder: 8 trin (med billeder)

Indhold

Trin
- Metode 1 af 2: Multiplicering af kvadratrødder uden koefficienter
- Metode 2 af 2: Multiplicering af kvadratrødder med koefficienter
Tips
Fornødenheder

Ligesom at gange heltal, kan du også gange kvadratrødder (en kvadratrodsligning) sammen. Nogle gange har kvadratrødder koefficienter (et heltal før radikalet), men dette tilføjer bare et trin til multiplikationen og ændrer ikke processen. Den sværeste del af kvadratrodsmultiplikation er at forenkle udtrykket for at få det endelige svar, men selv dette trin er nemt, hvis du kender dine perfekte kvadrater.

Trin

Metode 1 af 2: Multiplicering af kvadratrødder uden koefficienter

1. Multiplicer rødderne sammen. En radicand (engelsk) er et tal under radikalet. Multiplicer rødder på samme måde som heltal. Sørg for, at produktet forbliver under det radikale tegn.

Hvis du fx regner $\sqrt{15} \times \sqrt{5}$ ${sqrt{15}} gange {sqrt{5}}$ , så får du $15 \times 5 = 75$ $15 gange 5=75$ . så, $\sqrt{15} \times \sqrt{5} = \sqrt{75}$ ${sqrt{15}}time {sqrt{5}}={sqrt{75}}$ .

Billede med titlen Multiply Square Roots Trin 2

2. Udled eventuelle perfekte kvadrater fra kvadratroden. Det gør du ved at kontrollere, om et perfekt kvadrat er en faktor af tallet under radikalet. Hvis du ikke er i stand til at udlede et perfekt kvadrat, er dit svar allerede blevet forenklet, og du behøver ikke at gøre andet.

Et perfekt kvadrat er resultatet af at gange et tal (positivt eller negativt heltal) med sig selv. For eksempel: 25 er et perfekt kvadrat, fordi

5 \times 5 = 25

$5gange 5=25$ .

For eksempel,

\sqrt{75}

${sqrt{75}}$ kan indregnes i den perfekte firkant 25:

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25 gange 3}}$

Billede med titlen Multiply Square Roots Trin 3

3. Placer kvadratroden før radikalen. Lad den anden faktor ligge under det radikale. Nu har du det forenklede udtryk.

For eksempel,

\sqrt{75}

${sqrt{75}}$ kan opløses i

\sqrt{25 \times 3}

${sqrt{25 gange 3}}$ , for kvadratroden af 25 (som er 5):

\sqrt{75}

${sqrt{75}}$
=

\sqrt{25 \times 3}

${sqrt{25 gange 3}}$
=

5 \sqrt{3}

$5{sqrt{3}}$

Billede med titlen Multiply Square Roots Trin 4

4. Beregn kvadratet af en kvadratrod. I nogle tilfælde skal du gange en kvadratrod med sig selv. At kvadrere et tal og tage kvadratroden af et tal er modsatte operationer; så de ophæver hinanden. Resultatet af kvadratet af en kvadratrod er simpelthen tallet under radikalet.

For eksempel,

\sqrt{25} \times \sqrt{25} = 25

${sqrt{25}} gange {sqrt{25}}=25$ . Du får dette resultat pga

\sqrt{25} \times \sqrt{25} = 5 \times 5 = 25

${sqrt{25}} gange {sqrt{25}}=5 gange 5=25$ .

Metode 2 af 2: Multiplicering af kvadratrødder med koefficienter

Billede med titlen Multiplicer kvadratrødder Trin 5

1. Multiplicer koefficienterne. En koefficient er et tal for radikalet. Bare ignorer radikalet og tallet under det, og gange de to heltal sammen. Placer deres produkt før den første radikal.

Pas på plus- og minustegn, når du multiplicerer koefficienter. Husk at et negativt tal gange et positivt tal giver et negativt resultat, og et negativt tal gange et negativt tal giver et positivt resultat.
For eksempel ved udregning $3 \sqrt{2} \times 2 \sqrt{6}$ $3{sqrt{2}} gange 2{sqrt{6}}$ , beregn først $3 \times 2 = 6$ $3gange 2=6$ . Nu er opgaven som følger: $6 \sqrt{2} \times \sqrt{6}$ $6{sqrt{2}}gange {sqrt{6}}$ .

Billede med titlen Multiply Square Roots Trin 6

2. Gang tallene under radikalerne. For at gøre dette skal du gange tallene, som om de var heltal. Sørg for, at produktet forbliver under det radikale tegn.

For eksempel for et udsagn som

6 \sqrt{2} \times \sqrt{6}

$6{sqrt{2}}gange {sqrt{6}}$ , udregn produktet af tallene under radikalerne vha

2 \times 6 = 12

$2gange 6=12$ , så det

\sqrt{2} \times \sqrt{6} = \sqrt{12}

${sqrt{2}} gange {sqrt{6}}={sqrt{12}}$ . Opgaven ser nu således ud:

6 \sqrt{12}

$6{sqrt{12}}$ .

Billede med titlen Multiplicer kvadratrødder Trin 7

3. Hvis det er muligt, udregn eventuelle firkanter under det radikale tegn. Du skal gøre dette for at forenkle dit svar. Hvis du ikke kan løse en firkant, er dit svar allerede blevet forenklet, og du kan springe dette trin over.

Et kvadrat er resultatet af at gange et heltal (positivt eller negativt) med sig selv. For eksempel: 4 er en firkant, fordi

2 \times 2 = 4

$2gange 2=4$ .

For eksempel:

\sqrt{12}

${sqrt{12}}$ kan faktoriseres, så kvadratet af 4 placeres før radikalet:

\sqrt{12}

${sqrt{12}}$
=

\sqrt{4 \times 3}

${sqrt{4 gange 3}}$

Billede med titlen Multiply Square Roots Trin 8

4. Gang kvadratroden med koefficienten. Lad den anden faktor ligge under det radikale. Dette giver et forenklet udtryk.

For eksempel,

6 \sqrt{12}

$6{sqrt{12}}$ kan opløses i

6 \sqrt{4 \times 3}

$6{sqrt{4 gange 3}}$ , hvorefter du kan tage kvadratroden af 4 (altså 2), hvorefter du gange dette med 6:

6 \sqrt{12}

$6{sqrt{12}}$
=

6 \sqrt{4 \times 3}

$6{sqrt{4 gange 3}}$
=

6 \times 2 \sqrt{3}

$6gange 2{sqrt{3}}$
=

12 \sqrt{3}

$12{sqrt{3}}$

Tips

Kend dine firkanter, for det gør denne proces meget nemmere!
Følg de sædvanlige regler for tegnet for et tal for at bestemme, om den nye koefficient vil være positiv eller negativ. En positiv koefficient ganget med en negativ koefficient giver et negativt tal. To positive koefficienter ganget sammen eller to negative koefficienter ganget sammen giver et positivt tal.
Alle udtryk under radikalet er altid positive, så du behøver ikke bekymre dig om tegnet, når du multiplicerer tal under et radikal.