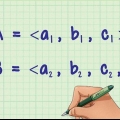Find vinklen mellem to vektorer

Indhold

Trin
Tips

Matematikere og fysikere skal ofte finde vinklen mellem to givne vektorer. Selvom det er let at finde vinklen mellem to vektorer i samme plan ved at tegne grafer, kan det være lidt vanskeligere i rummet eller i tre dimensioner. Denne artikel forklarer den metode, der skal bruges til at finde vinklen mellem to vektorer i planet eller i rummet.

Trin

Metode 1 af 4: Bestem vektorerne

1. Bestem de vektorer, du skal bruge for at finde vinklen. Tag de to vektorer TIL og OQ der skærer hinanden i punktet O, og beregn vinklen MOQ. Du skal bruge vektorerne TIL og OQ brug, lad være MO eller QO. I tilfælde af at MO er kendt, skal du gange det med -1 for at få TIL at få.

Metode 2 af 4: Find det skalære produkt

Find skalarproduktet (eller prikproduktet) af de to vektorer. Hvis du ikke ved, hvordan man beregner skalarproduktet af to vektorer, så læs videre:

1. Bestem vektorens komponenter i hver retning. Når vektorerne er opført i en tabel, repræsenterer den første række normalt x-aksen, den anden række repræsenterer y-aksen og den tredje repræsenterer z-aksen. Hvis vektoren er skrevet på formen xjeg + yj + zk, sæt derefter koefficienterne for jeg, yo, og k størrelsen af komponenterne langs x-, y- og z-akserne (jeg, yo, og k er vektorerne langs x-, y- og z-akserne).

2. Multiplicer komponenterne af begge vektorer langs x-aksen. Gang derefter komponenterne af begge vektorer langs y-aksen og gør det samme for komponenterne langs z-aksen.

3. Læg de tre produkter sammen. Dette er skalarproduktet af begge vektorer. Det skalære produkt, eller "internt produkt", af to vektorer er et meget nyttigt tal i geometri og fysik. I øjeblikket bruger vi kun dette produkt som et værktøj til at beregne vinklen mellem to vektorer. I en todimensional vektor er komponenten langs z-aksen nul, så skalarproduktet kan findes ved kun at betragte komponenterne langs x- og y-aksen.

Metode 3 af 4: Beregn størrelsen

1. Beregn størrelsen af de to vektorer. Beregn størrelsen af de to vektorer ved hjælp af formlen a=b+c+d, hvorved -en er størrelsen af vektoren, og b,c, og d størrelsen af komponenterne i de tre forskellige retninger. I det flade plan d være lig nul.

Metode 4 af 4: = Find vinklen

1. Brug værdierne beregnet ovenfor i denne formel: cosθ = a.b / |a||b|

2. Udled den omvendte cosinus fra dette.

3. Færdig.

Tips

Du kan bruge denne metode til at beregne vinklen i 3D- eller x-y-z-grafer ved at betragte siderne som vektorer og behandle vektoren som frie vektorer.