Beregning med vektorer

Indhold

Trin
Tips

Vektorer er størrelser, der består af en størrelse og en retning (for eksempel: hastighedsvektor eller vektorhastighed, acceleration og forskydning), i modsætning til skalarer, som kun har størrelse (såsom hastighed, afstand og energi). Mens skalarer kan lægges sammen efter deres størrelser (f.eks. 5 kJ + 6 kJ = 11 kJ), er vektorer lidt mere komplicerede at beregne med. Se trin 1 nedenfor for at lære mere om måder at gøre dette på.

Trin

Metode 1 af 3: Tilføjelse og subtraktion af vektorer

1. Udtryk dimensionerne af en vektor ved hjælp af vektornotation. Fordi vektorer har en størrelse og en retning, er det normalt let at opdele dem i deres x-, y- og/eller z-dimensioner. Disse dimensioner er normalt udtrykt i en notation svarende til at beskrive et punkt i et koordinatsystem (f.eks.

Bemærk, at vektorer kan være 1-, 2- eller 3-dimensionelle. Så vektorer kan have en x-komponent, en x- og y-komponent eller en x, y osv.-komponent. Vores eksempel nedenfor handler om 3-dimensionelle vektorer, men processen ligner den for planet eller en linje.

Lad os antage, at vi har to 3-dimensionelle vektorer, vektor A og vektor B. Vi kan skrive disse vektorer i vektornotation som A =

Billede med titlen Tilføj eller fratræk vektorer Trin 2

2. For at tilføje to vektorer sammen skal du tilføje komponenterne. Hvis komponenterne af to vektorer er kendte, så er det muligt at bestemme vektorerne ved at tilføje deres tilsvarende komponenter. Med andre ord, læg x-komponenten af den første vektor til x-komponenten af den anden og gør det samme for y og z. Svarene du får ved at tilføje x-, y- og z-komponenter af de originale vektorer er x-, y- og z-komponenterne i den nye vektor.

Med generelle ord, A+B =

Lad os tilføje de to vektorer A og B. A = <5, 9, -10> og B = <17, -3, -2>. A + B = <5+17, 9+-3, -10+-2>, eller <22, 6, -12>.

Billede med titlen Tilføj eller fratræk vektorer Trin 3

3. For at trække to vektorer fra, trækker du deres komponenter fra. Altså det samme som med addition, men omvendt.Hvis komponenterne i to vektorer er kendte, så er subtrahering af den ene vektor fra den anden ikke mere end at trække komponenterne fra.

Med generelle ord, A-B =

Lad os trække de to vektorer A og B fra. A = <18, 5, 3> og B = <-10, 9, -10>. A - B = <18--10, 5-9, 3--10>, eller <28, -4, 13>.

Metode 2 af 3: Addition og subtraktion ved hjælp af den bageste metode

Billede med titlen Tilføj eller fratræk vektorer Trin 4

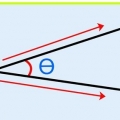
1. Angiv vektorer med en pil. Fordi vektorer har en størrelse og en retning, kan du angive dem med en pil. De har med andre ord en "Udgangspunktet" og en "slutpunkt", peger i vektorens retning, med størrelsen af vektoren angivet med pilen.

Når du tegner en vektor i skala, skal du måle vinklerne omhyggeligt. Forkerte vinkler vil resultere i et forkert svar med denne metode.

Billede med titlen Tilføj eller fratræk vektorer Trin 5

2. Tegn pilene i bagende rækkefølge. Pilens hoved placeres mod halen af den næste pil. Da du kun tilføjer to vektorer, er dette alt hvad du skal gøre for at finde den resulterende vektor.

Bemærk at rækkefølgen du tegner vektorerne i ikke er vigtig, så længe vi antager at du altid bruger det samme udgangspunkt. Vektor A + Vektor B = Vektor B + Vektor A

Billede med titlen Tilføj eller fratræk vektorer Trin 6

3. For at trække fra lav vektoren "negativ". At trække vektorer fra med denne visuelle metode er relativt let. Vend vektorens retning, men hold størrelsen den samme, og tilføj den ved at bruge hoved-til-hale-metoden som normalt. Med andre ord, for at trække en vektor fra, roterer du vektoren 180 og adderer.

Billede med titlen Tilføj eller fratræk vektorer Trin 7

4. Hvis du vil tilføje eller fratrække mere end to vektorer, så sammenkæde alle disse vektorer efter hinanden ved hjælp af den bageste metode. Rækkefølgen er ligegyldig. Du kan bruge dette til et hvilket som helst antal vektorer.

5. Tegn en ny vektor fra halen af den første vektor til hovedet af den sidste. Uanset om du arbejder med 2 eller 100 vektorer, er vektoren, der strækker sig fra startpunktet (halen af din første vektor) til slutpunktet af de tilføjede vektorer (hovedet af din sidste vektor) den resulterende vektor eller summen af alle vektorer. Bemærk, at denne vektor er lig med vektoren opnået ved at tilføje x-, y- og/eller z-komponenterne af alle vektorer.

Billede med titlen Tilføj eller fratræk vektorer Trin 8

Da du har tegnet alle vektorer i skala og målt vinklerne nøjagtigt, kan du finde størrelsen af den resulterende vektor ved at måle længden. Du kan også måle vinklen, som denne resultant laver med en specifik vektor eller med den vandrette/lodrette osv. at finde retningen.

Da du ikke har tegnet alle vektorer i skala, bliver du sandsynligvis nødt til at beregne størrelsen af resultanten ved hjælp af trigonometri. Brug sinus- eller cosinusreglen til dette. Da du tilføjer mere end to vektorer, er det nyttigt at tilføje to af dem først og derefter tilføje deres resultant til den tredje vektor, og så videre. Se næste afsnit for mere information.

Billede med titlen Tilføj eller fratræk vektorer Trin 9

6. Vis den resulterende vektor efter størrelse og retning. Vektorer bestemmes af deres længde og retning. Som nævnt ovenfor, forudsat at du har tegnet vektorerne nøjagtigt, er størrelsen af vektoren lig med dens længde og retning, og dens vinkel er i forhold til lodret, vandret osv. Brug enhederne for de vektorer, du har lagt sammen, til at vælge enhederne for størrelsen af den resulterende vektor.

For eksempel, hvis vektorerne vi tilføjede repræsenterer en hastighedsvektor i ms, så kunne vi repræsentere den resulterende vektor som "en hastighedsvektor på x ms kl y i forhold til vandret".

Metode 3 af 3: Addere og subtrahere vektorer ved at bestemme komponenterne

Billede med titlen Tilføj eller fratræk vektorer Trin 10

1. Brug trigonometri til at finde vektorens komponenter. Du har brug for størrelsen og retningen i forhold til vandret eller lodret, og du skal have noget praktisk kendskab til trigonometri. Antag, at vi har en 2-D vektor. Først gør du vektorerne til hypotenusen af en retvinklet trekant, med de to andre sider parallelle med x- og y-akserne. Du kan tænke på disse to sider som hoved-til-hale vektorer, der, når de lægges sammen, giver den originale vektor.

Længderne af de to sider er lig med størrelserne af x- og y-komponenterne i din vektor og kan beregnes ved hjælp af trigonometri. Hvis x er størrelsen af vektoren, så er den side, der støder op til vektorens vinkel (i forhold til vandret, lodret osv.) svarende til xcos(θ), mens det modsatte er lig med xsin(θ).
Det er også vigtigt at overveje orienteringen af dine komponenter. Hvis komponenten peger i negativ retning af en af akserne, får den et minustegn. For eksempel, hvis en komponent peger til venstre eller til bunden i planet, får den et minustegn.
Lad os f.eks. sige, at vi har en vektor med størrelsesorden 3 og en retning 135 i forhold til vandret. Med denne information kan vi bestemme, at x-komponenten er lig med 3cos(135) = -2.12 og y-komponenten er 3sin(135) = 2.12

Billede med titlen Tilføj eller fratræk vektorer Trin 11

2. Læg de tilsvarende komponenter af to eller flere vektorer sammen. Når du har fundet komponenterne af alle vektorerne, skal du blot lægge størrelserne sammen for at finde komponenterne i din resulterende vektor. Læg først størrelserne på de vandrette komponenter sammen (parallelt med x-aksen). Tilføj derefter størrelserne på de lodrette komponenter (parallelt med y-aksen). Hvis en komponent har et minustegn (-) foran sig, trækkes dens størrelse fra. De svar, du får, er komponenterne i din resulterende vektor.

For eksempel tager vi vektoren fra det forrige trin, <-2.12 og 2.12>, og føj det til vektoren <5,78 og -9>. I dette tilfælde er vores resulterende vektor <-2,12+5.78 og 2,12-9>, eller <3,66 og -6,88>.

Billede med titlen Tilføj eller fratræk vektorer Trin 12

3. Beregn størrelsen af den resulterende vektor ved hjælp af Pythagoras sætning. Med denne udtalelse, c=a+b, kan du finde længden af siderne i retvinklede trekanter?. Da trekanten dannet af den resulterende vektor og dens komponenter er en retvinklet trekant, kan vi bruge denne sætning til at finde vektorens længde og dermed dens størrelse. Af c som størrelsen af den resulterende vektor, du forsøger at finde, f.eks -en ind som størrelsen af x-komponenten og b som størrelsen af y-komponenten. Løs med algebra.

For at finde størrelsen af vektoren, hvis komponenter vi bestemte i det foregående trin, <3,66 og -6,88>, vi bruger Pythagoras sætning. Løs som følger:

c=(3,66)+(-6,88)

c=13,40+47,33

c=√60,73 = 7,79

Billede med titlen Tilføj eller fratræk vektorer Trin 13

4. Beregn retningen af resultanten med tangenten. Til sidst bestemmer vi retningen af den resulterende vektor. Brug formlen θ=tan(b/a), hvor θ er den vinkel resultanten laver med x-aksen fra vandret, hvor b er størrelsen af y-komponenten og a er størrelsen af x-komponenten.

For at bestemme retningen af vores eksempelvektor bruger vi θ=tan(b/a).

θ=tan(-6.88/3.66)

θ=tan(-1.88)

θ=-61.99

Billede med titlen Tilføj eller fratræk vektorer Trin 14

5. Vis den resulterende vektor efter størrelse og retning. Som angivet ovenfor er vektorer defineret ved deres størrelse og retning. Sørg for at bruge de korrekte enheder til vektorstørrelsen.

For eksempel, hvis eksempelvektoren repræsenterer en kraft (i Newton), kan vi skrive dette som "en kraft af 7,79 Ikke -61,99 fra vandret".

Tips

Vektorer må ikke forveksles med størrelser.
Du kan finde størrelsen af en vektor i rummet ved formlen a=b+c+d at bruge, hvor -en er størrelsen af vektoren og b, c og d komponenterne i hver retning.
Vektorer repræsenteret som xjeg + yj + zk kan adderes eller subtraheres ved blot at addere eller subtrahere koefficienterne for de tre vektorer. Svaret er da også på formen i, j, k.
Kolonnevektorer kan tilføjes og trækkes fra ved at tilføje eller trække værdierne i hver række.