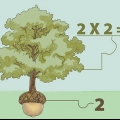
Eks. 2 x 32 = 64. 
Eks. √64 = 8. 






Eks. 2,878521796 / 3 = 0,959507265… 
Eks. invers log 0,959507265 = 9,109766916. Så den geometriske middelværdi af 7, 9 og 12 er lig med 9.11. Det geometriske middelværdi af ethvert sæt tal er altid mindre end eller lig med det aritmetiske middelværdi af dette sæt. Det geometriske middelværdi gælder kun for positive tal. I opgaver, hvor der spørges til beregningen af det geometriske middelværdi, giver det normalt ikke meget mening at arbejde med negative tal.
Beregning af den geometriske middelværdi
Indhold
Det geometriske middel er et matematisk udtryk relateret til og ofte forvekslet med det mere almindeligt anvendte aritmetiske middel. For at beregne det geometriske middelværdi bruger vi en af nedenstående metoder.
Trin
Metode 1 af 4: To tal: nem metode

1. Bestem hvilke tal du vil beregne gennemsnittet af.
- Eks. 2 og 32.

2. Multiplicer dem sammen.

3. Beregn kvadratroden af det resulterende produkt.
Metode 2 af 4: To tal: detaljeret metode

1. Begynd at udfylde tallene i ligningen nedenfor. For eksempel, hvis du arbejder med tallene 10 og 15, skal du indtaste 10 og 15 som vist nedenfor.

2. Løs for x. Start krydsmultiplikation. Da x*x = x, vil din ligning se sådan ud: x = (produkt af de to andre tal). For at løse for x skal du finde kvadratroden af dette produkt. Med lidt held vil dette komme ud med et heltal. Hvis dette ikke er tilfældet, angiv tallet i decimaler, eller lad kvadratroden stå, afhængigt af kravene. Det angivne eksempel er i form af en kvadratrod.
Metode 3 af 4: Tre eller flere tal: Simpel metode

1. Indsæt dine tal i ligningen nedenfor. Middel = (a1 × a2 ×. . .× an)
- -en1 er dit første nummer og et2 er det andet tal og så videre
- n er antallet af tal

2. Gang tallene a1, -en2, etc. med hinanden.

3. Beregn nrod af dette tal. Dette er den geometriske middelværdi.
Metode 4 af 4: Tre eller flere tal: Logaritmer

1. Find loggen for hvert tal og læg disse værdier sammen. Find knappen LOG på din lommeregner. Skriv nu: (første tal) LOG + (andet tal) LOG + (tredje tal) LOG [+ log af følgende tal, hvis nogen] =. Glem ikke at tjekke = ellers vil du kun se loggen for det sidste tal, ikke totalen.
- Eks. log 7 + log 9 + log 12 = 2,878521796..

2. Divider summen af de logaritmiske værdier med antallet af tal, du har lagt sammen. Når du har lagt logfilerne for de tre tal sammen, skal du dividere med tre.

3. Find det omvendte af resultatets log. Hvordan dette virker på en lommeregner afhænger af producenten, men alle gode har en omvendt funktion. Se din manual for at finde ud af, hvor den er placeret. Den omvendte log i dette tilfælde er den geometriske middelværdi.
Tips
- Forskellen mellem det aritmetiske og geometriske middelværdi:
- hvis du aritmetisk middelværdi hvis du vil beregne 3, 4 og 18, så gør 3 + 4 + 18 og divider denne sum med 3 (fordi der er tre tal). Så 25/3 = 8,333.... Den aritmetiske middelværdi besvarer spørgsmålet, "Hvis alle tal er ens, hvad skulle disse tal så være for at summere til den samme total??"
- Det geometrisk middelværdi svarer rigtigt på spørgsmålet, "Hvis alle tal har samme størrelse, hvad skulle disse tal så være for at gange for at få den samme total??" Så for at finde den geometriske middelværdi af 3, 4 og 18, ville vi gøre 3 x 4 x 18 = 216. Så tager vi terningroden af dette (fordi der er tre tal). Svaret er 6. Med andre ord, da 6 x 6 x 6 = 3 x 4 x 18, er 6 det geometriske middelværdi af 3, 4 og 18.
Artikler om emnet "Beregning af den geometriske middelværdi"
Оцените, пожалуйста статью
Lignende
Populær