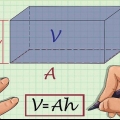
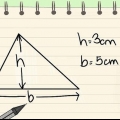
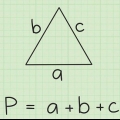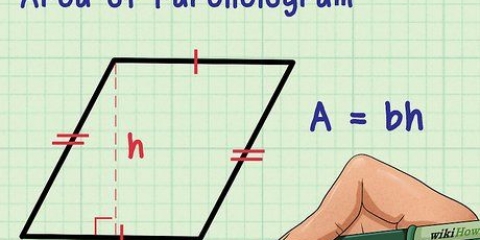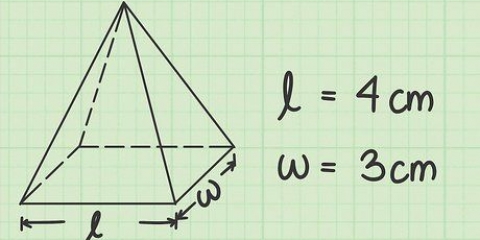Enhver side af trekanten kan være basis, uanset hvordan trekanten er tegnet. For at forestille dig dette, drej trekanten i dit sind, indtil den alt for velkendte side er blevet bunden. For eksempel, hvis du ved, at arealet af en trekant er 20, og en af dens sider er 4, så: A = 20 og b = 4. 
I eksemplet: 20 = 1/2(4)t 20 = 2 timer 10 = h 

Så i eksemplet:c = 8 og a = 4. 
4 + b = 8 16 + b = 64 b = 48 
b = Sqrt (48) = 6,93
Beregning af højden af en trekant
Indhold
For at beregne arealet af en trekant skal du bruge dens højde. Hvis disse oplysninger ikke er givet, kan du nemt beregne det ud fra, hvad du ved! Denne artikel vil lære dig to forskellige måder at finde højden af en trekant på, afhængigt af hvilken information du har fået.
Trin
Metode 1 af 2: Bestemmelse af højden, når areal og bund er kendt

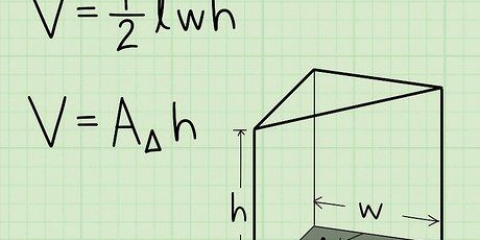
1. Formlen for arealet af en trekant. Dette erA=1/2bh.
- -en = Areal af trekanten
- b = Længden af trekantens basis
- h = Højden af trekantens basis

2. Kig på trekanten og afgør, hvilke variable der er kendt. I dette tilfælde kender du allerede området, så -en er lig med denne værdi.Du bør også kende værdien af en af siderne; angive denne værdi "`b`".Hvis du ikke kender begge værdier eller en af dem, har du brug for en anden metode.

3. Brug dine værdier i ligningenA=1/2bh og beregne. Gang først grundtallet (b) med 1/2, divider derefter arealet (A) med produktet.Den resulterende værdi er højden af din trekant!
Metode 2 af 2: Find højden af en ligesidet trekant

1. Egenskaberne for en ligesidet trekant. En ligesidet trekant har tre lige store sider og tre lige store vinkler på hver 60 grader. Hvis du deler en ligesidet trekant i to, ender du med to kongruente retvinklede trekanter.
- I dette eksempel vil vi bruge en ligesidet trekant med sider, der har en længde på 8.
2. Pythagoras sætning. Pythagoras sætning siger, at for en retvinklet trekant med sider af længde -en og b, og en hypotenus af længde c: a + b = c.Vi kan bruge denne sætning til at finde højden af vores ligesidede trekant!

3. Del den ligesidede trekant i to, og tildel værdier til variablerne-en, b ogc.Side -en er lig med halvdelen af længden af en side og side b er højden af trekanten vi vil løse.

4. Udfyld værdierne i Pythagoras sætning og løs for b. Beregn først kvadratet af c og -en ved at gange det med sig selv. Træk derefter a fra c.

5. Find kvadratroden af b for at finde højden af trekanten! Brug kvadratroden på din lommeregner til at finde Sqrt(. Svaret er højden af din ligesidede trekant!
Artikler om emnet "Beregning af højden af en trekant"
Оцените, пожалуйста статью
Lignende
Populær