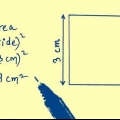
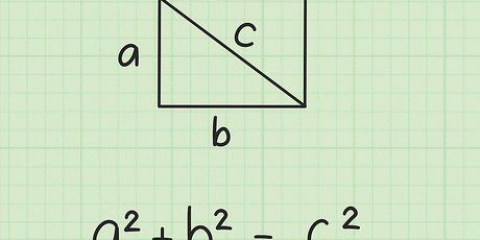
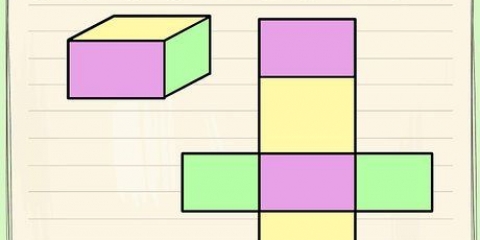
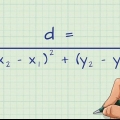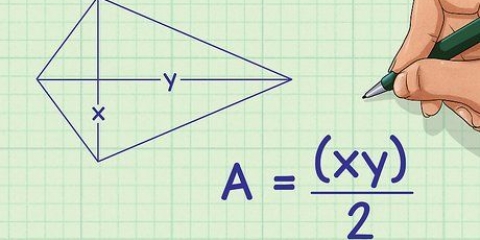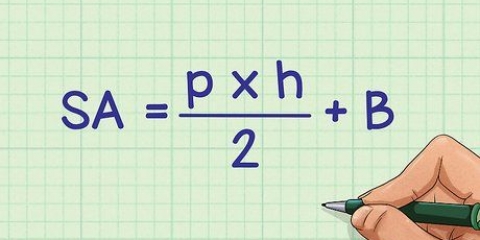De to kortere sider af trekanten er siderne af firkanten: hver har en længde s. Hypotenusen er kvadratets diagonal, d. 


Forenkle: 
Divider begge sider med to: 
Areal = 
Areal = 

Antag for eksempel, at en firkant har en diagonal på 10 cm. Areal = 
=
= 50 cm. For eksempel har en firkant med en diagonal på 10 cm sider af længde  cm.
cm. Hvis du vil finde både længden af en side og arealet af diagonalen, kan du først bruge denne formel og derefter kvadrere svaret for arealet: Areal  cm. Dette er noget mindre præcist, pga
cm. Dette er noget mindre præcist, pga  er et irrationelt tal, der kan have afrundingsfejl.
er et irrationelt tal, der kan have afrundingsfejl. Tegn en firkant på papir. Sørg for, at alle sider er lige. Mål diagonalen. Tegn en anden firkant med den længde som siderne af firkanten. Spor en kopi af din første firkant, så du har to. Klip alle tre firkanter ud. Skær de to mindre firkanter i former, der passer inde i den store firkant. De skal fylde rummet perfekt for at vise, at arealet af den store firkant er nøjagtigt dobbelt så stor som arealet af den mindre firkant.
Beregning af arealet af en firkant ved hjælp af diagonalen
Den mest almindelige formel for arealet af en firkant er enkel: det er længden af en af dens sider i kvadrat, eller s. Men nogle gange kender man kun længden af diagonalen af en firkant, linjen mellem to modstående hjørner. Hvis du er fortrolig med retvinklede trekanter, kan du udlede en ny formel med diagonalen som eneste variabel.
Trin
Del 1 af 2: Beregning af arealet af et kvadrat

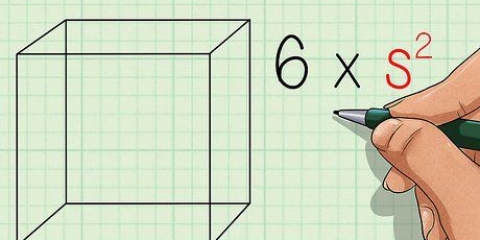
1. Tegn din firkant. Et kvadrat har fire lige store sider. Lad os sige, at hver side har en længde på `s`.

2. Brug standardformlen for arealet af en firkant. Arealet af en firkant er lig med dens længde gange dens bredde. Fordi hver side s det bliver til formel Areal = s x s = s. Dette vil snart vise sig at være nyttigt.

3. Forbind to modstående hjørner for at lave en diagonal. Målingen af denne diagonal bliver d enheder. Denne diagonal deler firkanten i to rette trekanter.

4.Brug Pythagoras sætning til en af trekanterne. Pythagoras sætning er en formel til at finde hypotenusen (længste side) af en retvinklet trekant: (side A) + (side B) = (hypotenusen) eller  . Nu hvor firkanten er delt i to, kan du bruge denne formel på en af de rette trekanter:
. Nu hvor firkanten er delt i to, kan du bruge denne formel på en af de rette trekanter:
 . Nu hvor firkanten er delt i to, kan du bruge denne formel på en af de rette trekanter:
. Nu hvor firkanten er delt i to, kan du bruge denne formel på en af de rette trekanter:

5. Arranger ligningen, så s er på den ene side. Husk, at vi ved, at pladsens areal er s. Hvis du kan isolere s på den ene side, så har du en ny ligning for området:






6. Brug denne formel med et eksempel på et kvadrat. Disse trin har bevist, at formlen Area =  gælder for alle felter. Indtast længden af diagonalen for d og løse.
gælder for alle felter. Indtast længden af diagonalen for d og løse.
 gælder for alle felter. Indtast længden af diagonalen for d og løse.
gælder for alle felter. Indtast længden af diagonalen for d og løse.
=

= 50 cm.
Del 2 af 2: Yderligere info
1. Find diagonalen af længden af en side. Pythagoras sætning for et kvadrat med side s og diagonal d give dig formlen  på. Løs for `d`, hvis du kender længderne af siderne og vil bestemme længden af diagonalen:
på. Løs for `d`, hvis du kender længderne af siderne og vil bestemme længden af diagonalen:
 på. Løs for `d`, hvis du kender længderne af siderne og vil bestemme længden af diagonalen:
på. Løs for `d`, hvis du kender længderne af siderne og vil bestemme længden af diagonalen: - For eksempel, hvis en firkant har sider på 7 cm, så er diagonalen d = 7√2 cm eller omkring 9,9 cm.
- Hvis du ikke har en lommeregner, kan du bruge 1,4 som et estimat på √2.
2. Bestem længden af en side ved hjælp af diagonalen. Er diagonalen givet, og du ved, at diagonalen af et kvadrat  så kan du dividere begge sider med
så kan du dividere begge sider med  til
til  at få.
at få.
 så kan du dividere begge sider med
så kan du dividere begge sider med  til
til  at få.
at få. cm.
cm. cm. Dette er noget mindre præcist, pga
cm. Dette er noget mindre præcist, pga  er et irrationelt tal, der kan have afrundingsfejl.
er et irrationelt tal, der kan have afrundingsfejl.3. Fortolk overfladeformlen. Formlen Areal =  ser ud til at være matematisk korrekt, men er der en måde at teste dette direkte på? Godt,
ser ud til at være matematisk korrekt, men er der en måde at teste dette direkte på? Godt,  er arealet af et andet kvadrat med diagonalen som side. Fordi den fulde formel
er arealet af et andet kvadrat med diagonalen som side. Fordi den fulde formel  du kan ræsonnere, at denne anden firkant har præcis det dobbelte af arealet af den oprindelige firkant. Du kan selv teste dette:
du kan ræsonnere, at denne anden firkant har præcis det dobbelte af arealet af den oprindelige firkant. Du kan selv teste dette:
 ser ud til at være matematisk korrekt, men er der en måde at teste dette direkte på? Godt,
ser ud til at være matematisk korrekt, men er der en måde at teste dette direkte på? Godt,  er arealet af et andet kvadrat med diagonalen som side. Fordi den fulde formel
er arealet af et andet kvadrat med diagonalen som side. Fordi den fulde formel  du kan ræsonnere, at denne anden firkant har præcis det dobbelte af arealet af den oprindelige firkant. Du kan selv teste dette:
du kan ræsonnere, at denne anden firkant har præcis det dobbelte af arealet af den oprindelige firkant. Du kan selv teste dette:Tips
- Denne enkle ligning bruges på mange områder, herunder krystallografi, kemi og kunst. For eksempel kan du bruge det til at beregne arealet af et landskab, du ser under opmåling, eller når du bruger perspektiv i fotografering eller maleri, ved at måle den afstand, du har gået, og forestille dig et gitter af denne afstand som diagonalen.
- Hvis du vil have en mere visuel tilgang til matematik, eller lære at bruge grafer og diagrammer i kunst, eller udforske en partikels spiralsti, så tjek nogle artikler om Microsoft Excel, matematik, regneark og grafik.
- Hvis du ikke har en lommeregner, men har brug for et mere præcist skøn over kvadratroden af to, er der måder at at gøre dette i hånden. Et eksempel på dette er Newton-Raphson-metoden.
Artikler om emnet "Beregning af arealet af en firkant ved hjælp af diagonalen"
Оцените, пожалуйста статью
Lignende
Populær