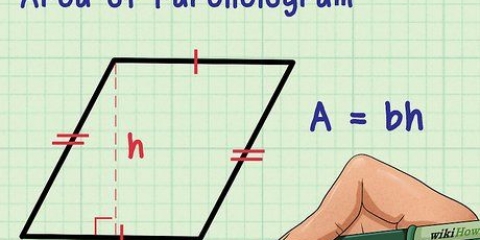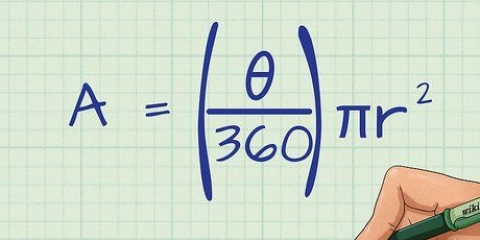Sådan beregnes arealet af en firkant

Indhold

Trin

Så til dit hjemmearbejde skal du beregne arealet af en firkant...men du har ikke engang en anelse om, hvad en firkant er. Gå ikke i panik - redningen er nær! En firkant er enhver figur, der består af 4 sider/vinkler. Alt du skal gøre er at bestemme den firkantede type af problemet og bruge den tilsvarende formel til at beregne arealet.

Trin

Metode 1 af 4: Firkanter, rektangler og andre parallelogrammer

1. Lær, hvordan du bestemmer, hvad et parallelogram er. Et parallelogram er enhver firkant med 2 par parallelle sider, hvor de parallelle sider er lige lange. Firkanter, rektangler og romber er alle parallelogrammer.

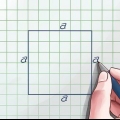
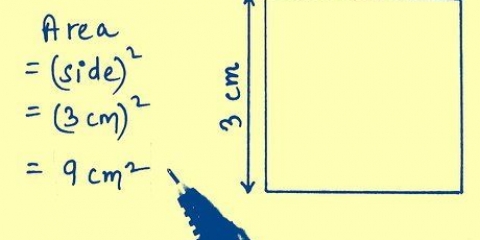
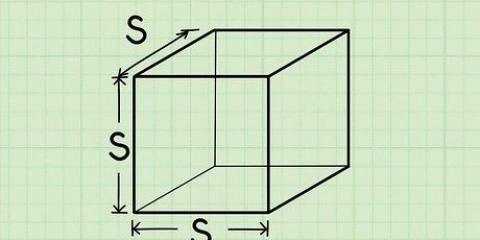
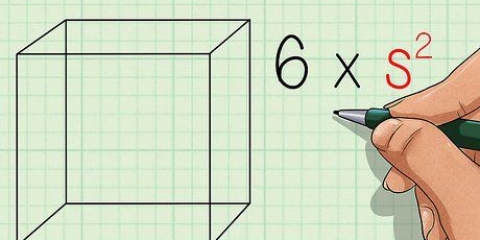
2. Find arealet af en firkant. Da hver side af en firkant er lige lang, skal du blot måle længden af 1 side (kald det "t"), for at finde arealet af en firkant. Dette er det samme som at gange kvadratets grundflade med dets højde; basen og højden er altid ens. Brug følgende formel:

K = t

Dette er det samme som K = t * t

Hvis en side af et kvadrat har en længde på 4, (t = 4), så er arealet t, eller 4 x 4 = 16.

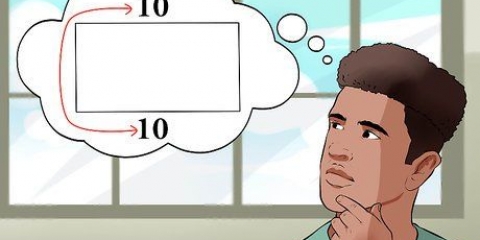
3. Find arealet af et rektangel. For at finde arealet af et rektangel er det nødvendigt at kende længden og bredden af rektanglet. Formlen er som følger:

K = b*h

Hvis længden er længde 10 og bredden er 5, så er arealet af rektanglet 10 x 5 (l * w) = 50.

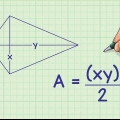
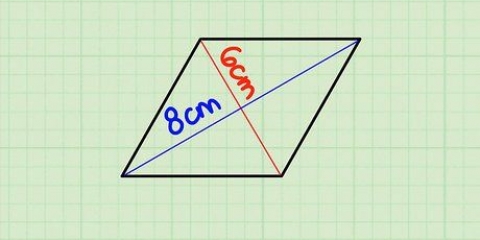
4. Find arealet af en firkant. Dette kan være vanskeligt - du kan ikke bare gange den ene side med den anden her. Du bliver nu nødt til at tegne linjer fra hvert punkt og måle diagonalerne af formen, hvis ikke givet. Derefter ganges diagonalerne sådan her:

K = (b*h)/2, hvor b = diagonal 1 og h = diagonal 2

Hvis et kvadrat har diagonaler med længden 6 og derefter 8, så er arealet (6 x 8)/2 = 48/2 = 24

Metode 2 af 4: Arealet af en trapez

1. Bestem, om det er en trapez. Et trapez er en firkant med mindst 2 sider, der er parallelle. Hver af de fire sider af en trapez kan have forskellig længde. Der er to forskellige måder at finde arealet af en trapez, afhængigt af den givne information.

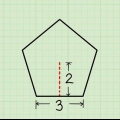
2. Bestem højden af trapez. Højden af en trapez er den vinkelrette linje, der forbinder den øverste basislinje og den nederste basislinje, og du skal bruge dem begge til at beregne arealet. Dette er ikke af samme længde som en af siderne, fordi hver side er diagonal. Sådan finder du højden:

Bestem, hvad det korteste grundlag er. Placer din blyant i hjørnet mellem grundlinjen og tegn en linje lige op eller ned til den anden grundlinje. Du skulle nu have tegnet en trekant med en vinkel på 90 grader.

Brug trigonometri til at bestemme højden. For eksempel, hvis du kender længden af en side og den tilstødende vinkel er kendt, og der er en 90 graders vinkel i trekanten, så er højden længden af siden gange vinklens sinus.

Antag, at højden af trapez er 10.

3. Bestem arealet af trapez ved hjælp af højden og længden af basen. Hvis du kender højden af trapezoidet og længden af begge basissider, skal du bruge følgende formel:

K = (a+b)/2 * h

Hvis højden er 10 og basen har en længde på 7 og 9, så kan du finde arealet ved at beregne: (7 + 9)/2 * 10 = (16/2) * 10 = 8 * 10 = 80

4. Find arealet af en trapez ved hjælp af midtersegmentet. Dette midtersegment er en linje, der løber parallelt med trapezets nedre og øvre linje, og har en længde nøjagtigt imellem. Sådan arbejder du:

Bestem det midterste segment. For at bestemme længden af midtersegmentet m, vi tager gennemsnittet af længderne af siderne -en og b (eller den nedre og øvre linje af trapez).Brug formlen: m = (a+b)/2.Nu hvor du kender længden af midtersegmentet, kan du gange det med højden for at finde arealet. Brug følgende formel:

K = m*h

Dette er i det væsentlige den samme formel som originalen, men erstatter nu "m" udtrykket (a + b)/2.

Antag, at du kender det midterste segment af denne trapez. Antag, at dette er 8, så er arealet af trapezoidet 8 x 10 = 80, ligesom med den forrige metode.

Metode 3 af 4: Bestemmelse af overfladen på en drage

1. Hvad er en drage. En drage er defineret som en geometrisk form, hvor 2 par lige lange sider er forbundet med hinanden, hvilket ligner en almindelig drage. Der er to forskellige måder at finde arealet af denne figur på, afhængigt af den givne information.

2. Find arealet af en drage ved hjælp af længden af dens sider. Hvis du kender længden af to forskellige sider af en drage, og du kender vinklen mellem disse sider, skal du bruge følgende formel, hvor vinklen er lig med theta (θ):

K =(a*b) * sin θ

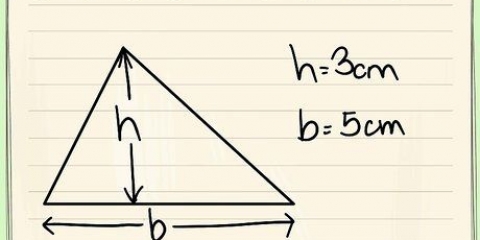
3. Find arealet af en drage ved hjælp af diagonalerne. En diagonal er den lige linje mellem to modstående hjørner af dragen. Hver drage har 2 diagonaler.

Bestem længden af hver diagonal. Tegn en linje fra det ene hjørne af en drage til det modsatte. Du skal nu have 2 trekanter. Bestem vha denne artikel, hvad er længden af diagonalen (de tre vinkler i en trekant summerer til 180 grader).

Når du har bestemt den første diagonal, skal du bruge de samme principper til at bestemme længden af den anden. Brug derefter denne formel til at bestemme området, hvor s og q repræsenterer længden af diagonalerne:

K = (p*q)/2

Hvis diagonalerne har længderne 4 og 6, så kan du finde dragens areal som følger: (4 x 6)/2 = 24/2 = 12

Bemærk, at denne formel også virker for arealet af en rombe, da dette er en speciel slags drage, hvor alle sider er lige lange.

Metode 4 af 4: En generel formel

1. Den generelle formel til bestemmelse af arealet af en firkant. Der er formler til at bestemme arealet af enhver firkant, uanset dens form. Her er den mest generelle form ved hjælp af trigonometriske principper:

hvis k er det samlede areal af firkanten, -en, b, c og d repræsentere længden af de 4 sider, -en er vinklen (i grader) mellem siderne -en og d og C er vinklen (i grader) mellem siderne b og c, derefter:
K = 0.5*a*d * sin A + 0.5*b*c * sin C
Hvis du forsøger at finde arealet af et parallelogram, hvor de modsatte vinkler er ens, bliver formlen enklere: K = 0.5*(ad + bc) * sin A.