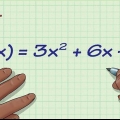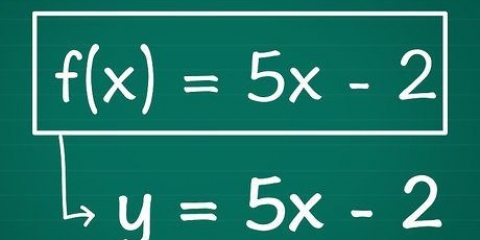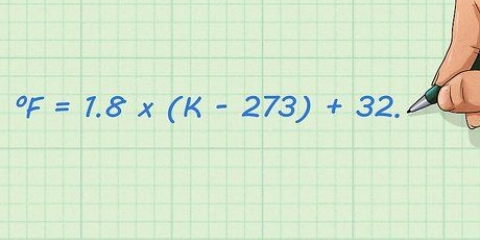er ved at blive
er ved at blive 
 er ved at blive
er ved at blive 
 er ved at blive
er ved at blive  .
.








Hvis de to resultater er ens, så er f(x)=f(-x), og den oprindelige funktion er lige. Et eksempel er:  og
og  .
.Disse to er ens, så funktionen er lige. Hvis hvert led i den nye version af funktionen er det gensidige af det tilsvarende led i originalen, så er f(x)=-f(-x), og funktionen er ulige. For eksempel:  men
men  .
.Bemærk, at hvis du ganger hvert led i den første funktion med -1, laver du den anden funktion. Så den oprindelige funktion g(x) er ulige. Hvis den nye funktion ikke matcher nogen af disse to eksempler, er den hverken lige eller ulige. For eksempel:  men
men  . Det første led er det samme i alle funktioner, men det andet led er en invers. Derfor er denne funktion hverken lige eller ulige.
. Det første led er det samme i alle funktioner, men det andet led er en invers. Derfor er denne funktion hverken lige eller ulige.

Du kan teste for symmetri ved at vælge individuelle punkter. Hvis y-værdien af en x-værdi er den samme som y-værdien af -x, så er funktionen lige. Punkterne valgt ovenfor til plotning  give følgende resultater:
give følgende resultater: (1,3) og (-1,3) (2,9) og (-2,9). De tilsvarende y-værdier for x=1 og x=-1, og for x=2 og x=-2 angiver, at dette er en lige funktion. For en bedre test er valg af to punkter ikke nok bevis, men det er en god indikation. 
Hvis du vælger et par testværdier for x og deres omvendte tilsvarende værdier for -x, bør du få omvendte resultater. Overvej funktionen  . Denne funktion returnerer følgende punkter:
. Denne funktion returnerer følgende punkter:  . Pointen er (1,2).
. Pointen er (1,2). . Pointen er (-1,-2).
. Pointen er (-1,-2). . Pointen er (2,10).
. Pointen er (2,10). . Pointen er (-2,-10).
. Pointen er (-2,-10).Således f(x)=-f(-x), og du kan konkludere, at funktionen er ulige. 
Vælg et par værdier for x og -x som følger:  . Pointen at plotte er (1,4).
. Pointen at plotte er (1,4). . Punktet at plotte er (-1,-2).
. Punktet at plotte er (-1,-2). . Pointen med at plotte er (2,10).
. Pointen med at plotte er (2,10). . Pointen at plotte er (2,-2).
. Pointen at plotte er (2,-2).Dette giver dig allerede point nok til at bemærke, at der ikke er nogen symmetri. Y-værdierne for modsatte par af x-værdier er ikke de samme, og de er heller ikke hinandens omvendte. Denne funktion er hverken lige eller ulige. Du kan muligvis se denne funktion,  , kan omskrives som
, kan omskrives som  . Skrevet i denne form ser det ud som om det er en lige funktion, fordi der kun er én eksponent, og det er et lige tal. Dette eksempel illustrerer dog, at du ikke kan afgøre, om en funktion er lige eller ulige, når den er sat i parentes. Du skal vurdere funktionen i individuelle termer og derefter undersøge eksponenterne.
. Skrevet i denne form ser det ud som om det er en lige funktion, fordi der kun er én eksponent, og det er et lige tal. Dette eksempel illustrerer dog, at du ikke kan afgøre, om en funktion er lige eller ulige, når den er sat i parentes. Du skal vurdere funktionen i individuelle termer og derefter undersøge eksponenterne.
Ved, om en funktion er lige eller ulige
Indhold
En måde at klassificere funktioner på er enten `lige`, `ulige` eller ingen af delene. Disse udtryk refererer til gentagelsen eller symmetrien af funktionen. Den bedste måde at finde ud af det på er ved algebraisk at manipulere funktionen. Du kan også studere grafen for funktionen og se efter symmetri. Når du først ved, hvordan du klassificerer funktioner, kan du også forudsige udseendet af visse kombinationer af funktioner.
Trin
Metode 1 af 2: Test af funktionen algebraisk

1. Se inverse variabler. I algebra er den reciproke af en variabel negativ. Dette er sandt eller variablen af funktionen nu  er eller noget andet. Hvis variablen for den oprindelige funktion allerede er negativ (eller en subtraktion), så er dens gensidige positiv (eller en addition). Følgende er nogle eksempler på variabler og deres inverse:
er eller noget andet. Hvis variablen for den oprindelige funktion allerede er negativ (eller en subtraktion), så er dens gensidige positiv (eller en addition). Følgende er nogle eksempler på variabler og deres inverse:
 er eller noget andet. Hvis variablen for den oprindelige funktion allerede er negativ (eller en subtraktion), så er dens gensidige positiv (eller en addition). Følgende er nogle eksempler på variabler og deres inverse:
er eller noget andet. Hvis variablen for den oprindelige funktion allerede er negativ (eller en subtraktion), så er dens gensidige positiv (eller en addition). Følgende er nogle eksempler på variabler og deres inverse: - Det omvendte af
er
- Det omvendte af
er
- Det omvendte af
er
.

2. Erstat hver variabel i funktionen med dens inverse. Ændre ikke den originale funktion undtagen tegnet. For eksempel:
 er ved at blive
er ved at blive 
 er ved at blive
er ved at blive 
 er ved at blive
er ved at blive  .
.
3. Forenkle den nye funktion. På dette tidspunkt behøver du ikke bekymre dig om at løse funktionen for en given numerisk værdi. Du forenkler bare variablerne for at sammenligne den nye funktion, f(-x), med den oprindelige funktion, f(x). Husk de grundlæggende regler for eksponenter, der siger, at en negativ base til en lige potens vil være positiv, mens en negativ base til en ulige potens vil være negativ.








4. Sammenlign de to funktioner. For hvert eksempel, du prøver, skal du sammenligne den forenklede version af f(-x) med den originale f(x). Sæt vilkårene side om side for nem sammenligning, og sammenlign tegnene på alle vilkår.
 og
og  .
. men
men  .
. men
men  . Det første led er det samme i alle funktioner, men det andet led er en invers. Derfor er denne funktion hverken lige eller ulige.
. Det første led er det samme i alle funktioner, men det andet led er en invers. Derfor er denne funktion hverken lige eller ulige.Metode 2 af 2: Test funktionen grafisk

1. Tegn en graf af funktionen. Brug millimeterpapir eller en grafregner til at tegne funktionen. Vælg forskellige numeriske værdier for  og sæt det i funktionen for at få den resulterende værdi af
og sæt det i funktionen for at få den resulterende værdi af  at beregne. Plot disse punkter på grafen, og efter at have plottet flere punkter tegnes en linje gennem dem for at tegne funktionen.
at beregne. Plot disse punkter på grafen, og efter at have plottet flere punkter tegnes en linje gennem dem for at tegne funktionen.
 og sæt det i funktionen for at få den resulterende værdi af
og sæt det i funktionen for at få den resulterende værdi af  at beregne. Plot disse punkter på grafen, og efter at have plottet flere punkter tegnes en linje gennem dem for at tegne funktionen.
at beregne. Plot disse punkter på grafen, og efter at have plottet flere punkter tegnes en linje gennem dem for at tegne funktionen. - Når du plotter punkterne, skal du være opmærksom på positive og tilsvarende negative værdier for
. For eksempel hvis du har med funktionen at gøre
, så plotter du følgende værdier:
. Dette resulterer i pointen
.
. Dette resulterer i pointen
.
. Dette resulterer i pointen
.
. Dette resulterer i pointen
.

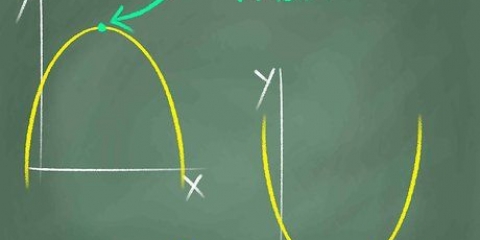
2. Bemærk symmetri langs y-aksen. Når man ser på en funktion, vil symmetri foreslå et spejlbillede. Hvis du ser, at den del af grafen på højre (positive) side af y-aksen matcher den del af grafen på venstre (negative) side af y-aksen, så er grafen symmetrisk om y-aksen. Hvis en funktion er symmetrisk omkring y-aksen, så er funktionen lige.
 give følgende resultater:
give følgende resultater:
3. Test for symmetri fra oprindelsen. Oprindelsen er det centrale punkt (0,0). Oprindelsessymmetri betyder, at et positivt resultat for en valgt x-værdi svarer til et negativt resultat for -x og omvendt. Ulige funktioner udviser oprindelsessymmetri.
 . Denne funktion returnerer følgende punkter:
. Denne funktion returnerer følgende punkter: . Pointen er (1,2).
. Pointen er (1,2). . Pointen er (-1,-2).
. Pointen er (-1,-2). . Pointen er (2,10).
. Pointen er (2,10). . Pointen er (-2,-10).
. Pointen er (-2,-10).
4. Se om der ikke er nogen symmetri. Det sidste eksempel er en funktion uden symmetri på begge sider. Hvis du ser på grafen vil du se, at det ikke er et spejlbillede hverken på y-aksen eller omkring origo. Se funktionen  .
.
 .
. . Pointen at plotte er (1,4).
. Pointen at plotte er (1,4). . Punktet at plotte er (-1,-2).
. Punktet at plotte er (-1,-2). . Pointen med at plotte er (2,10).
. Pointen med at plotte er (2,10). . Pointen at plotte er (2,-2).
. Pointen at plotte er (2,-2). , kan omskrives som
, kan omskrives som  . Skrevet i denne form ser det ud som om det er en lige funktion, fordi der kun er én eksponent, og det er et lige tal. Dette eksempel illustrerer dog, at du ikke kan afgøre, om en funktion er lige eller ulige, når den er sat i parentes. Du skal vurdere funktionen i individuelle termer og derefter undersøge eksponenterne.
. Skrevet i denne form ser det ud som om det er en lige funktion, fordi der kun er én eksponent, og det er et lige tal. Dette eksempel illustrerer dog, at du ikke kan afgøre, om en funktion er lige eller ulige, når den er sat i parentes. Du skal vurdere funktionen i individuelle termer og derefter undersøge eksponenterne.Tips
- Hvis alle former for en variabel i funktionen har lige eksponenter, så er funktionen lige. Hvis alle eksponenter er ulige, er funktionen samlet set ulige.
Advarsel
- Denne artikel gælder kun for funktioner med to variable, som kan tegnes i et todimensionelt koordinatsystem.
Artikler om emnet "Ved, om en funktion er lige eller ulige"
Оцените, пожалуйста статью
Lignende
Populær