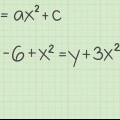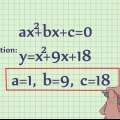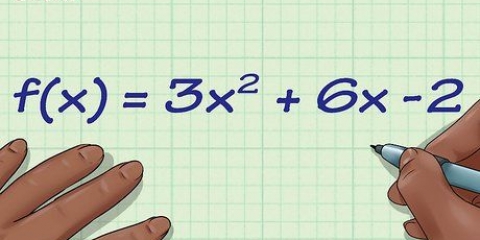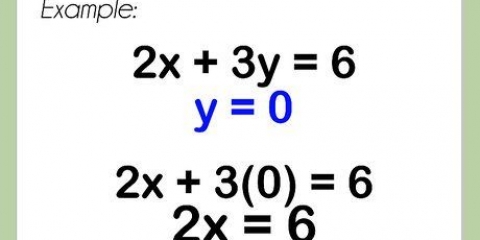Husk, at hver operation på den ene side af lighedstegnet også skal udføres på den anden side. Eksempel: For at fortsætte med vores eksempel tilføjer vi først 2 på begge sider af ligningen. Dette giver os y + 2 = 5x. Så dividerer vi begge sider af ligningen med 5, så (y + 2)/5 = x. Til sidst, for at gøre det mere læsbart, omskriver vi ligningen med "x" til venstre: x = (y + 2)/5. 
Eksempel: Efter at have byttet x og y får vi y = (x + 2)/5 
Fordi x er lig med 1/x, kan du også skrive f(x) som "1/f(x)," en anden notation for det omvendte af f(x). 
Eksempel: Lad os indtaste 4 som værdien af x i vores oprindelige sammenligning. Dette giver os f(x) = 5(4) - 2 eller f(x) = 18. Dernæst skal vi indtaste dette resultat i det omvendte. Så vi erstatter 18 i den inverse funktion som værdien af x. Ved at gøre dette får vi y = (18 + 2)/5 som et resultat, og dette er lig med y = 4. Så 4 er den x-værdi, vi startede med, og med det ved vi, at vi har fundet den rigtige inverse funktion.
Find det omvendte af en funktion
En funktion i matematik (normalt noteret som f(x)) kan opfattes som en slags formel eller program, hvor du indtaster en værdi "x" tucks i, som så returnerer en given værdi for y. Det omvendt af en funktion f(x) (noteret som f(x)) er i det væsentlige det omvendte: indtast a y-værdi, og du får jo tidligere x-værdi tilbage. At finde det omvendte af en funktion kan virke kompliceret, men til simple ligninger behøver du kun en vis viden om de grundlæggende operationer i algebra. Læs følgende trin-for-trin instruktioner og se godt på eksemplet.
Trin

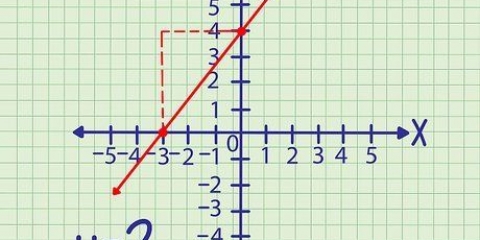
1. Skriv din funktion, skift f(x) med y Hvis det er nødvendigt. Din formel hører hjemme y at have på den ene side af lighedstegnet og på den anden side x-vilkår. Hvis du allerede har en ligning skrevet ind y og x udtryk (som f.eks. 2 + y = 3x), så mangler du bare y løses ved at isolere det.
- Eksempel: Vi har en funktion f(x) = 5x - 2, og omskriver den som y = 5x - 2, simpelthen ved "f(x)" skal erstattes af y.
- Bemærk: f(x) er standardfunktionsnotationen, men hvis du har at gøre med flere funktioner, vil hver funktion få et forskelligt begyndelsesbogstav for at gøre det nemmere at skelne dem. For eksempel er g(x) og h(x) almindeligt anvendte bogstaver til funktioner.

2. løs x på. Med andre ord, lav de nødvendige redigeringer til x at isolere på den ene side af lighedstegnet. For at gøre dette skal du bruge algebras grundlæggende operationer: if x har en koefficient (et tal for variablen), divider begge sider af ligningen med dette tal for at annullere det; er der en konstant inden for "x"-led, og regn det derefter ud ved at addere eller trække begge sider af lighedstegnet, og så videre.

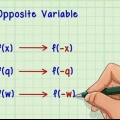
3. Skift variablerne. Bytte rundt x af y og omvendt. Den resulterende ligning er det omvendte af den oprindelige funktion. Med andre ord, hvis vi har en værdi for x udfyld vores oprindelige ligning, så kan vi udfylde svaret i det omvendte (igen for "x"), som returnerer den oprindelige værdi!

4. erstatte y ved hjælp af "f(x)". Inverse funktioner er normalt noteret som f(x) = (x led) . Husk, at i dette tilfælde betyder eksponenten -1 ikke, at vi skal udføre en eksponentiel operation på funktionen. Det er blot en måde at indikere, at denne funktion er det omvendte af originalen.

5. Tjek dit arbejde. Prøv at udfylde en konstant i den oprindelige funktion for x. Hvis du fandt den rigtige inverse, ville du finde den oprindelige værdi af "x" skal se det igen, hvis du indtaster resultatet af dette omvendt.
Tips
- Du kan uden problemer bruge både notationerne f(x) = y og f^(-1)(x) = y, hvis du laver matematiske operationer på funktionerne. Men det er bedre at holde den oprindelige funktion og den omvendte funktion adskilt, så prøv at holde den i fælles notation. I tilfælde af den inverse funktion er notationen f^(-1)(x).
- Bemærk, at det omvendte af en funktion normalt, men ikke altid, er en funktion i sig selv.
Artikler om emnet "Find det omvendte af en funktion"
Оцените, пожалуйста статью
Populær