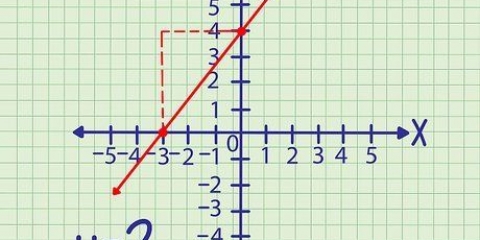
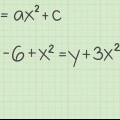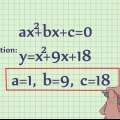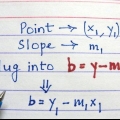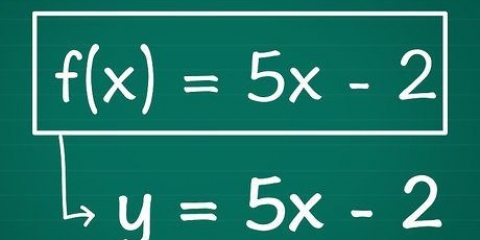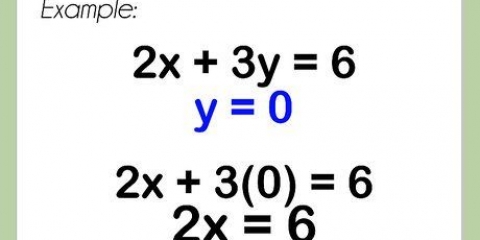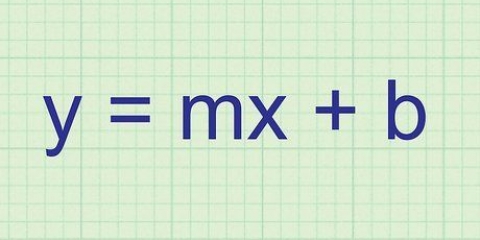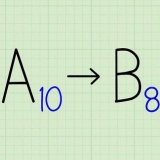For x = 2 er punktet på kurven (2,27) fordi f(2) = 2^3 + 2*2^2 + 5*2 + 1 = 27. For f`(x) = 3x^2 + 4x + 5, er hældningen inde (2,27) er f`(2) = 3(2)^2 + 4(2) + 5 = 25. 
I point-slope-formen er m skråningen og (x1,y1) er punktets koordinater. Så i dette eksempel bliver ligningen y - 27 = 25(x - 2). 
Find ligningen for en tangentlinje
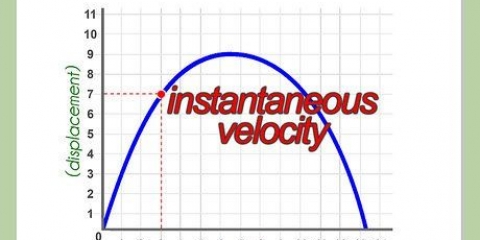
En tangent til en parabel eller kurve er en linje, der kun rører kurven i et givet punkt. For at finde ligningen for denne tangentlinje skal du beregne kurvens hældning på det punkt, hvilket kræver et par matematiske beregninger. Du kan derefter skrive ligningen for tangentlinjen i en punkthældningsform. Denne artikel forklarer de trin, du skal tage.
Trin

1. Ligningen for en kurve kan udtrykkes som en funktion. Find den afledede af denne funktion for at finde ligningen for hældningen af denne kurve.
- Den nemmeste måde at differentiere de fleste polynomier på er gennem kædereglen. Multiplicer hver ligning af funktionen med dens potens for at finde koefficienten for det led i den afledede, og subtraher derefter potensen med 1.
- Eksempel: For funktionen f(x) = x^3 + 2x^2 + 5x + 1 er den afledede f`(x) = 3x^2 + 4x + 5.
- For f(x) = (2x+5)^10 + 2*(4x+3)^5, er den afledte f`(x) = 10*2*(2x+5)^9 + 2*5*4 *(4x+3)^4 = 20*(2x+5)^9 + 40*(4x+3)^4.

2. Hvis alt er vel, angives koordinaterne, hvor tangentlinjen møder kurven. Indsæt x-værdien af dette punkt, i den afledede funktion, for at finde kurvens hældning på det punkt.

3. Denne hældning er også hældningen af tangentlinjen. Nu har du hældningen og punktet på denne linje, så du kan skrive linjens ligning på punkthældningsform, eller y - y1 = m(x - x1).

4. Det kan også være nødvendigt at konvertere denne ligning til en anden form for at få det endelige svar, hvis instruktionerne medfølger problemet kræver det.
Artikler om emnet "Find ligningen for en tangentlinje"
Оцените, пожалуйста статью
Populær